UA   EN
ДонНТУ   Портал магистров

Анализ и реализация модели конфигурационного взаимодействия для фуллеренов

Содержание

Введение

Проблема корректного учёта взаимодействия между электронами возникла уже в первые годы после создания квантовой механики [1 – 3], когда обнаружилась её тесная связь со спиновой степенью свободы электрона [4]. При этом от двух электронного её варианта, объяснившего природу ковалентной химической связи [5], до применений математического аппарата группы перестановок [6, 7], унитарного формализма [8 – 10] и до её подгрупп пространственной симметрии [11] сложность вычислительных схем экспоненциально росла. Кластерные подходы [12], открывающие возможность привлечения химической интуиции, тоже не решают проблему эффективного учёта мультиплетности состояния и симметрии его, включая пространственную, для изучения свойств сложных молекулярных систем.

Модель конечного автомата, предложенная Э. Муром в 1956 году и названная в его честь (автомат Мура), как синхронная последовательностная схема, является частью многих цифровых систем и применяется при построении устройств управления. Высокая сложность интегральных схем (которая продолжает повышаться, следуя закону Г. Мура) и теоретический базис автоматных вычислений делает возможной реализацию комплексных алгоритмов обработки информации. Однако, непосредственная реализация алгоритмов может приводить к неэффективному использованию ресурсов кристалла и увеличению стоимости проекта.

1. Актуальность темы

Открытие углеродного кластера в форме усечённого икосаэдра [13], а затем и трубчатых углеводородов [14] в 60–х и 70–х годах сначала было гениальным предвидением, не противоречивым для теоретической химии фактом. Но затем, в 80–х и 90–х годах, экспериментально [15, 16] были открыты новые соединения углерода, фуллерены и нанотрубки. “Ожидаемые” открытия этих соединений углерода с высокой пространственной симметрией, включая симметрию икосаэдра, оказались революционными и дали новое направление в нано технологиях. Они применяются во многих областях, включая медицину. Это делает актуальной проблему эффективного теоретического изучения их неожиданных, интересных для применений свойств таких нано структур.

Нанообъекты интересны, прежде всего, своими супрамолекулярными свойствами: динамикой ионов, атомов и молекул–гостей, а также способностью отдавать и принимать электроны в мягких условиях. С ними, в частности, связаны основные биологические функции белковых тел (электронный и протонный транспорт, подавляющее количество каталитических биохимических реакций). Характерно для углеродных наноструктур и то, что они способны выступать как в роли восстановителей, так и в роли слабых окислителей. В свою очередь, подобные свойства определяются электронной структурой объектов, которая имеет как общие черты, так и безусловные и яркие отличия. Квантовохимический подход к их изучению позволяет рассматривать эти два, на первый взгляд весьма различных, класса соединений (см. Рисунок 1), фуллерены и нанотрубки, как кластерный объекты из углеродных атомов, только разной пространственной симметрии.

В фуллерене пятиугольники формируют 30о положительное искривление плоскости шестиугольников (купол), а семиугольники могут дать, – 30о отрицательное искривление плоскости (внутренняя сторона «бублика», если его формировать из нанотрубки). Такие их искажения, могут вызвать появление полупроводниковой проводимости.

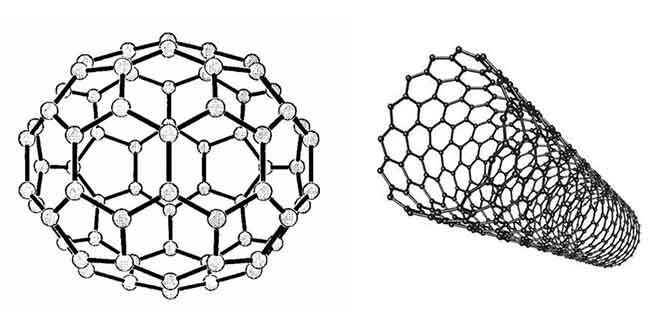
Модель молекулы фуллерена C60 и углеродной нанотрубки

Рисунок 1 – Модель молекулы фуллерена C60 и углеродной нанотрубки

Самый низший фуллерен С20 – правильный додекаэдр, состоящий из 12 пятиугольников, структура остальных фуллеренов обязательно содержит 12 пятиугольников и какое–то количество шестиугольников (в С60 их 20) (см. Рисунок 1). Поскольку особенностью атома углерода является его способность образовывать практически любые сложные объемные структуры, состоящие из многоугольников, то углеродные наноструктуры, из–за своих размеров, фактически служат переходным мостом между отдельными молекулами и кристаллами.

Электрические, оптические и механические свойства фуллеренов в конденсированном состоянии указывают на богатое физическое содержание явлений, происходящих при участии фуллеренов. Кристаллические фуллерены и пленки из них представляют собой полупроводники с шириной запрещенной зоны 1,2–1,9 эВ и обладают фотопроводимостью при оптическом облучении. Фуллерены в кристаллах характеризуются относительно невысокими энергиями связи, поэтому в них уже при комнатной температуре наблюдаются фазовые переходы, приводящие к ориентационному разупорядочению и размораживанию вращения молекул фуллеренов. Кристаллы С60, легированные атомами щелочных металлов, обладают металлической проводимостью и переходят в сверхпроводящее состояние в диапазоне от 19 до 55 К в зависимости от типа щелочного металла.

С открытием фуллеренов многие связывают возможный переворот в органической химии. Молекулы фуллеренов, в которых атомы углерода связаны между собой, как одинарными, так и двойными связями, являются трехмерными аналогами ароматических структур, например, С48 [17]. Обладая высокой электроотрицательностью, они выступают в химических реакциях, как достаточно сильные окислители. Присоединяя к себе радикалы различной химической природы, фуллерены способны образовывать широкий класс химических соединений, обладающих и его эндоэдральные комплексы уже синтезируемых в макроколичествах. В последнем один или несколько атомов металлов, неметаллов или даже отдельных молекул помещаются внутрь углеродной сферы. Ожидается, что на основе таких комплексов в будущем будут созданы высокоэффективные лекарства против рака.

Объяснение таких уникальных физических и химических свойств фуллеренов кроется, конечно, в особенностях их электронной и атомной структуры. Так, если в классических плоских ароматических структурах s – и р – связи геометрически ортогональны, то в фуллеренах и нанотрубках, за счет ненулевой кривизны их поверхностей, – нет.

Присоединение к С60 радикалов, содержащих металлы платиновой группы, позволяет получить ферромагнитный материал на основе фуллеренов. Новые химические свойства обнаруживают соединения, структура которых получается в результате замены части атомов углерода на металлы. К таким соединениям, называемым металлокарбонами, относятся, например, Ti8C12, V8C12, Hf8C12, Zr8C12. Стоит отметить, что магнитными свойствами обладает и фуллерен С28 [19].

Разнообразие физико–химических и структурных свойств соединений на основе фуллеренов позволяет говорить о химии фуллеренов, как о новом перспективном направлении органической химии. Его развитие может привести к непредсказуемым результатам [16, 18].

2. Цель и задачи работы

Целью данной работы является:

  1. Объединение разных методов самосогласованного поля, от одно конфигурационного до много конфигурационного взаимодействия, с учётом пространственной симметрии, например, фуллеренов и нанотрубок, при расчёте их электронных, магнитных и оптических свойств в едином подходе координатной функции Фока и матрицы плотности.
  2. Описание применения свойств унитарной, ортогональной и постранственной групп симметрии для выделения всех возможных состояний открытой оболочки высокосимметричной системы, содержащей до пяти вырожденных орбиталей неприводимого представления, например, группы икосаэдра, для которых возможно вычисление констант в функционале энергии и в вариационных уравнениях, отвечающих каждому её состоянию, и дать способ его реализации.
  3. Обзорное изложение, в том же едином подходе, достижений в решении вопроса о применимости молекулярных методов для расчёта атомов с открытыми оболочками.
  4. Создание единого программного продукта, объединяющего методы, применимые для расчётов электронных состояний фуллеренов, нанотрубок и фуллеритов с открытой оболочкой.
  5. Изучение характера сходимости итерационного процесса для решения уравнений, дающих оптимизацию молекулярных орбиталей и минимум энергии состояния, и изучение способов, дающих гарантированную сходимость процесса решения этих уравнений, а также и ускорение процесса самосогласования.

3. Научная новизна

3.1 Объекты исследования

В 90–е годы были разработаны методы синтеза фуллеренов в макроколичествах [20] и найдены способы их разделения и очистки [21, 22]. Кроме того, были определены важнейшие структурные и физико–химические характеристики С60 (Рисунок 1) – наиболее распространенного представителя этого класса веществ. К настоящему времени опубликовано более 10 000 работ по фуллеренам, в том числе и ряд обзоров [23 – 21]. Проводимые исследования охватили такие, казалось бы, далекие друг от друга области науки, как астрономия и органическая химия, физика твердого тела и медицинская биология, неорганическая химия и геометрия. Фуллерены относят одновременно и к неорганическим материалам – как новые аллотропные модификации углерода, – и к органическим соединениям, поскольку в химических превращениях они проявляют многие свойства непредельных углеводородов.

В настоящее время фуллерены стали предметом интенсивных исследований большого числа научных групп, за результатами которых пристально наблюдают прикладные компании (на Западе такие крупные, как Exxon, Du Pont, АТ & Т из США, NEC из Японии, Hoechst АG из Германии и др.). В 1993 г. начал издаваться журнал Fullerene Science and Technology, посвященный фуллеренам и имеющий в названии слово «технология» (в число его издателей вошли и будущие нобелевские лауреаты, Robert F. Curl, Harold W. Kroto, Richard E. Smolley [30]).

Фуллерены, как оказалось, связаны с историей развития Земли и Солнечной системы.

Фуллерены входят в состав земной коры, стало известно уже после их открытия. Правда, содержание их невелико и распределены они весьма неравномерно, поэтому химические исследования земных фуллеренов вряд ли сегодня можно считать полными. Природные фуллерены найдены в некоторых минералах. Соотношение С60:С70 в них меняется в интервале 0,21–0,36 [31]. Предполагают, что фуллерены способствуют миграции и концентрации ряда элементов, в частности, оказывают влияние на формирование месторождений алмазов и являются катализатором для их синтеза.

Как и когда фуллерены образовались в толще земных пород? Чёткого понимания этого пока нет, тем более что пути их образования могут быть самыми разными. Л. Беккер с коллегами изучили изотопный состав инертных газов, захваченных фуллеренами при их образовании и сохранившихся внутри прочной углеродной оболочки. Образцы природных пород с фуллеренами С60 – С200 были взяты из разных точек нашей планеты: они были найдены геологами в Японии, Китае и Венгрии. Европейские образцы оказались малоинтересными, а азиатские содержали относительно большую концентрацию фуллеренов. Согласно результатам Беккер [32], некоторые фуллерены были заполнены: внутри оболочек находились атомы гелия. При этом обнаружились странности: фуллерены хранили не гелий–4 – изотоп, который обычно присутствует в земных породах, – а редкий для Земли изотоп гелий–3. Раньше Беккер нашла фуллерены в местах падения метеорита в Сандбери (провинция Онтарио, Канада) и астероида Альенде в Мексике около 30 лет назад. Возраст последнего насчитывает 4,6 млрд лет.

Открытие позволило установить, что такие фуллерены могли образоваться только в космических условиях в так называемых углеродных звездах или в ближайшем их окружении. Беккер пояснила [32], что необычайно высокие температуры и давления в этих звездах «возможно, дают единственный путь, по которому можно заставить космические благородные газы внедриться внутрь фуллеренов». Речь, надо полагать, идет о взрыве звезды, который произошел задолго до появления Солнечной системы.

Удалось определить и время появления исследованных фуллеренов на Земле. Кратер от падения канадского метеорита образовался 1,85 млрд. лет назад, в архейскую эру, когда Земля еще была безжизненна, «безвидна и пуста». Другие фуллерены появились гораздо позже. Поскольку они были обнаружены на границе отложений пермского и триасового периодов, их возраст оценен в 250 млн. лет. Именно тогда в Землю врезался грозный космический гость, который долго скитался по своим орбитам, – гигантский астероид или ядро кометы, вызвавший катастрофические разрушения. Эта катастрофа, как предполагают, была более страшной, чем удар астероида, произошедший 65 млн. лет назад, на границе мелового и третичного периодов. На память о себе астероид распылил принесенные им фуллерены и иридий [33].

Принято считать, что наиболее богаты фуллеренами шунгитовые породы. Громадные залежи шунгита пока обнаружены лишь в одном месте – в Карелии, недалеко от деревни Шуньга. Именно в карельских шунгитах были впервые открыты земные фуллерены. Один из бывших советских ученых исследовал в Аризонском университете (США) образцы шунгитов, взятые из российского Геологического института, и, к удивлению всего научного сообщества, обнаружил там углеродные глобулы с фуллеренами. После сенсационного сообщения об этом и начался интенсивный поиск других пород, содержащих фуллерены, возникли вопросы об их происхождении на Земле.

Сейчас с наличием в шунгитах фуллеренов некоторые энтузиасты связывают целебное действие открытых в 1714 г. марциальных вод, которыми лечился Петр Великий. Есть предположения, что к молекулам фуллеренов в шунгитах присоединены какие–то органические радикалы, которые позволяют фуллеренам образовывать водные растворы с концентрацией до 30–50 мг/л. Правда, более тщательные исследования показали, что одни месторождения шунгитов действительно содержат фуллерены, в то время как другие – лишь сажистые вещества.

4. Обзор существующих и развиваемых методов

4.1. Ограниченный метод Хартри–Фока

Этот метод описан как метод открытых оболочек в [34]. Он является очевидным обобщением метода самосогласованного поля, используемого для расчета основных состояний атомов и молекул. В качестве волновой функции используется один детерминант, в котором q орбиталей занято двумя электронами со спинами α и β, тогда как ρ – q орбиталей занято одним электроном со спином α, т.е.:

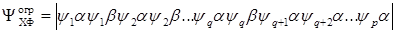
Формула 1

Можно найти уравнения, аналогичные уравнениям Хартри–Фока, из которых затем определяются орбитали Формула 2, необходимые для минимизации энергии, соответствующей Формула 3. Эти уравнения были впервые выведены Леннард–Джонсом. Они более сложны, чем обычные уравнения Хартри–Фока, поскольку их нельзя просто свести к виду задачи о собственных значениях. Однако Мак–Вини и Рутан развили методы решения этих уравнений [35]. Для орбиталей в неортогональном базисе гауссовского или Слейтер типа их можно записать в виде напоминающей обобщенную задачу на собственные значения, хотя они не являются стандартной задачей на собственные значения, так как они являются нелинейными:

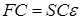
Формула 4

где F – матрица Фока (которая зависит от коэффициентов C за счет электронных взаимодействий), С представляет собой матрицу коэффициентов, S является матрицей перекрывания базисных функций, ε – энергии орбиталей. В случае ортонормированного базиса матрица перекрывания, S, сводится к единичной матрице. Эти уравнения по существу являются частным случаем метода Галеркина.

4.2 Неограниченный метод Хартри–Фока

Ограниченный Метод Хартри–Фока нельзя применять для систем с открытыми (незамкнутыми) оболочками: радикалы (один неспаренный электрон), триплетные и синглетные возбужденные состояния молекул (два неспаренных электрона), многие органические и неорганические комплексы переходных металлов (несколько неспаренных электронов, заселяющих вырожденные d– или f–орбитали), изолированные атомы с незаполненными оболочками. Метод нахождения волновой функции, аналогичный методу ОХФ, при котором пространственные части одноэлектронных спин–орбиталей варьируются независимо, называется неограниченным методом Хартри–Фока (НХФ, UHF) [36].

Получаемые выражения для оператора Фока и энергии сходны с выражениями ограниченного метода ХФ, однако уравнения Хартри–Фока–Рутана распадаются на две взаимосвязанные системы уравнений, соответствующие электронам с противоположными спинами:

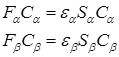
Формула 5

Процедура самосогласования остается аналогичной методу ОХФ, однако получаемые решения имеют особенности, отличающие их от решений ОХФ.

  1. Коэффициенты МО электронов с разными спинами Сijα и Сijβ не одинаковы.
  2. Когда количества электронов с противоположными спинами не равны, различными оказываются и энергии спин–орбиталей εα и εβ.

Главное преимущество метода НХФ в возможности описания систем с неспаренными электронами и его простота, поскольку алгоритм расчета, как и структура программ, аналогичны методу ОХФ. В настоящее время, подавляющее большинство квантовохимических программ включают модули, позволяющие находить решения методом НХФ.

4.3 Ограниченный метод Хартри–Фока для открытой оболочки

Отмеченные выше недостатки НХФ метода частично удается решить с помощью «ограниченного метода Хартри–Фока для открытой оболочки» (ОХФО, Restricted Open–shell Hartree–Fock method, ROHF), в котором замкнутые и открытые оболочки описываются по–разному. Замкнутые оболочки состоят из дважды занятых орбиталей; их расщепление не предполагается. Но в зависимости от природы открытой оболочки, её волновая функция может быть одним детерминантом, как в случае дублета или высокоспиновых компонент триплета (Sz = 1 или Sz = -1), или же она может быть линейной комбинацией двух и более детерминантов.

В схеме ОХФО разные открытые оболочки описываются по единой схеме на основе достаточно общего выражения для энергии, содержащего численные коэффициенты, значения которых отличаются для разных состояний. Во всех случаях предполагается, что мы имеем дело с некоторым числом N ортонормированных (пространственных) орбиталей, φi, каждой из которых можно сопоставить свое число заполнения ωi, и электронную энергию записать, как:

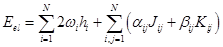
Формула 6

где «коэффициенты связи», αij и βij определяются типом состояния с открытой оболочкой (т.е. для каждого типа открытой оболочки – дублета, триплета и т.д. выбираются соответствующие константы α и β). Когда эти коэффициенты зависят от номера орбитали открытой оболочки, термы называют нерутановскими [40], а в случае независимости их от номера орбитали – рутановскими [41].

Для определения ВФ можно использовать обычную процедуру вариации электронной энергии с применением метода множителей Лагранжа, тогда в результате вариации получаются уравнения Эйлера. Система этих уравнений распадается на совокупность N уравнений, так называемых «k–зависимых» операторов Фока ОХФО, т.е. для каждой орбитали или для каждого класса орбиталей имеется свой оператор Фока:

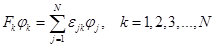
Формула 7

Часто удобнее записать систему уравнений в виде одного уравнения. Чтобы это сделать, вводят единый связывающий оператор (unified coupling operator), который объединяет все уравнения, причем получаемые затем уравнения оказываются идентичны уравнениям Хартри–Фока и решаются аналогичным образом путем самосогласования. Наиболее естественным способом такие объединения получаются применением метода матрицы плотности [39].

  1. В целом метод ОХФО дает более правильное описание ВФ открытых систем, чем метод НХФ, поскольку его ВФ изначально обладает правильной спиновой симметрией. Исключение составляют явления спиновой поляризации, о которых говорилось в предыдущем разделе.
  2. Наибольшее преимущество этот метод демонстрирует при описании вырожденных и высокоспиновых систем, для которых НХФ и другие методы, за исключением КВ и МК ССП, непригодны, дают не симметричные решения.
  3. Недостатками данного метода является и необходимость «ручного» задания коэффициентов ωi, αij, βij для различных типов вырожденных состояний, а также то, что большинство используемых программ применяют единые связывающие операторы, не воспроизводящие теорему Купманса. Оригинальный метод вычисления таких коэффициентов для всех рутановских термов в аналогичном подходе предложен в [41].
  4. Точность оценки многих молекулярных свойств в случае низко спиновых и невырожденных систем с открытой оболочкой (радикалы, невырожденные триплеты), а также систем с замкнутыми оболочками не может конкурировать с точностью более сложных (и громоздких) методов: MPn, DFT, CCSD и QCISD.

4.4 Метод матрицы плотности и координатной функции Фока

В Институте физико – органической химии и углехимии НАН Украины (г. Донецк) изучались свойства матрицы плотности [38]. Решались также проблемы квантовой механики без спина построением и координатных функций Фока, и пространственных компонент матрицы плотности для состояний многоэлектронной системы с определённым полным спином [42, 43] применением симметрической группы [6]. Метод матрицы плотности применялся и для записи уравнений Хартри – Фока – Рутана в форме удобной и для исследования свойств метода, включая и вопросы его нестабильности [39], и для изучения свойств молекул. Применением базисов унитарной и ортогональной групп Формула 8 был предложен универсальный способ вычисления постоянных коэффициентов в уравнениях Хартри – Фока – Рутана [40, 41], которые применены, например, в расчётах рутановских термов фуллеренов с открытой оболочкой [19, 44]. Отметим подробнее теоретические основы для применяемых методов.

В.А. Фок в [45, 46] записал волновую функцию ΨsM со спином s и его проекцией M:

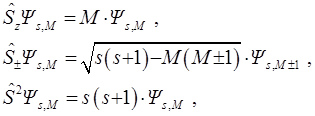
Формула 9

в виде, содержащем явное отделение функции пространственных координат Фs или функции Формула 10 со знаковым множителем. Последняя удобная в применениях метода Фока:

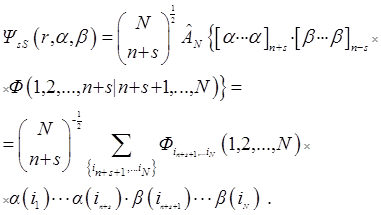
Формула 11

Как и в [40, 41], координаты частиц обозначены их номерами, Формула 12 – антисимметризатор, спиновые функции α и β ортонормированные и Формула 13Формула 14.

Тождества гарантируют три условия Фока для Фs [45]. Это её антисимметрия:

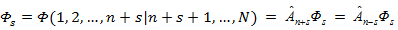
Формула 15

в каждом наборе переменных, разделенных чертой, и условие циклической симметрии, запрещающее антисимметризацию Фs по n+s+1–ой частицам,

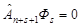
Формула 16

Черту в функции Фока Фs вправо сдвигать нельзя. Её “смещение” влево даёт координатные функции ФsM = Ф(1, 2,…, n+M|n+M+1,…, N) состояний ΨsM. Сдвиг черты влево более, чем на 2s координат, снова запрещен условием циклической симметрии функции Фока [34].

Координатную функцию Фока можно строить для разных приближенных методов: от метода Хартри – Фока – Рутана [41] до координатной функции метода полного конфигурационного взаимодействия в [47].

Удобный алгоритм их применения основан на общей для всех приближений связи плотностей координатных функций Фока Фока Фs = Ф(1, 2, …, n+s|n+s+1,…, N) соответствующей частичности, вычисляемых для каждого приближения отдельно:

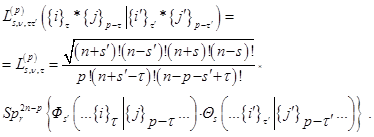
Формула 17
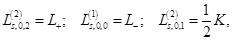
Формула 18

с применяемыми в приложениях одночастичными: зарядовой, Формула 19, и спиновой ds плотностями

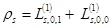Формула 20;
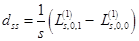Формула 21,

и с двухчастичными, – пространственной, R, спин–орбитальной, D, и спин–спиновой, F, плотностями:

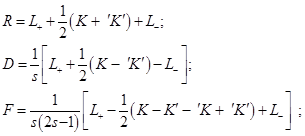
Формула 22

Здесь ν = s′– s = τ – τ′, и пространственные не штрихованные и штрихованные координаты частиц, стоящие до и после черты в функциях Формула 23 и Формула 24, указаны их номерами: Формула 25Формула 26 и Формула 27. Штрихи слева и/или справа от R, D и F обозначают перестановки их штрихованных и/или нештрихованных координат.

Координатная функция Фока для квазипинового мультиплета, усреднение по которому, как выяснилось, и является тем минимальным базисом, что даёт Рутановские термы, строятся редукцией базиса функций Фока унитарной группы, Формула 28, до неприводимого базиса её ортогональной подгруппы, Формула 29 [41].

Гамильтониан многоэлектронной системы с открытой оболочкой в таком методе имеет предложенную Рутаном [34, 35] форму, которая существенно откорректирована для описания “усредненного квазиспинового мультиплета” в работе [41] на основе идей Рака [48]:

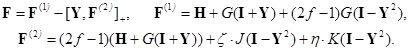
Формула 30

Здесь, I + Y – зарядовая и порядков связи матрица плотности, I – Y2 является тем же самым для открытой оболочки, F – единый оператор Фока этого метода, H – матрица энергии ядерного остова, J и K – линейные матричные операции, описывающие кулоновское и обменное взаимодействия, действующие на зарядовое распределение, обозначенное в скобках, и G = J + K. Оптимизированные орбитали (или матрица Y) и энергия Eξη, характеризующие усредненный квазиспиновый мультиплет, могут быть найдены из матричных уравнений самосогласованного поля (ССП):

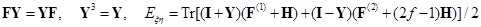
Формула 31

записанных в применяемом атомном базисе. Числовые константы f, ζ и η зависят от числа электронных пар n (n может быть полуцелым) в открытой оболочке, от степени вырождения m, включая случайное их вырождение, от спина s, и от числа старшинства ν, ν = s, …, n.

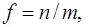
Формула 32
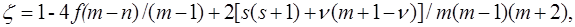
Формула 33
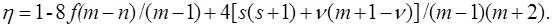
Формула 34

Подробности применяемых при выводе методик можно найти в статье [41].

5. Задачи, решаемые при создании единого программного пакета

В едином подходе координатной функции Фока и матрицы плотности разработать программный продукт, в котором необходимо:

  1. Реализовать ограниченный метод Хартри – Фока – Рутана с автоматическим выбором или вычислением коэффициентов нужных для функционала энергии и фокиана, чтобы эффективно учесть ограниченное конфигурационное взаимодействие для открытой оболочки каждого рассчитываемого состояния.
  2. Проектированием плотности открытой оболочки на орбитальное подпространство определённой симметрии, гарантировать сохранение в процессе расчёта определённого заполнения самосогласованных вырожденных орбиталей.
  3. Приспособить метод проектирования для расчёта возбуждённых состояний.
  4. Реализовать ограниченное конфигурационное взаимодействия для расчёта мультиплетных состояний нанотрубок и фуллеренов так, чтобы при наличии случайного вырождения граничных орбиталей была возможность сохранить это вырождение в процессе самосогласования.
  5. Для гарантированной сходимости итерационного метода решения аналогичных ССП уравнений и ускорения процесса самосогласования изучить применимость методик «масштабирования» [51 – 53].
  6. Оценить эффективность ограниченного конфигурационного взаимодействия при расчёте фуллеренов и нанотрубок, и средствами существующего программного языка, по возможности, графически отобразить структуру углеродного кластера, распределения в нём зарядовых и спиновых плотностей.

При разработке отдельного программного продукта выполняются задачи, указанные выше. Пользователю будет предоставлена возможность посредством использования интерфейса пакета провести расчёты разных состояний углеродного кластера с открытой (или замкнутой, как частный случай) оболочкой и оценить роль конфигурационного взаимодействия для определения, в итоге, его основного и возбуждённых электронных состояний.

Выводы

В этой магистерской диссертации обоснована актуальность и новизна решаемых задач. Объектом исследования выбран перспективный для практических применений новый класс соединений – фуллерены и нанотрубки. Обозначены многообразие их объёмных форм и обилие соединений, синтезируемых на их основе, выявления полезности применения свойства, в том числе и в медицине.

Поставленные цели и задачи данной дипломной работы указаны выше.

Не решёнными, но важными для совершенствования развиваемого метода, остаются:

  1. Вопрос о возможной причине наличия у высокосимметричных молекулярных систем случайного вырождения, как у атомов с d–оболочкой [49, 50], и условия его снятия с сохранением симметрии кластера.
  2. Исследовать при наличии у вырожденного состояния системы с открытой оболочкой оси симметрии третьего порядка возможности появления для него универсальной нестабильности, то есть перехода системы в стабильное самосогласованное состояние с нарушением симметрии.
  3. Возможность сохранения преимуществ алгоритма вычисления рутановских состояний, усреднённых по квазиспиновому мультиплету, при создании эффективного метода расчёта чистого по пространственной симметрии состояния так, как, например, в расширенном по спину методе Хартри – Фока.

Замечание

Реферат составлен до завершения работы, и возможны изменения до конца оформления магистерской диссертации.

Список источников

  1. E. Schrodinger. Quantisierung als Eigenwertproblem (Erste Mitteilung) // Annalen der Physik. – 1926. – Vol. 384 (79). – P. 361 – 376. Русский перевод: Э. Шрёдингер. Квантование как задача о собственных значениях (первое сообщение) // УФН. – 1977. – Т. 122. – С. 621 – 632.
  2. W. Heisenberg. Uber quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen // Zeitschrift fur Physik. – 1925. – Vol. 33, № 1. – P. 879 – 893. Русский перевод: В. Гейзенберг. О квантовотеоретическом истолковании кинематических и механических соотношений // УФН. – 1977. – Т. 122, вып. 8. – С. 574 – 586.
  3. W. Heisenberg. Uber den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik // Zeitschrift fur Physik. – 1927. – Vol. 43, № 3 – 4. – P. 172 – 198. Русский перевод: В. Гейзенберг. О наглядном содержании квантовотеоретической кинематики и механики // УФН. – 1977. – Т. 122, вып. 8. – С. 651 – 671.
  4. Dirac P.A.M. The Quantum Theory of the Electron // Proc. Roy. Soc. (London), 1928, V. 117, P. 510 – 624. The Quantum Theory of the Electron (part II) // Proc. Roy. Soc. (London), 1928, V. 118, P. 351 – 361.
  5. Heitler W., London F. Wechselwirkung neutral Atome und homoopolare Bindung nach der Quantenmechanik. // Z. Phys., 1927, Bd 44, S. 455 – 472.
  6. Хаммермеш М. Теория групп и её применение к физическим проблемам – Москва: Мир, 1966. – 587 с.
  7. Каплан И.Г. Симметрия многоэлектронных систем. – Москва: Наука, 1969. – 407 с.
  8. Shavitt I. Graph Theoretical Concepts for the Unitary Group Approach to the Many – Electron Correlation Problem // Int. J. Quantum. Chem., 1977. S. 11. P. 131 – 148.
  9. Shavitt I. Matrix Element Evaluation in the Unitary Group Approach to the Electron Correlation Problem // Int. J. Quantum. Chem., 1978. S. 12. P. 5 – 32;
  10. Климко Г.Т., Лузанов А.В. Решение проблемы определения спиновых свойств молекул в унитарном формализме квантовой химии. // Журн. Структурн. Химии. – 1987. – т. 28, № 5. – с. 3 – 9.
  11. Вигнер Е. Теория групп и её приложения в квантовомеханической теории атомных спектров. – Москва: И.Л., 1961. – 443 с.
  12. Luzanov A.V. Matrix–Covariant Representation of High–Oder Configuration Interaction and Coupled Claster Theories // Int. J. Quantum. Chem., 2008, V. 108, N 4. P. 671 – 695.
  13. Бочвар Д. А., Гальперн Е.Г. Электронная структура молекул С20 и С60 // ДАН СССР Серия химическая. 1973. Т. 209, №3. С. 610–615.
  14. Корнилов М.Ю. Структура и свойства трубчатых углеводородов / М.Ю. Корнилов // Доклады АН УССР, серия «Б». – 1977. – Т.12. – с. 1097 – 1102.
  15. Кrotto H.W. Struсture of C60 moleсule / H.W. Кrotto // Nature. – 1992. – V. 358. – Р. 220 – 225.
  16. S. Iijima, Helical microtubules of graphitic carbon // Nature, – 1991, – V. 354. P. 56
  17. Структура, хартри–фоковская стабильность, антисимметричные решения, спектры основного и ионизированного состояний альтернантного архимедова тела С48 / Местечкин M.M., Климко Г.Т., Вайман Г.Е., Паничкина В.А. // Журн. структ. химии. – 1992. – Т. 33, №2. – С. 8 – 14. (J. Struct. Chem. – 1992. – V. 33, № 2. – p. 161 – 166, (translated from Russian).)
  18. Кузубов А.А. Электронная и атомная структура изомеров эндо– и экзоэдральных комплексов фуллеренов с двумя атомами лития / А.А. Кузубов. П.В. Аврамов, С.Г. Овчинников, С.А. Варганов, Ф.Н. Томилин // ФТТ. – 2001. – Т. 43. – с. 1721–1726.
  19. Mestechkin M.M., Klimko G.T. C28 is fullerene with possible quintet ground state // Mol. Mat. C. – 1996. – Vol. 8. – P. 165 – 168.
  20. Huffman D.R., Кraetschmer W., Lamb L.D., Fostjroрoulos К //Nature. 1990. V.347. P.354–358
  21. Вaun R.M. //Chem. Eng. New. 1985. V. 63. 1 51. P.20–29.
  22. Тaylor R., Hare J.P., Аbdul–Sada А.К., Кroto H.W. //J. Chem. Soc., Chem. Commun. 1990. P. 1423–1431
  23. Сидоров Л.Н., Болталина О.В. //Успехи химии. 2002. Т.71. 17. С.611–640.
  24. Соколов В.И., Станкевич И.В. //Успехи химии. 1993. Т.62. №5. С.455–472.
  25. Дикий В.В., Кабо Г.Я. //Успехи химии. 2000. Т.69. № 2. С.107–117.
  26. Елецкий А.В. //Успехи физических наук. 2000. Т.170. № 2. С.113–129.
  27. Караулова Е.Н., Багрий Е.И. //Успехи химии. 1999. Т.68. №11. С.979–998.
  28. Конарев Д.В., Любовская Р.Н. //Успехи химии. 1999. Т.68. №.1. С.23–44.
  29. Мюллер А., Рой С. //Успехи химии. 2002. Т.71. №12. С.1107–1119.
  30. EDITORIAL Diagnosis of the Fullerene Fever on the Occasion of the 1996 Nobel Prize in Chemistry // Fullerene science and technology, V. 5, N 1, P. iii – v.
  31. Винокуров С.Ф., Новиков И.Н., Усатов А.В. //Геохомия. 1997. С.937–940.
  32. Вecker L., Poreda R.J., Hunt А.J., Вunch Т.E., Ramрjno M. //Scjence. 2001. Т.291. С.1530–1533.
  33. Масайтис В. Л. //Региональная геология и металлогения. 1993. №1. С.121–125.
  34. Roothaan C. C. J. Self–Consistent Field Theory for Open Shell Electronic Sistems // Rev. Mod. Phys., 1960. – V. 32, N 1. – P. 179 – 186.
  35. Roothaan C. C. J., Hinze I. Multi–configurational selfconsistent field theory. // Progr. Theor. Phys.Suppl., 1967, V. 40, P. 35 – 50.
  36. Fukutome H. Theory of the unrestricted Hartree – Fock equation and its solutions. // Prog. Theor. Phys., 1974, – V. 52, N 1. – P. 115 – 130; N 6. – P. 1766 – 1783; 1975, – V. 53, N 5. P. 1320 – 1336.
  37. Mestechkin M.M., Whyman G.E. Matrix Formulation of the Generalized Hartree – Fock Methods // Int. J. Quantum Chem., 1974, V. 8 N 1. P. 45 – 60.
  38. Местечкин М. М. Метод матрицы плотности в теории молекул. Киев: Наук. Думка, 1977. – 352 с.
  39. Местечкин М. М. Нестабильность уравнений Хартри–Фока и устойчивость молекул. Киев: Наук. Думка, 1986. – 176 с.
  40. The Origing of Energy Functional in Roothaan Open Shell RHF Theory / Klimko G.T., Mestechkin M.M., Plakhutin B.N., Zhidomirov G.M. // Int. J. Quantum. Chem. – 1990. – V. 37, № 1. – P. 35 – 50.
  41. Klimko G.T., Mestechkin M.M. Roothaan’s Open Shell Theory from the Viewpoint of an Orthogonal Group. // Int. J. Quantum. Chem. – 1990. – V. 37, № 5. – P. 753 – 771.
  42. Mestechkin M.M., Klimko G.T. Spin–dependent operators in the spin–free quantum chemistry // Intern. J. Quantum Chem. – 1978. – V. 13, № 5.–P.579–596.
  43. Klimko G.T., Mestechkin M.M., Whyman G.E. Fock coordinate function method for separation of spin variables in transition density matrices // Intern. J. Quantum Chem.–1980. – V. 17, № 3. – P. 415 – 428.
  44. Mestechkin M., Whyman G., Klimko G. Nonlinear optical properties of alternant fullerene C48 // Fullerene science and technology, 1997. – V. 5, N 1, P. 195 – 203.
  45. Фок В.А. О волновых функциях многоэлектронных систем // Журн. Эксперим. и теорет. физ. – 1940. – Т. 10, № 9 – 10. – С. 961 – 979.
  46. Фок В.А. Начала квантовой механики. – М.: Наука, 1976. – 376 с.
  47. Климко Г.Т., Местечкин М.М. Суперпозиция конфигураций и метод координатной функции Фока. // Многоэлектронная задача в квантовой химии (Сб. научных трудов), Наук. Думка, Киев. – 1987. – с. 31 – 43.
  48. Rakah J. Theory of Complex Spektra. IV. // Phys. Rev., 1949. – V. 76, N 9. – P. 1352 – 1365.
  49. Климко Г.Т. О применимости молекулярных методов для расчета атомов с открытыми оболочками. // Журн. физич. химии. – 1996. – т. 70, № 4. – с. 667 – 674.
  50. Климко Г.Т. К проблеме случайного вырождения термов в d– оболочке. // Журн. физич. химии. – 1999. – т. 73, № 3. – с. 507 – 512.
  51. Фаддеев Д. К. Вычислительные методы линейной алгебры / Д. К. Фаддеев, В. Н. Фаддеева. – Санкт–Петербург: Лань, 2002. – 736 с.
  52. Баркалов К.А. Методы параллельных вычислений/ К.А. Баркалов. –Н.Новгород: Изд–во Нижегородского университета им. Н.Лобачевского, 2012. – 124 с.
  53. Бахвалов Н.С. Численные методы / Н. С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. – Москва: БИНОМ. Лаборатория знаний, 2008. – 636 с.