Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Сверточные сети
- 3. Математическая модель АД.
- 4. Результаты моделирования АД.
- 5. Сверточная нейронная сеть
- Список источников
Введение
В настоящее время приводные системы на базе электродвигателей переменного тока играют ключевую роль в промышленном применении. Подсчитано, что на эти машины приходится примерно 29% мирового и 69% промышленного потребления электроэнергии. При эксплуатации электродвигателей в системах промышленного привода могут возникать различного рода дефекты, препятствующие дальнейшей эксплуатации машины. Согласно статистике, наиболее распространенными дефектами электрических машин являются повреждения статора (37%), ротора (10%) и подшипника (41%). Проведенные статические испытания показывают, что с увеличением номинальной мощности электродвигателей роль механических повреждений в пользу электрических уменьшается. Этот факт обусловливает то, что многие научные центры сосредоточены на разработке диагностических методов, позволяющих частично уменьшить количество электрических повреждений или выявить состояние машины (зарождающуюся неисправность), при котором она еще может быть отремонтирована.
Основой для работы диагностических систем является доскональное знание изменений, происходящих в машине в результате повреждения. Наблюдение за изменениями, происходящими в машинах переменного тока, осуществляется с помощью сигналов, доступных для измерения на исследуемом объекте. Наиболее часто используются токи, напряжения, вибрации, а также поток и температура. Идея аналитических методов оценки технического состояния машины основана на выделении признаков повреждения в измеряемых диагностических сигналах.
Использование аналитического подхода в процессах обнаружения неисправностей электрических обмоток двигателей переменного тока связано с необходимостью корректировки параметров измерения диагностического сигнала на метод выделения признаков неисправности. Используемые в настоящее время аналитические методы обнаружения повреждений основаны на наблюдении изменений сигнала во временной, частотной или чачтотно-временной области. Среди них особого внимания заслуживают следующие методы: быстрое преобразование Фурье (БПФ), расширенный векторный анализ парка, кратковременное преобразование Фурье, преобразование Гильберта-Хуана, а также вейвлет–анализ в виде непрерывного вейвлет-преобразования или дискретного вейвлет-преобразования. Из представленных методов наиболее распространенным является использование анализа БПФ. Анализ спектра сигнала обеспечивает как эффективную оценку симптомов повреждения, так и не создает значительной нагрузки на вычислительные системы. Однако, как и большинство аналитических методов, БПФ требует относительно длительного времени измерения, что, особенно в случае меж оборотных коротких замыканий обмотки статора, является несомненным недостатком данного метода, обусловленным динамикой этих неисправностей. Кроме того, во многих случаях невозможно обеспечить стационарность сигнала в течение требуемого периода измерения.
Распознавание изменений диагностических сигналов и их оценка в системах, основанных на аналитических методах, обычно выполняются человеком, что увеличивает время обнаружения неисправностей. Более того, такие системы часто не полностью автоматизированы, и количество ошибок часто связано с опытом человека-эксперта.[3-4]
1. Актуальность темы
В настоящее время в связи с динамичным развитием методов искусственного интеллекта диагностические системы, основанные на аналитических методах, постепенно заменяются нейронными детекторами повреждений. Несомненным преимуществом таких систем является ограниченная роль человека-эксперта в процессе оценки технического состояния объекта, обеспечивающая при этом высокую эффективность обнаружения неисправностей. Основой функционирования диагностических систем на основе нейронных сетей (ННС), применяемых также для обнаружения и классификации неисправностей асинхронных двигателей, являются аналитические методы. Поэтому входная информация для таких систем является результатом извлечения симптомов из выбранных диагностических сигналов с использованием аналитических методов.
Многослойные нейронные сети являются наиболее популярными структурами, используемыми в диагностических методах, в том числе в случае обнаружения неисправностей асинхронных и синхронных двигателей. Помимо возможностей аппроксимации данных, особенно важной задачей диагностических систем на основе нейросетей является классификация повреждений. Основным представителем классификаторов, используемых в процессах обнаружения неисправностей, является самоорганизующаяся сеть Кохонена. Преимуществом некоторых из них является его простая структура и тот факт, что нет необходимости обеспечивать несколько обучающих выборок.
Методы искусственного интеллекта все чаще ассоциируются с проблемой глубокого обучения. В основе структур глубокого обучения лежат классические нейронные сети. Однако глубокие нейронные сети (ГНН) характеризуются особенностями, отличными от классических неглубоких сетей, что является результатом отказа от универсального правила аппроксимации. Используемые до сих пор структуры, имеющие максимум два скрытых слоя, позволили достичь удовлетворительных результатов. Тем не менее, увеличение структуры позволило получить признаки нейросетей, которые ранее были недостижимы в классических неглубоких структурах.
Долгое время ГНН использовались в основном в информационных системах (например, обработка изображений, распознавание речи). За последнее время наблюдается растущий интерес к системам обнаружения повреждений электрических машин на базе ГНН. В большинстве случаев они связаны с анализом механических повреждений или механических компонентов системы. Небольшое количество работ, связанных с электрическими повреждениями им, в основном касаются повреждений ротора. Большинство систем на основе ГНН используют измерения вибрации, реже токов статора и напряжений. Этот факт вытекает из явных изменений, происходящих в диагностируемом сигнале, обусловленных механическим повреждением и вытекающей из этого простотой анализа сигнала.[1-2]
2. Сверточные сети
Среди используемых сетевых структур глубокого обучения наиболее часто используются сверточные нейронные сети (СНС). СНС, используемые в диагностических приложениях, характеризуются значительно более высоким уровнем эффективности по сравнению с другими сетями. В диагностических процессах СНС может выступать в качестве системы классификации повреждений, а также предоставлять информацию о степени повреждения. Важным аспектом при использовании ГНН в диагностических процессах является соответствующая настройка измеряемого сигнала на структуру и свойства сети. Входной вектор ГНН может быть получен в результате анализа сигнала и непосредственно предоставленного диагностического сигнала. Благодаря принципу работы структур глубокого обучения, в большинстве случаев измеряемый сигнал преобразуется в 2D или 3D матрицу.
В данной работе представлена возможность использования СНС в процессе обнаружения несиметрии фаз. Разработанное приложение характеризуется прямой обработкой необработанного диагностического сигнала. Здесь признаки повреждения извлекаются непосредственно из сигналов фазного тока статора, опуская хорошо известные аналитические методы предварительной обработки, такие как БПФ, вейвлет и другие преобразования более высокого порядка.
Описана идея диагностической системы на базе СНС, выполняющей задачу обнаружения неисправностей и оценки степени несиметрии обмоток статора АД. В отличие от методов, основанных на простом анализе вибрационного сигнала для обнаружения механических повреждений, разработанный метод заключается в прямой обработке сигналов фазного тока через ГНН, что является одним из новых подходов в системах обнаружения неисправностей статора.
Следует подчеркнуть, что разработка диагностической системы, основанной на прямом анализе тока статора, сопряжена с дополнительными трудностями, связанными с тем, несиметрия напряжений и повреждение обмотки вызывает аналогичный эффект, как и увеличение момента нагрузки, то есть увеличение амплитуды тока статора. Однако диагностическая система должна выявлять характеристики повреждения, то есть различать влияние несиметрии и влияние условий работы привода на анализируемый диагностический сигнал. [5]
Основная функция СНС заключается в извлечении признаков высших порядков из анализируемого сигнала с помощью сверточных операций. Эти сети не имеют заранее определенной архитектуры, методов выбора параметров или правил, касающихся количества сверточных слоев.
Структуру СНС следует рассматривать как определение признаков, которые прогрессируют с каждым дополнительным сверточным слоем. В представленном СНС в диагностическом процессе первого слоя могут быть использованы как фильтр основных признаков, например, максимальных или минимальных значений. То последующее выполнение операции свертки позволяет обнаружить признаки более высокого порядка, то есть расстояния между минимальными и максимальными значениями. Таким образом, структура сети будет зависеть от типа предоставляемой информации, а также от функции, выполняемой СНС.
Для обнаружения сложных объектов используются структуры, состоящие из нескольких наборов слоев. Способность обнаруживать признаки связана с процессом приобретения сетью навыков обобщения. В связи с обширной структурой СНС, методы, которые избегают чрезмерного соответствия, становятся очень важными.[6]
3. Математическая модель АД.
Входными данными для СНС являются фазные токи асинхронного двигателя. Для их получения используем модель, созданную в Matlab. Однако для моделирования несиметрии в АД стандартные блоки не подходят, так как в них происходит преобразование к вращающуюся системе координат dq, что приводит к потере важной информации для обучения нейросети.
Система дифференциальных уравнений (ДУ) электрического равновесия цепей статора и ротора асинхронного двигателя (АД) для мгновенных значений напряжений, токов и потокосцеплений, составленная с учетом допущений, в матричной форме имеет вид:
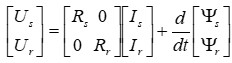
Рисунок 1 – Система дифференциальных уравнений электрического равновесия цепей статора и ротора асинхронного двигателя
где
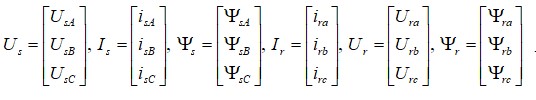
Векторы напряжений, токов и потокосцеплений фаз A, B, C статора и a, b, C ротора
Векторы напряжений, токов и потокосцеплений фаз A, B, C статора и a, b, c ротора
Rs=diag([RsA RsB RsC ]), Rr=diag([Rra Rrb Rrc ]) – диагональные матрицы активных сопротивлений соответственно фаз статора и ротора, приведенные к статору;
При условии полной симметрии АД (RsA=RsB=RsC=Rs, Rra =Rrb=Rrc=Rr) уравнение (Рис. 1) может быть разделено на два уравнения балансы напряжений отдельно статора и ротора, – тогда матрицы активных сопротивлений Rs и Rr могут быть заменены соответствующими скалярными величинами.
Уравнение движения ЭП на основе двигателя, ротор которого вращается, в котором не учтено возможное наличие упругих сил, имеет вид:
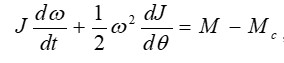
Рисунок 3 – Уравнение движения ЭП
где J – суммарный момент инерции ЭМС, приведенный к валу двигателя, который в общем случае является функцией углового положения ротора θ;
Mc – суммарный статический момент нагрузки, состоит из собственно момента нагрузки на валу двигателя и момента сухого трения и т.д.
В случаях, когда момент инерции не является функцией углового положения ротора, общее уравнение движения несколько упрощается и принимает вид:
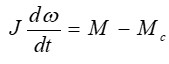
Рисунок 4 – Уравнение движения ЭП в случаях, когда момент инерции не является функцией углового положения ротора
Уравнения АД в фазных координатах описывают процессы в асинхронной машине, позволяя при этом не отходить от физической сути этих процессов. При помощи такой модели возможно также качественное исследование работы АД в условиях несимметрии АД или источника питания (штатная несимметрия или несимметричные режимы), при питании АД от неидеального источника питания (источник несинусоидального напряжения).
Однако такой модели характерен тот недостаток, что она содержит периодические коэффициенты в ДУ, что делает невозможным аналитическое их решение и значительно увеличивает длительность их численного решения
Для создания интерактивной математичемкой модели обратимся к пакету прикладных программ Matlab. Возможность многих блоков программы Simulink, кроме блока Integrator, обрабатывать векторные сигналы, позволяет создать очень компактную и наглядную модель АД в трехфазной системе координат. Этому же способствует наличие в составе Simulink блока Matlab Fcn библиотеки Functions&Tables, который создает интерфейс между Matlab-функциями и дополнением Simulink.
Структурная схема АД в фазных координатах, построенная на основании уравнений выше, изображена на Рисунке 5
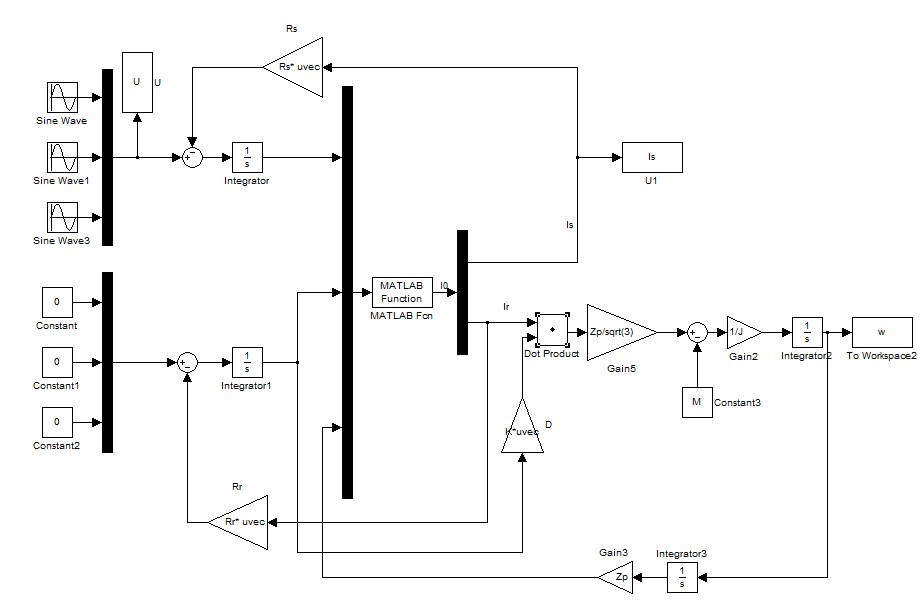
Рисунок 5 – Модель АДП
4. Результаты моделирования АД.
Исследуем асинхронный двигатель в нескольких состояниях. Изначально промоделируем АД в нормальном режиме, когда сопротивления обмоток статора равны. Результаты приведены на рисунке 6 и 7.
Рисунок 6 – Скорость и момент АД.
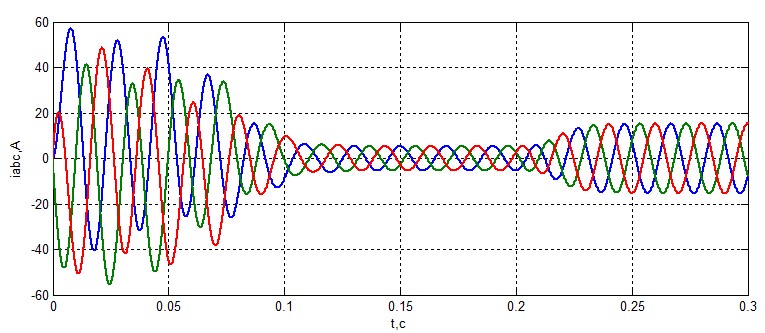
Рисунок 7 – Ток статора.
Из графиков видно, что модель работает и соответствует реальности. Из нее можно извлечь и графики тока ротора, но в этой работе они не пригодятся.
Следующим шагом станет моделирование несиметрии сопротивления обмоток статора. Изменим сопротивление обмотки фазы А на 1% (рис.8, 9) и 5% (рис.10, 11).
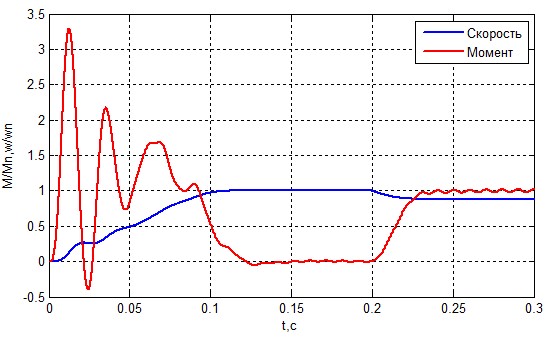
Рисунок 8 – Скорость и момент АД при ZsA=1.01 Zs.
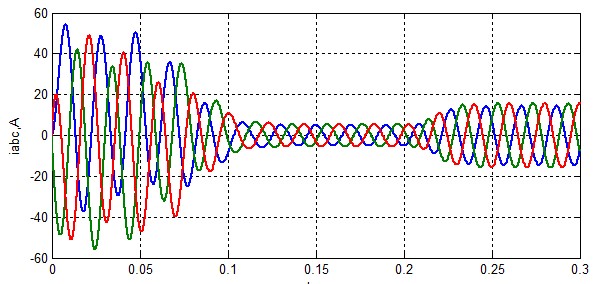
Рисунок 9 – Ток статора при ZsA=1.01 ZsA.
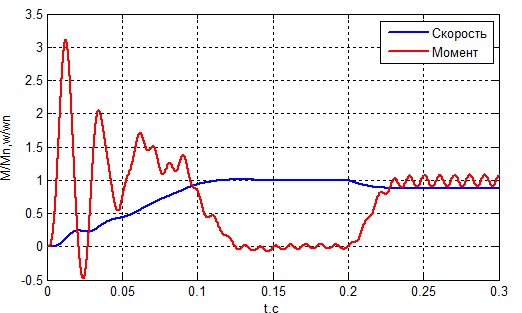
Рисунок 10 – Скорость и момент АД при ZsA=1.05 ZsA
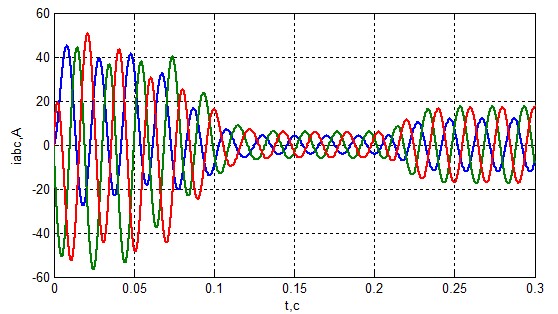
Рисунок 11 – Ток статора при ZsA=1.05 ZsA
Из графиков, приведенных выше следует, что несиметрия в статорной обмотке очень опасна для двигателя. При одном проценте отклонения разница не очевидна, но при пяти процентах четко прослеживается влияние несиметрии. Она приводит к перегрузке двигателя и уменьшению срока эксплуатации. Также это может привести к старению изоляции что в последствии приведет к иным аварийным ситуациям.
5. Сверточная нейронная сеть
Для классификации несиметрии в статорной обмотке в этой работе используется сверточная нейронная сеть. Входными данными для этой сети выступает ток статора, а выходными состояние двигателя.
Для создания нейронной сети я использую встроенную библиотеку Matlab Deep Network Designer. Она представляет из себя блочный редактор нейросетей. Здесь имеются все необходимые компоненты для сверточной нейронной сети.
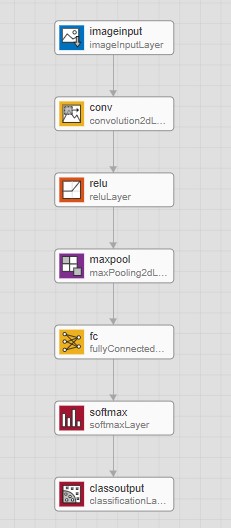
Рисунок 12 – Сверточная нейронная сеть в редакторе.
Разберем компоненты СНС:
- imageinput это блок входного слоя нейронной сети. В его параметрах задается количество входов. В данном случае матрица 50х40х3 (RGB матрица), то есть шесть тысяч входов.
- conv это непосредственно блок свертки. В его параметрах задается количество сверхточных фильтров, их размер и шаг по входной матрице.
- relu это функция ректификации, тоже что и функция активации, но по отношению к обычной сигмоиде увеличивает скорость обучения на порядок.
- maxpool это слой слой подвыборки. Функция этого слоя в сжатии полученных входных данных по определенному закону, в данном случае по максимальному значению. Это позволяет отбросить шум и пропустить полезный сигнал.
- fc это полносвязный слой. В этом слое каждый сигнал выходного слоя соединяется соединяется со всеми нейронами входного слоя. Каждая такая связь имеет свой вес, именно эти веса и будут настраиваться при обучении.
- softmax это блок который приобразует выходные слои так что их сумма всегда равна единице.
- classoutput это блок выполняет преобразования из вероятностного в классовый.
Перед тем как обучать нейронную сеть нужно подготовить входные данные. В нашем случае нам нужно преобразовать три тока статора в одну RGB матрицу размером 50х40х3.
Подход в данном случае прост. Снимаем по две тысячи точек тока каждой фазы. Графики сняты при номинальной скорости и моменте в установившемся режиме для упрощения обучения сети. Преобразуем каждый вектор тока в матрицу 50х40 и компонуем все три в один трёхмерный массив. Важно чтобы изменение тока были в пределах от 0 до 255 так как в RGB матрице данные типа uint32. Далее для наглядности преобразуем эти матрицы в изображения рис. 13 и 14
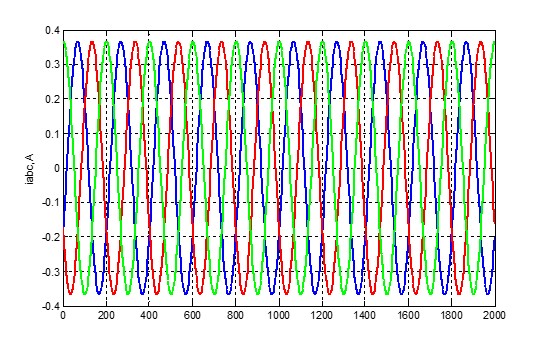
Рисунок 13 – Входные данные для нейросети до обработки.

Рисунок 14 – Входные данные для нейросети после обработки при различных значениях несиметрии.
(анимация 7 кадров, 7 циклов повторения, 6.12 килобайт)
Для обучения взят самый простой случай. Определение несиметрии в одной фазе. Чтобы обучить сеть необходимо использовать другую библиотеку под названием Transfer Learning Она позволяет просто и быстро обучить СНС.
Для обучения сняты графики здорового двигателя, и двигателя с несиметрией в фазе А. Один пакет данных для здорового двигателя, и 5 пакетов данных для поврежденного. Это сделано для ускорения обучения сети.
После того как сеть обучилась импортируем ее в среду Matlab, после чего ее можно использовать. Вызвать нейросеть можно двумя командами:
- Classify – эта команда выводит ответ в строковой форме.
- Predict – эта команда выводит ответ в матричной форме.
Проверим нашу СНС. Для этого подадим сначала пакет данных здорового двигатели. Затем пакет данных с несиметрией в фазе А.

Рисунок 15 – Демонстрация работы нейросети. а) здоровый двигатель; б) несиметрия в фазе А.
Как видно нейросеть справляется со своей задачей очень хорошо, даже при условии, что данных на обучение было мало. В дальнейшем я планирую увеличить количество классифицируемых неисправностей и заставить работать сеть онлайн.
Список источников
- Skowron M. Convolutional neural network-based stator current data-driven incipient stator fault diagnosis of inverter-fed induction motor / M. Skowron, T. Orlowska-Kowalska, M. Wolkiewicz, C. Kowalski // Energies 2020, 13(6) – p. 21.
- Chattopadhyay P. Deep learning in fault diagnosis of induction motor drives / P. Chattopadhyay, C. Delpha, N. Saha, J. Sil // Prognostics and system health management conference 2018 – p. 1064 – 1073.
- Jawadekar A. Arti?cial neural network-based induction motor fault classier using continuous wavelet transform / A. Jawadekar, S. Paraskar, S. Jadhav, G. Dhole // Systems science & control engineering: an open access journal 2014 – p. 684 – 690.
- Jigyasu R. Multiple Faults Diagnosis of Induction Motor Using Artificial Neural Network / R. Jigyasu, L. Mathew, A. Sharma \\ Springer Nature Singapore Pte Ltd. 2019 – p. 701 – 710.
- Lee J.H. Fault Diagnosis of Induction Motor Using Convolutional Neural Network / J.H. Lee, J.H. Pack, I.S. Lee \\ Appl. Sci. 2019, 9(15) – p.10.
- Gupta K. A Review on Fault Diagnosis of Induction Motor using Artificial Neural Networks / K. Gupta, A. Kaur \\ International Journal of Science and Research 2014 – p. 680 – 684.
- Lee K.M. Fault Diagnosis of Induction Motors Based on RBF Neural Network / K.M. Lee, P. Yarlagadda, Y.M. Lu\\ Applied Mechanics and Materials Vols. 462 – 463 2014 p. 85 – 88.
