Русский   English
ДонНТУ   Портал магістрів

Реферат по темі випускної роботи

Зміст

Введення

В даний час приводні системи на базі електродвигунів змінного струму відіграють ключову роль в промисловому застосуванні. Підраховано, що на ці машини припадає приблизно 29% світового і 69% промислового споживання електроенергії. При експлуатації електродвигунів в системах промислового приводу можуть виникати різного роду дефекти, що перешкоджають подальшій експлуатації машини. Згідно зі статистикою, найбільш поширеними дефектами електричних машин є пошкодження статора (37%), ротора (10%) і підшипника (41%). Проведені статичні випробування показують, що зі збільшенням номінальної потужності електродвигунів роль механічних пошкоджень на користь електричних зменшується. Цей факт обумовлює те, що багато наукових центрів зосереджені на розробці діагностичних методів, що дозволяють частково зменшити кількість електричних пошкоджень або виявити стан машини (зароджується Несправність), при якому вона ще може бути відремонтована.

Основою для роботи діагностичних систем є доскональне знання змін, що відбуваються в машині в результаті пошкодження. Спостереження за змінами, що відбуваються в машинах змінного струму, здійснюється за допомогою сигналів, доступних для вимірювання на досліджуваному об'єкті. Найбільш часто використовуються струми, напруги, вібрації, а також потік і температура. Ідея аналітичних методів оцінки технічного стану машини заснована на виділенні ознак пошкодження в вимірюваних діагностичних сигналах.

Використання аналітичного підходу в процесах виявлення несправностей електричних обмоток двигунів змінного струму пов'язано з необхідністю коригування параметрів вимірювання діагностичного сигналу на метод виділення ознак несправності. Використовувані в даний час аналітичні методи виявлення пошкоджень засновані на спостереженні змін сигналу в тимчасовій, частотній або чачтотно-тимчасової області. Серед них особливої уваги заслуговують наступні методи: швидке перетворення Фур'є(ШПФ), розширений векторний аналіз парку, короткочасне перетворення Фур'є, перетворення Гільберта-Хуана, А також вейвлет–аналіз у вигляді безперервного вейвлет-перетворення або дискретного вейвлет-перетворення. З представлених методів найбільш поширеним є використання аналізу ШПФ. Аналіз спектра сигналу забезпечує як ефективну оцінку симптомів пошкодження, так і не створює значного навантаження на обчислювальні системи. Однак, як і більшість аналітичних методів, ШПФ вимагає відносно тривалого часу вимірювання, що, особливо в разі між оборотних коротких замикань обмотки статора, є безсумнівним недоліком даного методу, обумовленим динамікою цих несправностей. Крім того, у багатьох випадках неможливо забезпечити стаціонарність сигналу протягом необхідного періоду вимірювання.

Розпізнавання змін діагностичних сигналів і їх оцінка в системах, заснованих на аналітичних методах, зазвичай виконуються людиною, що збільшує час виявлення несправностей. Більш того, такі системи часто не повністю автоматизовані, і кількість помилок часто пов'язано з досвідом людини-експерта.[3-4]

1. Актуальність теми

В даний час у зв'язку з динамічним розвитком методів штучного інтелекту діагностичні системи, засновані на аналітичних методах, поступово замінюються нейронними детекторами пошкоджень. Безсумнівною перевагою таких систем є обмежена роль людини-експерта в процесі оцінки технічного стану об'єкта, що забезпечує при цьому високу ефективність виявлення несправностей. Основою функціонування діагностичних систем на основі нейронних мереж (ОНМ), що застосовуються також для виявлення і класифікації несправностей асинхронних двигунів, є аналітичні методи. Тому вхідна інформація для таких систем є результатом вилучення симптомів з обраних діагностичних сигналів з використанням аналітичних методів.

Багатошарові нейронні мережі є найбільш популярними структурами, використовуваними в діагностичних методах, в тому числі в разі виявлення несправностей асинхронних і синхронних двигунів. Крім можливостей апроксимації даних, особливо важливим завданням діагностичних систем на основі нейромереж є класифікація пошкоджень. Основним представником класифікаторів, що використовуються в процесах виявлення несправностей, є самоорганізується мережа Кохонена. Перевагою деяких з них є його проста структура і той факт, що немає необхідності забезпечувати кілька навчальних вибірок.

Методи штучного інтелекту все частіше асоціюються з проблемою глибокого навчання. В основі структур глибокого навчання лежать класичні нейронні мережі. Однак глибокі нейронні мережі (ГНМ) характеризуються особливостями, відмінними від класичних неглибоких мереж, що є результатом відмови від універсального правила апроксимації. Використовувані досі структури, що мають максимум два прихованих шару, дозволили досягти задовільних результатів. Тим не менш, збільшення структури дозволило отримати ознаки нейромереж, які раніше були недосяжні в класичних неглибоких структурах.

Довгий час ГНМ використовувалися в основному в інформаційних системах (наприклад, обробка зображень, розпізнавання мови). За останній час спостерігається зростаючий інтерес до систем виявлення пошкоджень електричних машин на базі ГНМ. У більшості випадків вони пов'язані з аналізом механічних пошкоджень або механічних компонентів системи. Невелика кількість робіт, пов'язаних з електричними ушкодженнями Ім, в основному стосуються пошкоджень ротора. Більшість систем на основі ГНМ використовують вимірювання вібрації, рідше струмів статора і напруг. Цей факт випливає з явних змін, що відбуваються в діагностується сигналі, обумовлених механічним пошкодженням і випливає з цього простотою аналізу сигналу.[1-2]

2. Згорткові мережі

Серед використовуваних мережевих структур глибокого навчання найбільш часто використовуються згорткові нейронні мережі (ЗНМ). ЗНМ, використовувані в діагностичних додатках, характеризуються значно більш високим рівнем ефективності в порівнянні з іншими мережами. У діагностичних процесах ЗНМ може виступати в якості системи класифікації пошкоджень, а також надавати інформацію про ступінь пошкодження. Важливим аспектом при використанні ГНН в діагностичних процесах є відповідна настройка вимірюваного сигналу на структуру і властивості мережі. Вхідний вектор ГНМ може бути отриманий в результаті аналізу сигналу і безпосередньо наданого діагностичного сигналу. Завдяки принципу роботи структур глибокого навчання, в більшості випадків вимірюваний сигнал перетворюється в 2D або 3D матрицю.

В даній роботі представлена можливість використання ЗНМ в процесі виявлення несиметрії фаз. Розроблене додаток характеризується прямою обробкою необробленого діагностичного сигналу. Тут ознаки пошкодження витягуються безпосередньо з сигналів фазного струму статора, опускаючи добре відомі аналітичні методи попередньої обробки, такі як ШПФ, вейвлет і інші перетворення більш високого порядку.

Описана ідея діагностичної системи на базі ЗНМ, що виконує завдання виявлення несправностей і оцінки ступеня несиметрії обмоток статора АД. На відміну від методів, заснованих на простому аналізі вібраційного сигналу для виявлення механічних пошкоджень, розроблений метод полягає в прямій обробці сигналів фазного струму через ГНМ, що є одним з нових підходів в системах виявлення несправностей статора.

Слід підкреслити, що розробка діагностичної системи, заснованої на прямому аналізі струму статора, пов'язана з додатковими труднощами, пов'язаними з тим, несиметрія напруг і пошкодження обмотки викликає аналогічний ефект, як і збільшення моменту навантаження, тобто збільшення амплітуди струму статора. Однак діагностична система повинна виявляти характеристики пошкодження, тобто розрізняти вплив несиметрії і вплив умов роботи приводу на аналізований діагностичний сигнал. [5]

Основна функція ЗНМ полягає в добуванні ознак вищих порядків з аналізованого сигналу за допомогою згорткових операцій. Ці мережі не мають заздалегідь визначеної архітектури, методів вибору параметрів або правил, що стосуються кількості згорткових шарів.

Структуру ЗНМ слід розглядати як визначення ознак, які прогресують з кожним додатковим згортковим шаром. У представленому ЗНМ в діагностичному процесі першого шару можуть бути використані як фільтр основних ознак, наприклад, максимальних або мінімальних значень. Те подальше виконання операції згортки дозволяє виявити ознаки більш високого порядку, тобто відстані між мінімальними і максимальними значеннями. Таким чином, структура мережі буде залежати від типу наданої інформації, а також від функції, виконуваної ЗНМ.

Для виявлення складних об'єктів використовуються структури, що складаються з декількох наборів шарів. Здатність виявляти ознаки пов'язана з процесом придбання мережею навичок Узагальнення. У зв'язку з великою структурою ЗНМ, методи, які уникають надмірної відповідності, стають дуже важливими.[6]

3. Математична модель АД.

Вхідними даними для ЗНМ є фазні струми асинхронного двигуна. Для їх отримання використовуємо модель, створену в Matlab. Однак для моделювання несиметрії в АТ стандартні блоки не підходять, так як в них відбувається перетворення до обертову систему координат dq, що призводить до втрати важливої інформації для навчання нейромережі.

Система диференціальних рівнянь (ДР) електричної рівноваги ланцюгів статора і ротора асинхронного двигуна (АД) для миттєвих значень напруг, струмів і потокосцеплений, складена з урахуванням припущень, в матричній формі має вигляд:

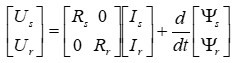
система диференціальних рівнянь електричного рівноваги ланцюгів статора і ротора асинхронного двигуна

Рисунок 1 – Система диференціальних рівнянь електричної рівноваги ланцюгів статора і ротора асинхронного двигуна

де

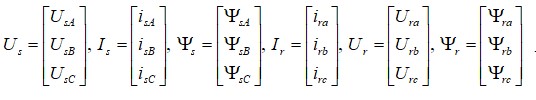
вектори напруг, струмів і потокосцеплений фаз A, B, C статора і a, b, C ротора;

Рисунок 2 – Вектори напруг, струмів і потокосцеплений фаз A, B, C статора і a, b, C ротора

Rs=diag ([RsA RsB RsC ]), Rr=diag ([Rra Rrb Rrc]) – діагональні матриці активних опорів відповідно фаз статора і ротора, наведені до статора;

За умови повної симетрії АТ (RsA=RsB=RsC=Rs, Rra =Rrb=Rrc=Rr) рівняння (Рис. 1) може бути розділене на два рівняння баланси напруг окремо статора і ротора, – тоді матриці активних опорів Rs і Rr можуть бути замінені відповідними скалярними величинами.

Рівняння руху ЕП на основі двигуна, ротор якого обертається, в якому не враховано можливу наявність пружних сил, має вигляд:

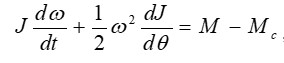
рівняння руху ЕП

Рисунок 3 – івняння руху ЕП

де J – сумарний момент інерції ЕМС, приведений до валу двигуна, який в загальному випадку є функцією кутового положення ротора θ.

Mc-сумарний статичний момент навантаження, складається з власне моменту навантаження на валу двигуна і моменту сухого тертя і т. д.

У випадках, коли момент інерції не є функцією кутового положення ротора, загальне рівняння руху дещо спрощується і набуває вигляду:

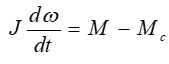
рівняння руху ЕП

Рисунок 4 – рівняння руху ЕП у випадках, коли момент інерції не є функцією кутового положення ротора

Рівняння АД у фазних координатах описують процеси в асинхронній машині, дозволяючи при цьому не відходити від фізичної суті цих процесів. За допомогою такої моделі можливо також якісне дослідження роботи АД в умовах несиметрії АД або Джерела живлення (штатна несиметрія або несиметричні режими), при харчуванні АД від неідеального Джерела живлення (джерело несинусоїдальної напруги).

Однак такій моделі характерний той недолік, що вона містить періодичні коефіцієнти в ДР, що унеможливлює аналітичне їх рішення і значно збільшує тривалість їх чисельного рішення

Для створення інтерактивної математичемкой моделі звернемося до пакету прикладних програм Matlab. Можливість багатьох блоків програми Simulink, крім блоку Integrator, обробляти векторні сигнали, дозволяє створити дуже компактну і наочну модель АД в трифазній системі координат. Цьому ж сприяє наявність у складі Simulink блоку Matlab Fcn бібліотеки Functions&Tables, який створює інтерфейс між Matlab-функціями і доповненням Simulink.

Структурна схема АТ в фазних координатах, побудована на підставі рівнянь вище, зображена на малюнку 5

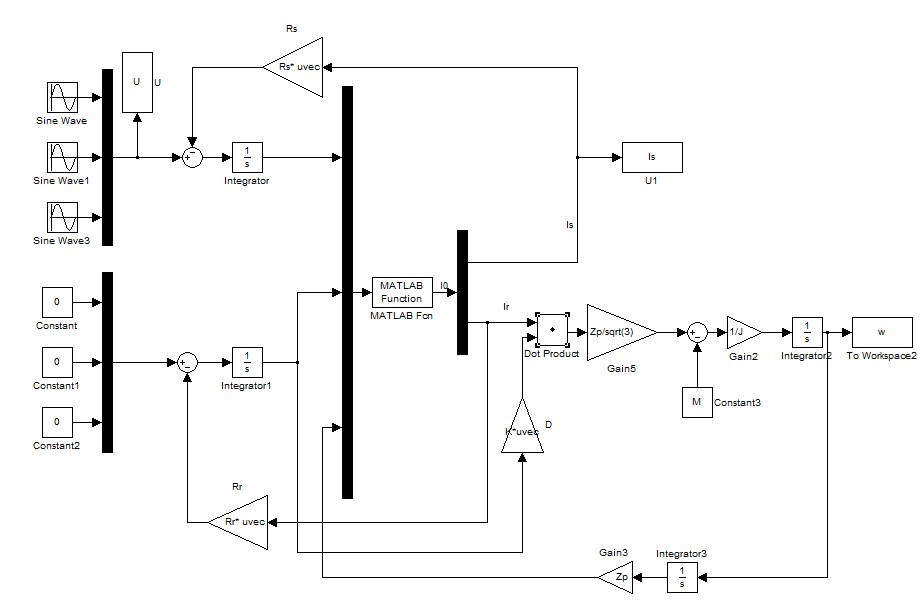
Рисунок 5 – Модель АД

Рисунок 5 – Модель АД

4. Результати моделювання АД.

Досліджуємо асинхронний двигун в декількох станах. Спочатку промоделюємо АТ в нормальному режимі, коли опору обмоток статора рівні. Результати наведені на малюнку 6 і 7

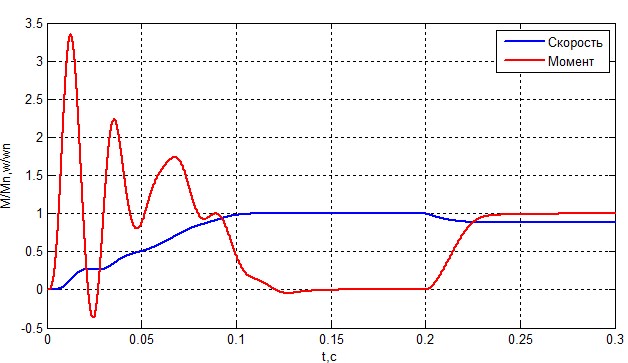
Малюнок 6-Швидкість і момент АД.

Рисунок 6 – Швидкість і момент АД.

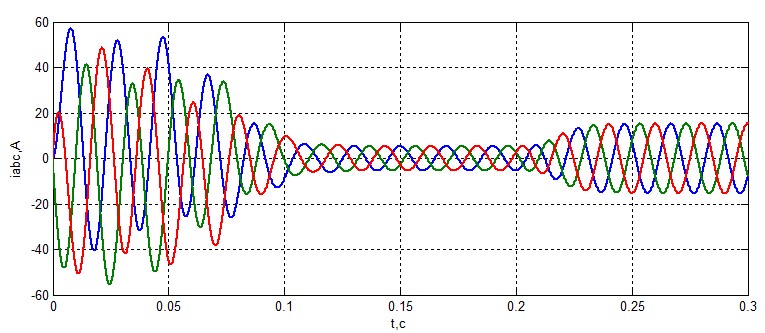
малюнок 7 – Струм статора.

Рисунок 7 – Струм статора.

З графіків видно, що модель працює і відповідає реальності. З неї можна витягти і графіки струму ротора, але в цій роботі вони не знадобляться.

Наступним кроком стане моделювання несиметрії опору обмоток статора. Змінимо опір обмотки фази а на 1% (рис.8, 9) і 5% (рис .10, 11).

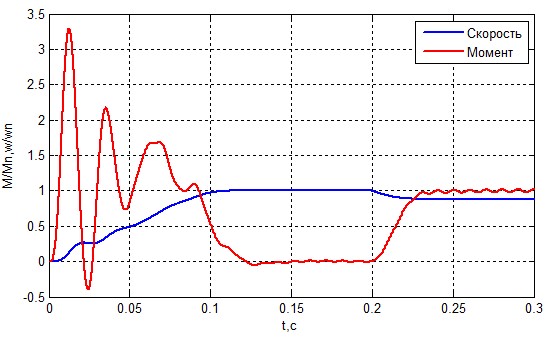
малюнок 8 – Швидкість і момент АД при ZsA=1.01 Zs.

Рисунок 8 – Швидкість і момент АТ при ZsA=1.01 Zs.

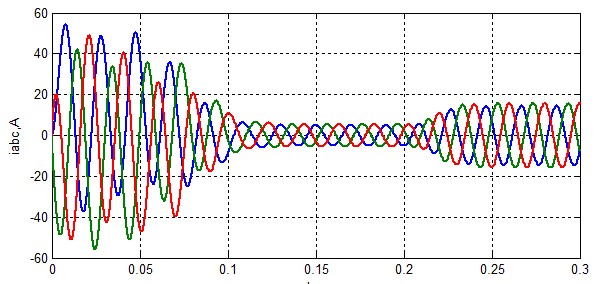
малюнок 9-струм статора при ZsA=1.01 ZsA.

Рисунок 9 – Струм статора при ZsA=1.01 ZsA.

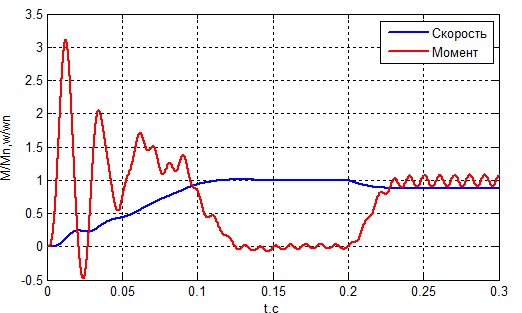
малюнок 10 – Швидкість і момент АД при ZsA=1.05 ZsA

Рисунок 10 – Швидкість і момент АТ при ZsA=1.05 ZsA < / p>

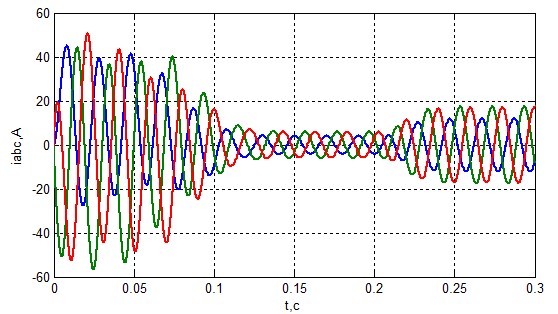
малюнок 11-струм статора при ZsA=1.05 ZsA

Рисунок 11 – Струм статора при ZsA=1.05 ZsA

З графіків, наведених вище слід, що несиметрія в статорної обмотці дуже небезпечна для двигуна. При одному відсотку відхилення різниця не очевидна, але при п'яти відсотках чітко простежується вплив несиметрії. Вона призводить до перевантаження двигуна і зменшення терміну експлуатації. Також це може привести до старіння ізоляції що надалі призведе до інших аварійних ситуацій.

5. Згорткова нейронна мережа

Для класифікації несиметрії в статорній обмотці в цій роботі використовується згорткова нейронна мережа. Вхідними даними для цієї мережі виступає струм статора, а вихідними стан двигуна.

Для створення нейронної мережі я використовую вбудовану бібліотеку Matlab Deep Network Designer. Вона представляє з себе блоковий редактор нейромереж. Тут є всі необхідні компоненти для згорткової нейронної мережі.

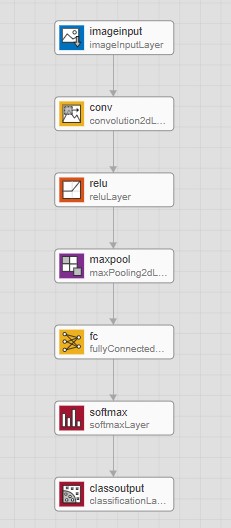
малюнок 12-Згорткова нейронна мережа в редакторі.

Рисунок 12 – Згорткова нейронна мережа в редакторі.

Розберемо компоненти ЗНМ:

Перед тим як навчати нейронну мережу потрібно підготувати вхідні дані. У нашому випадку нам потрібно перетворити три струму статора в одну rgb матрицю розміром 50х40х3.

Підхід в даному випадку простий. Знімаємо по дві тисячі точок струму кожної фази. Графіки зняті при номінальній швидкості і моменті в сталому режимі для спрощення навчання мережі. Перетворимо кожен вектор струму в матрицю 50х40 і компонуємо всі три в один тривимірний масив. Важливо щоб зміна струму були в межах від 0 до 255 так як в RGB матриці дані типу uint32. Далі для наочності перетворимо ці матриці в зображення рис. 13 і 14

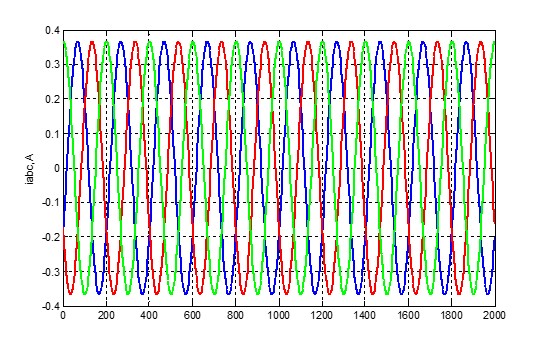
малюнок 13 - - вхідні дані для нейромережі до обробки.

Рисунок 13 – Згорткова нейронна мережа в редакторі.

малюнок 14 – – вхідні дані для нейромережі після обробки.

Рисунок 14 – Згорткова нейронна мережа в редакторі.


(анімація 7 кадрів, 7 циклів повторення, 6.12 кілобайт)

Для навчання взято найпростіший випадок. Визначення несиметрії в одній фазі. Щоб навчити мережу необхідно використовувати іншу бібліотеку під назвою Transfer Learning вона дозволяє просто і швидко навчити ЗНМ.

Для навчання зняті графіки здорового двигуна, і двигуна з несиметрією в фазі а. Один пакет даних для здорового двигуна, і 5 пакетів даних для пошкодженого. Це зроблено для прискорення навчання мережі.

Після того як мережа навчилася імпортуємо її в середу Matlab, після чого її можна використовувати. Викликати нейромережу можна двома командами:

Перевіримо нашу ЗНМ. Для цього подамо спочатку пакет даних. Потім пакет даних з несиметрією у фазі а.

малюнок 15 - - демонстрація роботи нейромережі. а) здоровий двигун; б) несиметрія у фазі а.

Рисунок 15 – Демонстрація роботи нейромережі. а) здоровий двигун; б) несиметрія в фазі а.

Як видно нейромережа справляється зі своїм завданням дуже добре, навіть за умови, що даних на навчання було мало. Надалі я планую збільшити кількість несправностей і змусити працювати мережу онлайн.

Список джерел

  1. Skowron M. Convolutional neural network-based stator current data-driven incipient stator fault diagnosis of inverter-fed induction motor / M. Skowron, T. Orlowska-Kowalska, M. Wolkiewicz, C. Kowalski // Energies 2020, 13(6) – p. 21.
  2. Chattopadhyay P. Deep learning in fault diagnosis of induction motor drives / P. Chattopadhyay, C. Delpha, N. Saha, J. Sil // Prognostics and system health management conference 2018 – p. 1064 – 1073.
  3. Jawadekar A. Arti?cial neural network-based induction motor fault classier using continuous wavelet transform / A. Jawadekar, S. Paraskar, S. Jadhav, G. Dhole // Systems science & control engineering: an open access journal 2014 – p. 684 – 690.
  4. Jigyasu R. Multiple Faults Diagnosis of Induction Motor Using Artificial Neural Network / R. Jigyasu, L. Mathew, A. Sharma \\ Springer Nature Singapore Pte Ltd. 2019 – p. 701 – 710.
  5. Lee J.H. Fault Diagnosis of Induction Motor Using Convolutional Neural Network / J.H. Lee, J.H. Pack, I.S. Lee \\ Appl. Sci. 2019, 9(15) – p.10.
  6. Gupta K. A Review on Fault Diagnosis of Induction Motor using Artificial Neural Networks / K. Gupta, A. Kaur \\ International Journal of Science and Research 2014 – p. 680 – 684.
  7. Lee K.M. Fault Diagnosis of Induction Motors Based on RBF Neural Network / K.M. Lee, P. Yarlagadda, Y.M. Lu\\ Applied Mechanics and Materials Vols. 462 – 463 2014 p. 85 – 88.