Content
- Introduction
- Relevance of the topic
- Purpose and objectives of the study, planned results
- Fractal model of solid phase formation
- Mathematical models of the growth of the solid phase of metal
- BML-model of solid growth of metal
- Conclusions
- List of sources
Introduction
The development of science and technology in the field of metallurgy requires new metallic materials with special physical, mechanical and chemical properties. To create them, it is necessary to study the physical nature of phase transitions during the formation of crystalline systems.
Of great importance is the development of the theory of phase transitions and the corresponding physical effects in concentrated crystalline phases formed from various initial media. Crystallization processes occupy a special place in the science of phase transitions. An important feature is the difference in crystallization kinetics between metals and alloys on the one hand and non-metals on the other. For example, during crystallization In multicomponent metal melts, the morphology of the interface of two contacting phases of the melt-crystal system plays a significant role. The morphology of the interface of contacting physical phases depends significantly on the temperature of the crystallizing systems. Upon reaching at a certain critical temperature, it becomes substantially rough on an atomic scale.
Relevance of the topic
At present, the problem of studying the morphology of the growing surface of the melt-crystal phase interface is urgent. Such a surface (crystallization front) is the boundary of the melt-crystal phase transition and moves along the alloy as it crystallizes. Known model J. Kahn, in which the structure of the interface does not contain elements of interaction between the particles of this surface. In [1], the inapplicability of this model to the crystallization of metallic melts was shown, which was confirmed by data on the kinetics of crystal growth in a number of experiments. Taking into account the peculiarities of the interaction of atoms or molecules at the interface of the contacting phases associated with the morphology of the interface, in the case of crystallization of multicomponent melts leads to kinetic effects associated with the disordering of the resulting crystalline phase, i.e. leads to the realization of processes order-disorder. The works indicate the presence of fluctuations in the values of the concentrations of solid state particles. Analysis of such fluctuations and accompanying physical processes is relevant.
An analysis of the existing mechanisms of crystal growth showed that they do not fully explain the experimental data, for example, the high crystallization rate of melts. The real crystallization rates of metals are several orders of magnitude higher than the maximum possible growth rate of the solid phase, calculated based on the generally accepted mechanism of sequential addition of new atoms to crystals from the liquid phase. Such values of the crystallization rate can be achieved only with the simultaneous attachment of a large number of particles or the attachment of aggregates of particles (clusters) with a structure close to the crystalline state to the solid phase.
The crystallization process takes place in conditions far from equilibrium. In front of the crystallization front, there is a boundary layer consisting of clusters. According to I. Prigogine [2], the properties of this layer differ significantly from the properties of a liquid and a solid phase. This allows us to consider it as an independent system. Within the framework of the concept of such a transitional boundary layer as an open system that exchanges energy with the environment, the processes occurring in it should be determined by the principle of minimum entropy production. Therefore, clusters are structures with a lower level of symmetry compared to the liquid phase. They arise in the boundary layer as a result of self-organization. Under conditions far from thermodynamic equilibrium, the structure of matter can be described using the mathematical apparatus of fractal geometry.
Purpose and objectives of the study, planned results
The object of research is the phase transition during crystallization of the metal from the melt. The subject of research is the growth models of the solid phase of the metal. Purpose: development of physical concepts of the kinetics of phase transition during the crystallization of metal from the melt and the formation of the primary crystal structure.
The main objectives of the research:
- to analyze the modern theory of crystallization of metals;
- analyze the growth models of the solid phase of the metal;
- describe the BML model modeling the growth of the solid phase of the metal;
- programmatically implement the BML-model of metal solid phase growth;
- carry out a fractal analysis of the simulation results.
The work is planned to obtain the following results:
- to show the relevance of modeling the growth of the solid phase of a metal for the development of physical concepts of the formation of the primary crystal structure;
- show the features of metal solid phase growth models;
- develop a BML model for the growth of a solid phase of a metal;
- to obtain fractal characteristics of the growth of the solid phase of a metal using the developed model.
Practical application of the obtained results is possible when carrying out computer engineering analysis in the field of computational materials science [3].
Fractal model of solid phase formation
In recent decades, it has been found that the structure of a substance formed under conditions far from thermodynamic equilibrium can be described using the mathematical apparatus of fractal geometry. Consequently, the structure of the substance constituting the critical nucleus is a fractal cluster. The works [4,5] provide the following confirmation of this statement:
- One of the main properties of fractal structures is the ability to capture a large space when using a small amount of substance. This becomes possible by creating an openwork, highly branched structure. This behavior of fractals during space capture makes it clear why the energy barrier is overcome in crystallizing systems during the formation of a nucleus of critical size rk.
- In order for the particles of the new phase to participate in chaotic thermal motion, their sedimentation stability is necessary, i.e. low rate of settling of particles to the bottom of the vessel. Fractal clusters have a much higher sedimentation stability compared to dense three-dimensional clusters due to their loose structure and, therefore, lower density.
- Another argument in favor of the fractal structure of the nuclei of a new phase is the smaller number of particles required for its formation in comparison with a dense cluster.
- The fractal structure of a critical nucleus is more realistic from the point of view of the statistical probability of collision of a small number of particles of the liquid phase (melt).
- The most significant factor due to which the crystallizing system has a fractal structure of nuclei of a new phase is the fact that the density of particles of a fractal cluster decreases from the center to the periphery. Therefore, for him, in fact, there is no interface with the environment. Its structure flows smoothly into the structure of the environment. Therefore, in the case of a fractal structure of a critical nucleus of a new phase, there is no energy barrier for its formation.
Thus, the appearance of solid phase nuclei in the form of fractal clusters is thermodynamically the most favorable process and can occur spontaneously.
At the stage of completion of the growth of primary fractal clusters in the system, competition arises between the processes of further growth of clusters by the cluster-particle mechanism (DLA mechanism) and the cluster-cluster aggregate mechanism (CCA-mechanism). The time interval with the presence of competing DLA / CCA mechanisms of aggregation of particles of the new condensed phase corresponds to a structural phase transition of the second order, at which further densification of the system occurs. This transition is shown in Fig. 1, where are indicated: 1 - area of competition between CCA and DLA-clustering processes; 2 - area of competition between the formation of fragments of grains and granular structure; 3 - zone of effects of structural post-crystallization.
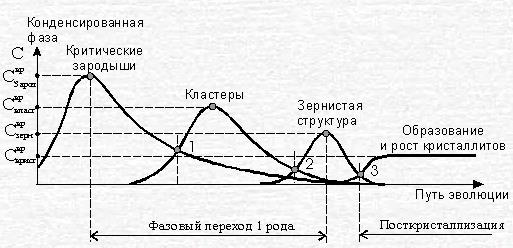
A phase transition of the second kind leads to the emergence in a nonequilibrium crystallizing system of the next scale level of hierarchical self-organization of the structure. Each large-scale level of organization of the hierarchical structure has its own "elementary elements", which are the final structures of the previous level. Since the process of compaction of a substance occurs during crystallization, these elementary elements are compaction elements. This means that at the initial stage of creating a large-scale level, the system builds a structure from the elements of the seal that is denser than the structure of the previous level. In contrast to the scale level of the construction of critical nuclei and primary fractal clusters, where individual atoms of the melt were the compaction elements, fractal clusters are the compaction elements at the next scale level of crystallization of the system.
Mathematical models of the growth of the solid phase of a metal
It is practically impossible to take into account all the factors leading to the spontaneous emergence of an ordered crystal structure from a disordered, chaotic environment. Therefore, it becomes necessary to abstract from the nature of the interaction of the building elements that make up the crystal. This abstraction leads to the emergence of purely mathematical models of growth processes. Such models can help identify and investigate the most common patterns of crystal growth.
Examples of deterministic parallel growth models have appeared in the literature on cellular automata, mathematical morphology, L-systems, and fractals. Cellular automata [6] are described by the state of the cell and transition functions. The transition function determines the new state of a cell based on its current state and, possibly, the state of neighboring cells. In general, this can lead to a finite or infinite, periodic or chaotic growth process. The study of such processes [7] has shown the possibility of the appearance of rather complex and interesting growth structures. A well-known example of growth on cellular automata is the game "Life" [8]. In mathematical morphology [9], structural elements are used to perform expansion and destruction of a shape or structure. In L-systems and fractals [10,11], individual cells are recursively replaced by the cell structure. Such processes produce self-similar scale-invariant structures.
BML-model of metal solid phase growth
In the master's thesis, the BML (Biham-Middleton-Levine) model is proposed for modeling the crystallization of metal. It is known as a self-organizing traffic flow model based on a deterministic cellular automaton. Moving elements are represented by dots on the grid with a random starting position. The BML model is a two-dimensional analogy of motion according to rule 184. As shown in Fig. 1, three states can be distinguished during the melt-crystal phase transition: initial structure with critical nuclei, cluster structure, granular structure.
The BML model of metal crystallization implemented in the R environment has two functions. The grid = createBMLGrid (r = 50, c = 50, density = 0.5) function creates a working field of the cellular automaton with the dimensions of cells. The density parameter is the density of the placement of solid elements on the working field (p). The g = runBMLGrid (grid, numSteps = 1024, ifPlot = TRUE, method = "slow") function performs the modeling process on the grid workspace with numSteps / 2 iterations. If the parameter ifPlot = TRUE, then the working field of the cellular automaton will be shown on the screen. The variable method can take one of two values: "slow" (mode with plotting the crystallization process) and "fast" (mode without plotting a plot). The model allows, depending on the value of the density parameter, to obtain structures: with critical nuclei, cluster, granular.
Conclusions
- BML-model of the growth of a solid part of the metal has been developed.
- The software implementation of the model is performed in the R. programming environment.
- When the program is running, depending on the density parameter, the following results are obtained: in the density range from 0.1 to 0.3, the metal has a structure with critical nuclei, in the density range from 0.4 to 0.6, the metal has a cluster structure , in the range of density change from 0.7 to 0.9, the metal has a granular structure.
Practical application of the results obtained is possible when conducting computer engineering analysis in the field of computational materials science.
LIST OF SOURCES
- Гуров К.П., Смирнов Е.А., Шабалин А.Н. Диффузия и кинетика фазовых превращений в металлах и сплавах. М.: МИФИ, 1990. – 80 с.
- Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур. М.: Мир, 2002. – 461 с.
- Огородникова О.М. Консолидированный компьютерный анализ процессов получения и эксплуатации металлических материалов в машиностроении. Диссертация на соискание ученой степени доктора технических наук. Екатеринбург – 2015. – 332 с.
- Смирнов Б.М. Физика фрактальных кластеров. М.:Наука, 1991.– 134 с.
- Стенли Х. Фракталы в физике. М.: Мир, 1988. – 463 с.
- Wolfram S. Theory and Applications of Cellular Automata. World Scientific, Singapore, 1986.
- Schrandt R.G., Ulam S. On recursively defined geometrical objects and patterns of growth. University of California Press, Berkeley, CA, 1990.
- Conway J. Winning Ways for Mathematical Plays. Academic Press, London, 1985.
- Serra J. Image Analysis and Mathematical Morphology. Academic Press, London, 1982.
- Prusinkiewicz P., Hanan J., Lindenmayer A. Systems, Fractals, and Plants. Springer-Verlag, New York, 1989.
- Prusinkiewicz P., Lindenmayer A. The Algorithmic Beauty of Plants. Springer-Verlag, New York, 1990.
