Реферат за темою випускної роботи
Зміст
- Введення
- Актуальність теми
- Мета і завдання дослідження, плановані результати
- Фрактальна модель освіти твердої фази речовини
- Математичні моделі зростання твердої фази металу
- BML-модель зростання твердої фази металу
- Висновки
- Список джерел
Введення
Розвиток науки і техніки в галузі металургії вимагає нових металевих матеріалів з особливими фізичними, механічними і хімічними властивостями. Для їх створення необхідно вивчення фізичної природи фазових переходів при утворенні кристалічних систем.
Велике значення має розвиток теорії фазових переходів і відповідних їм фізичних ефектів в концентрованих кристалічних фазах, що формуються з різних вихідних середовищ. Особливе місце в науці про фазових переходах займають процеси кристалізації. важливою особливістю є відмінність в кінетиці кристалізації між металами і сплавами з одного боку і неметалами з іншого. Наприклад, при кристалізації багатокомпонентних металевих розплавів істотну роль грає морфологія поверхні розділу двох дотичних фаз системи розплав-кристал. Морфологія поверхні розділу дотичних фізичних фаз істотно залежить від температури кристалізується систем. при досягненні поверхнею розділу фаз деякої критичної температури вона стає істотно шорсткою в атомному масштабі.
Актуальність теми
В даний час актуальною є задача вивчення морфології зростаючої поверхні розділу фаз розплав-кристал. Така поверхня (фронт кристалізації) є кордоном фазового переходу розплав - кристал і переміщається по металу в міру його кристалізації. Відома модель Дж. Кана, в якій структура поверхні розділу фаз не містить елементів взаємодії між частинками цієї поверхні. В роботі [1] була показана непридатність цієї моделі до випадків кристалізації металевих розплавів, що підтвердилося даними з кінетики росту кристалів в ряді експериментів. Врахування особливостей взаємодії атомів або молекул на межі поділу дотичних фаз, пов'язаних з морфологією поверхні розділу, в разі кристалізації багатокомпонентних розплавів призводить до кінетичним ефектів, пов'язаних з процесами разупорядочения утворюється кристалічної фази, тобто призводить до реалізації процесів порядок-безлад. У роботах зазначено про наявність флуктуацій величин концентрацій частинок твердого стану. Актуальним є аналіз таких флуктуацій і супутніх їм фізичних процесів.
Аналіз існуючих механізмів росту кристалів показав, що вони в повній мірі не пояснюють експериментальні дані, наприклад, високу швидкість кристалізації розплавів. Реальні швидкості кристалізації металів на кілька порядків перевищують максимально можливу швидкість росту твердої фази, розраховану виходячи з загальноприйнятого механізму послідовного приєднання нових атомів до кристалів з рідкої фази. Такі значення швидкості кристалізації можна досягти лише при одночасному приєднання великого числа частинок або приєднання до твердої фазі агрегатів частинок (кластерів) з близьким до кристалічному станом будовою.
Процес кристалізації протікає в далеких від рівноваги умовах. Перед фронтом кристалізації існує прикордонний шар, що складається з кластерів. За даними І. Пригожина [2] властивості цього шару значно відрізняються від властивостей рідини і твердої фази. Це дозволяє розглядати його в якості самостійної системи. В рамках уявлень про такий перехідному прикордонному шарі як відкритої, обмінюється енергією з навколишнім середовищем системі, що відбуваються в ньому процеси, повинні визначатися принципом мінімального виробництва ентропії. Тому кластери є структурами з більш низьким у порівнянні з рідкою фазою рівнем симетрії. Вони виникають в прикордонному шарі як результат самоорганізації. В умовах, далеких від термодинамічної рівноваги, структура речовини може бути описана за допомогою математичного апарату фрактальної геометрії.
Мета та завдання дослідження, плановані результати
Об'єктом дослідження є фазовий перехід при кристалізації металу з розплаву. Предмет дослідження - моделі зростання твердої фази металу. Мета: розвиток фізичних уявлень про кінетику фазового переходу при кристалізації металу з розплаву і формуванні первинної кристалічної структури.
Основні завдання дослідження:
- провести аналіз сучасної теорії кристалізації металів;
- провести аналіз моделей зростання твердої фази металу;
- описати BML-модель моделювання росту твердої фази металу;
- програмно реалізувати BML-модель зростання твердої фази металу;
- провести фрактальний аналіз результатів моделювання.
В роботі планується отримати наступні результати:
- показати актуальність моделювання росту твердої фази металу для розвитку фізичних уявлень про формування первинної кристалічної структури;
- показати особливості моделей зростання твердої фази металу;
- розробити BML-модель зростання твердої фази металу;
- отримати фрактальні характеристики росту твердої фази металу з використанням розробленої моделі.
Практичне застосування отриманих результатів можливо при проведенні комп'ютерного інженерного аналізу в області обчислювального матеріалознавства [3].
Фрактальна модель освіти твердої фази речовини
В останні десятиліття було встановлено, що структура речовини, що утворюється в умовах, далеких від термодинамічної рівноваги, може бути описана за допомогою математичного апарату фрактальної геометрії. Отже, структура речовини, що становить критичний зародок є фрактальним кластером. У роботах [4,5] наведені такі підтвердження цьому твердженню:
- Одне з основних властивостей фрактальних структур - здатність захоплювати великий простір при використанні малої кількості речовини. Це стає можливим за рахунок створення ажурною, сильно розгалуженої структури. Така поведінка фракталів при захопленні простору робить зрозумілим той факт, чому в кристалізуються системах відбувається подолання енергетичного бар'єру при утворенні зародка критичного розміру rk.
- Для того, щоб частинки нової фази могли брати участь в хаотичному тепловому русі, необхідна їх седиментаційна стійкість, тобто низька швидкість осідання частинок на дно посудини. Фрактальні кластери мають значно більшу седиментаційною стійкістю в порівнянні з щільними тривимірними кластерами в силу своєї пухкої структури і, отже, меншої щільності.
- Ще одним аргументом, що говорить на користь фрактального будови зародків нової фази, є менша в порівнянні з щільним кластером кількість частинок, необхідне для його освіти.
- Фрактальна структура критичного зародка більш реалістична з точки зору статистичної ймовірності зіткнення невеликого числа частинок рідкої фази (розплаву).
- Найбільш істотним фактором, завдяки якому кристалізується система має фрактальну структуру зародків нової фази, є той факт, що щільність частинок фрактального кластера знижується від центру до периферії. Тому для нього, фактично, не існує поверхні розділу з навколишнім середовищем. Його структура плавно перетікає в структуру навколишнього середовища. Тому в разі фрактального будови критичного зародка нової фази не існує енергетичного бар'єру для його освіти.
Таким чином, поява зародків твердої фази в вигляді фрактальних кластерів виявляється термодинамічно найбільш вигідним процесом і може відбуватися мимовільно.
На етапі завершення росту первинних фрактальних кластерів в системі виникає конкуренція між процесами подальшого зростання кластерів за механізмом кластер-частка (DLA-механізм) і механізму кластер-кластерний агрегат (CCA-механізм). Часовий інтервал з наявністю конкуруючих DLA / CCA-механізмів агрегації часток нової конденсованої фази відповідає структурному фазового переходу другого роду, при якому відбувається подальше ущільнення системи. Такий перехід показаний на рис. 1, де позначені: 1 - ділянка конкуренції CCA і DLA-процесів кластеризації; 2 - ділянка конкуренції формування фрагментів зерен і зернистої структури; 3 - зона ефектів структурної посткрісталлізаціі.
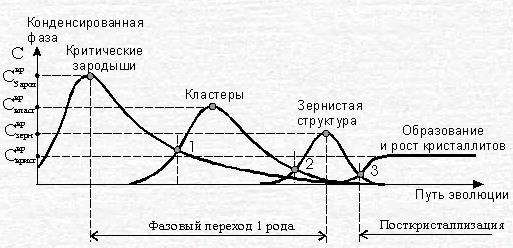
Фазовий перехід другого роду призводить до виникнення в нерівноважної кристалізується системі наступного масштабного рівня ієрархічної самоорганізації структури. Кожен масштабний рівень організації ієрархічної структури має свої «елементарні елементи», які є кінцевими структурами попереднього рівня. Оскільки при кристалізації відбувається процес ущільнення речовини, ці елементарні елементи є елементами ущільнення. Це означає, що на початковому етапі створення будь-якого масштабного рівня система робить з елементів ущільнення структуру, більш щільну в порівнянні зі структурою попереднього рівня. На відміну від масштабного рівня побудови критичних зародків і первинних фрактальних кластерів, на якому елементами ущільнення були окремі атоми розплаву, на наступному масштабному рівні кристалізації системи елементами ущільнення є фрактальні кластери.
Математичні моделі зростання твердої фази металу
Врахувати всі фактори, що призводять до мимовільного виникнення впорядкованої кристалічної структури з невпорядкованою, хаотичною середовища, практично не представляється можливим. Тому виникає необхідність абстрагуватися від природи взаємодії будівельних елементів, з яких складається кристал. Це абстрагування призводить до виникнення чисто математичних моделей ростових процесів. Такі моделі можуть допомогти виявити і досліджувати найбільш загальні закономірності кристалічного зростання.
Приклади моделей детермінованих моделей паралельного зростання з'явилися в літературі по клітинним автоматам, математичної морфології, L-системам і фракталам. Клітинні автомати [6] описуються станом осередки і функціями переходу. Функція переходу визначає новий стан осередку, виходячи з її поточного стану і, можливо, стану сусідніх осередків. У загальному випадку це може привести до кінцевого або нескінченного, періодичному або хаотичному процесу зростання. Дослідження таких процесів [7] показало можливість виникнення досить складних і цікавих структур зростання. Відомим прикладом зростання на клітинних автоматах є гра «Життя» [8]. У математичної морфології [9] використовуються структурні елементи для виконання розширення і руйнування форми або структури. В L-системах і фрактали [10,11] окремі осередки рекурсивно замінюються структурою осередків. Такі процеси справляють самоподібні масштабно-інваріантні структури.
BML-модель зростання твердої фази металу
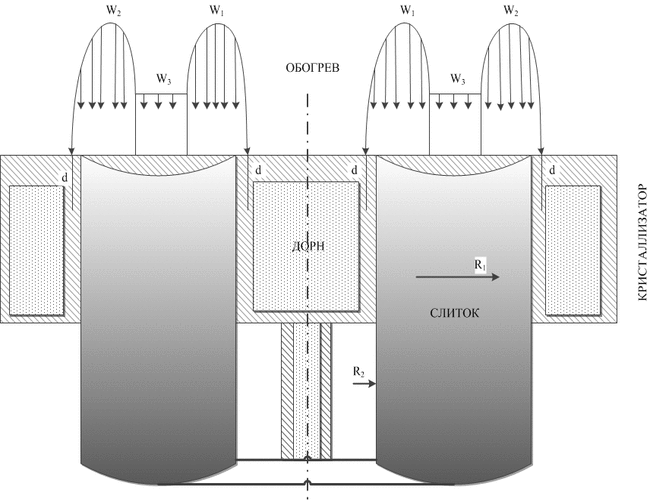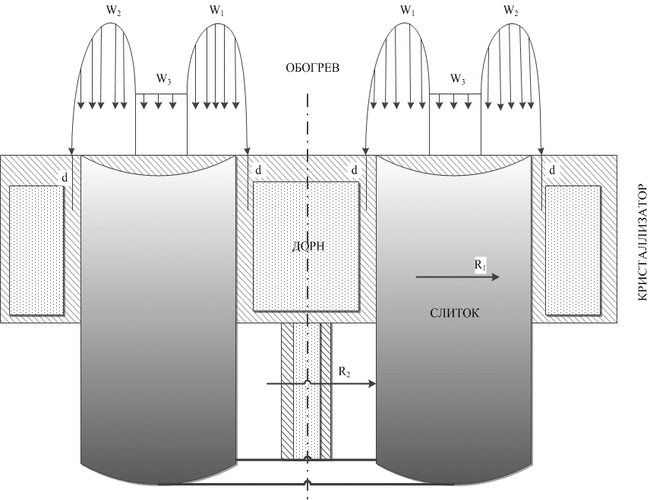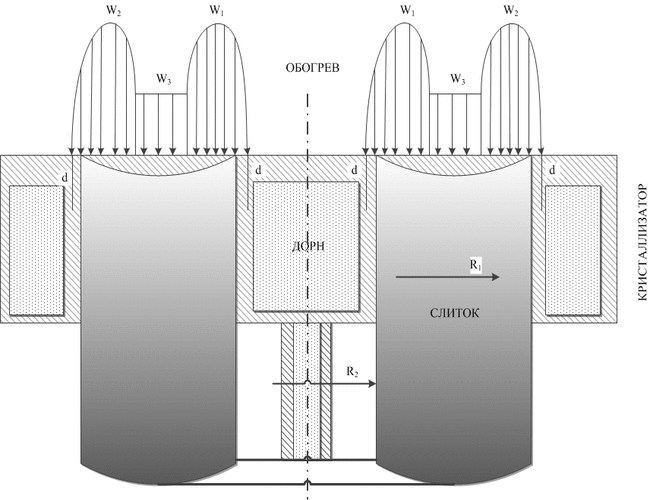
У магістерській дисертації для моделювання кристалізації металу пропонується модель BML (Biham-Middleton-Levine). Вона відома як самоорганізована модель транспортного потоку на основі детермінованого клітинного автомата. Рухливі елементи представлені точками на решітці з випадковим стартовим становищем. Модель BML є двовимірної аналогією руху за правилом 184. Як показано на малюнку 1, при фазовому переході розплав-кристал можна виділити три стану: початкова структура з критичними зародками, кластерна структура, зерниста структура.
Реалізована в середовищі R BML-модель кристалізації металу має дві функції. Функція grid = createBMLGrid (r = 50, c = 50, density = 0.5) створює робоче поле клітинного автомата розмірністю осередків. Параметр density - щільність розміщення на робочому полі твердих елементів (p). Функція g = runBMLGrid (grid, numSteps = 1024, ifPlot = TRUE, method = "slow") виконує процес моделювання на робочому полі grid з кількістю ітерацій numSteps / 2. Якщо параметр ifPlot = TRUE, то робоче поле клітинного автомата буде показано на екрані. Мінлива method може приймати одне з двох значень: "slow" (режим з побудовою графіка процесу кристалізації) і "fast" (режим без побудови графіка). Модель дозволяє в залежності від значення параметра density отримувати структури: з критичними зародками, кластерну, зернисту.
Висновки
- Розроблено BML-модель зростання твердої частини металу.
- Програмна реалізація моделі виконана в середовищі програмування R.
- При роботі програми в залежності від параметра density отримані наступні результати: на інтервалі зміни density від 0,1 до 0,3 метал має структуру з критичними зародками, на інтервалі зміни density від 0,4 до 0,6 метал має кластерну структуру , на інтервалі зміни density від 0,7 до 0,9 метал має зернисту структуру.
Практичне застосування отриманих результатів можливо при проведенні комп'ютерного інженерного аналізу в області обчислювального матеріалознавства.
Список джерел
- Гуров К.П., Смирнов Е.А., Шабалин А.Н. Диффузия и кинетика фазовых превращений в металлах и сплавах. М.: МИФИ, 1990. – 80 с.
- Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур. М.: Мир, 2002. – 461 с.
- Огородникова О.М. Консолидированный компьютерный анализ процессов получения и эксплуатации металлических материалов в машиностроении. Диссертация на соискание ученой степени доктора технических наук. Екатеринбург – 2015. – 332 с.
- Смирнов Б.М. Физика фрактальных кластеров. М.:Наука, 1991.– 134 с.
- Стенли Х. Фракталы в физике. М.: Мир, 1988. – 463 с.
- Wolfram S. Theory and Applications of Cellular Automata. World Scientific, Singapore, 1986.
- Schrandt R.G., Ulam S. On recursively defined geometrical objects and patterns of growth. University of California Press, Berkeley, CA, 1990.
- Conway J. Winning Ways for Mathematical Plays. Academic Press, London, 1985.
- Serra J. Image Analysis and Mathematical Morphology. Academic Press, London, 1982.
- Prusinkiewicz P., Hanan J., Lindenmayer A. Systems, Fractals, and Plants. Springer-Verlag, New York, 1989.
- Prusinkiewicz P., Lindenmayer A. The Algorithmic Beauty of Plants. Springer-Verlag, New York, 1990.
