Abstract
Content
- INTRODUCTION
- 1. BASIC CONCEPTS OF AUTOMATA THEORY
- 1.1 Planning of the States and their transitions
- 1.2 Implementation of a simple finite state machine
- 1.3 Using the state machine
- 1.4 Given the machines
- CONCLUSION
- REFERENCES
INTRODUCTION
The theory of automata as a scientific discipline arose within the framework of the theory of control systems (theoretical cybernetics) in the middle of the twentieth century, during the period of the rapid development of electronic computing technology and the corresponding areas of mathematical knowledge.
It took the development of a theoretical basis for solving problems that arose in the design of real digital computers, as well as in the process of building and researching hypothetical systems, such as neural networks. Finite automata were considered as models of the latter.
The development of information technology has brought the field of application of the theory of automata far beyond the modeling of digital electronics hardware, expanding it to the fundamental foundations of modern theoretical computer science.
Today, abstractions and models developed in the theory of automata are in demand in such scientific disciplines as the theory of formal grammars, mathematical linguistics, theory of logical models, mathematical logic and formal axiomatic systems, coding theory, theory of computational complexity, and others.
The theory of automata is most closely connected with the theory of algorithms and, in particular, with such a section of it as the theory of abstract machines.
Currently, there are a number of educational and educational–methodological publications, the titles of which contain the phrase "theory of automata".
Often these publications are of a synthetic nature, combining under one cover both elements of the theory of automata itself and fragments of the above scientific areas in which the apparatus of this theory finds powerful and fully justified application.
1. BASIC CONCEPTS OF THE THEORY OF AUTOMATORS
A finite state machine is some abstract model containing a finite number of states of something. It is used to represent and control the flow of execution of any commands. The state machine is ideal for implementing artificial intelligence in games, getting a neat solution without writing bulky and complex code [1].
A finite state machine (or simply FSM – Finite–state machine) is a computation model based on a hypothetical state machine. Only one state can be active at a time. Therefore, in order to perform any action, the machine must change its state.
State machines are commonly used to organize and represent the flow of execution of something. This is especially useful when implementing AI in games. For example, to write the "brain" of the enemy: each state represents some kind of action (attack, dodge, etc.).
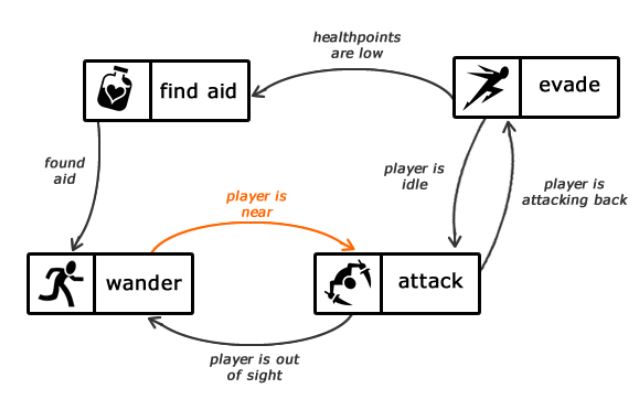
Figure 1.1 — Description of the states of the machine
A finite state machine can be represented as a graph, the vertices of which are states, and the edges are transitions between them. Each edge has a label that informs when the transition should occur. For example, in the image above, you can see that the machine will change the state "wander" to the state "attack" provided that the player is nearby.
1.1 Planning states and their transitions
The implementation of a state machine begins by identifying its states and transitions between them. Imagine a state machine describing the actions of an ant carrying leaves into an anthill [2].
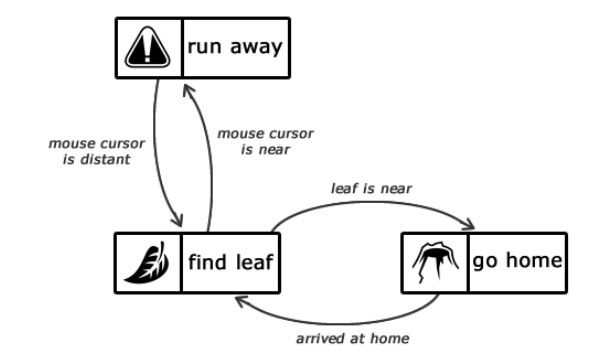
Figure 1.2 — Description of the states of intelligence of an ant
The starting point is the "find leaf" state, which remains active until the ant finds a leaf. When this happens, the state will change to "go home". The same state will remain active until our ant gets to the anthill. After that, the state changes back to "find leaf".
If the "find leaf" state is active, but the mouse cursor is near the ant, then the state changes to "run away". Once the ant is at a safe enough distance from the mouse cursor, the state will change back to "find leaf".
It is necessary to pay attention to the fact that when heading home or from home, the ant will not be afraid of the mouse cursor. Why? But because there is no corresponding transition.
It is worth noting that there is no transition between "run away" and "go home".
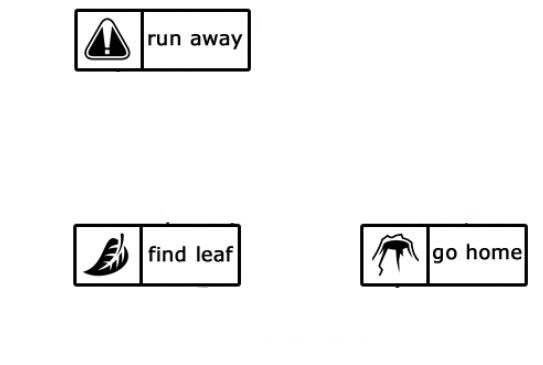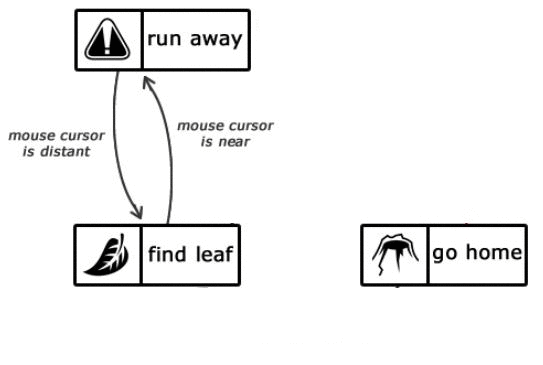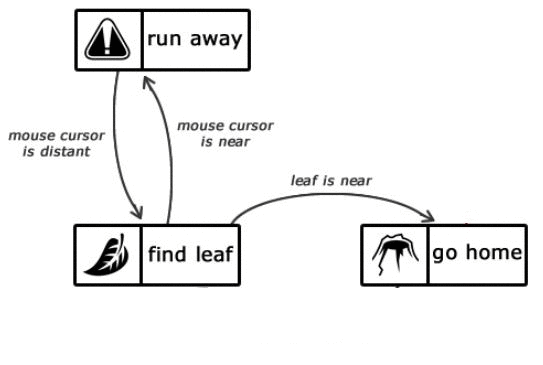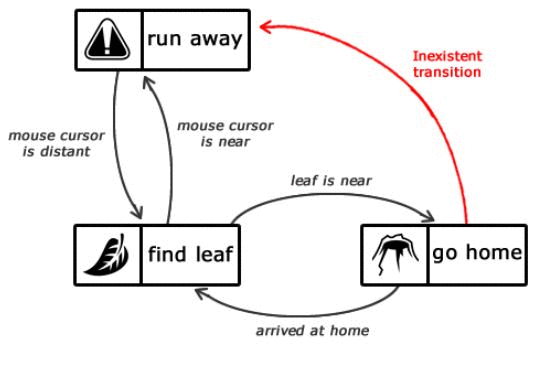
Figure 1.3 — Description of the states of intelligence of the ant
(animation: 6 frames, 6 repetition cycles, 100 kilobytes)
1.2 Implementation of a simple state machine
A state machine can be implemented with a single class. Let's call it FSM.
The idea is to implement each state as a method or function.
We will also use the activeState property to determine the active state.

Figure 1.4 — Implementation of the state machine
Every state is a function [3].
Moreover, such that it will be called every time the game frame is updated.
As mentioned, activeState will store a pointer to the active state function.
The update () method of the FSM class must be called every frame of the game.
And he, in turn, will call the function of the state that is currently active.
The setState () method will set the new active state.
Moreover, each function that defines some state of the automaton does not have to belong to the FSM class – this makes our class more universal.
1.3 Using a state machine
Implementing the AI ??of the ant. Above, we have already shown a set of its states and transitions between them. Let's illustrate them again, but this time we'll focus on the code.
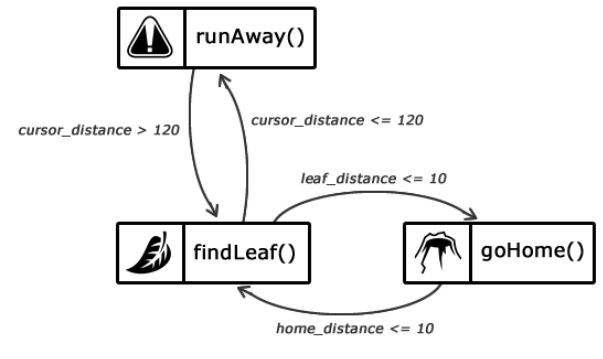
Figure 1.5 — Description of the states of intelligence of an ant
Our ant is represented by the Ant class, which has a brain field. This is just an instance of the FSM class.
The Ant class also contains velocity and position properties. These variables will be used to calculate the motion using Euler's method. The update () function is called every time the game frame is updated.
To understand the code, we will omit the implementation of the moveBasedOnVelocity () method. For more information on movement, read the Understanding Steering Behaviors series.
Below is the implementation of each of the methods, starting with findLeaf () – the state responsible for finding leaves [4].

Figure 1.6 — Description of the state responsible for finding leaves

Figure 1.7 — The state of goHome ()
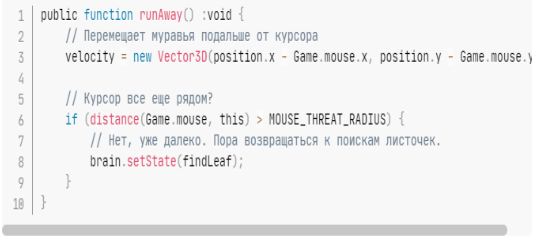
Figure 1.8 — State runAway ()
Finite state machines are certainly useful for implementing artificial intelligence logic in games.
They can be easily represented as a graph, allowing the developer to see all the possible options.
Implementing a state machine with stateful functions is a simple yet powerful technique.
Even more complex interweaving of states can be implemented with FSM.
1.4 Given machines
An automaton is called reduced if it does not contain unattainable states and none of its two states are equivalent to each other.
If the automaton is unreduced, then one can obtain an automaton equivalent to it with a smaller number of states either by discarding unattainable states, or by combining two equivalent states into one, as shown in the two previous sections.
The reduction process can be repeated until the reduced automaton is obtained. Thus, for each finite automaton there is an equivalent reduced automaton.
The reduced automaton obtained in this way has fewer states than the original one (if the original one was not already reduced), and can be more compactly implemented on a computer.
The reduced automaton obtained in this way has fewer states than the original one (if the original one was not already reduced), and can be more compactly implemented on a computer.
However, these automata will be virtually the same in all respects, except for the names by which their states are named.
CONCLUSION
Within the framework of this work, a number of experiments with automata were carried out, which allow formulating a procedure for generating one automaton from another. This procedure consists in constructing Pk–tables for the automaton A'UB and redefining the arcs to be thrown in A 'in such a way that during the transfer, each class of each Pk–table consisted of the same number of states of the automaton A' and the automaton B.
This procedure has the property of non–determinism and will subsequently be presented in the form of an algorithm.
References
- Брауэр, В. Введение в теорию конечных автоматов / [пер. с нем]. – М.: Радио и связь, 1987. – 392 с.
- Гуренко, В. В. Введение в теорию автоматов / В. В. Гуренко – Москва: МГТУ им. Н. Э. Баумана, 2013. – С. 4–19.
- Капитонова, Ю. В. Основы дискретной математики / Ю. В. Капитонова, С. Л. Кривий, А. А. Летичевский, Г. М. Луцкий, Н. К. Печурин. – К.: Наукова думка, 2002. – 568 с.
- Ковалев Д. В., Копытова О. М. Разработка и исследование метода построения функции деградации поведения конечного автомата в результате переброски дуг // Сборник материалов II Международной научно–практической конференции
Программная инженерия: методы и технологии разработки информационно–вычислительных систем
(ПИИВС–2018). – Донецк: ДонНТУ, 2018. – С. 230 – 233. - Буевич, В. А. Автомат конечный / В. А. Буевич [Электронный ресурс]. – Режим доступа: https://scanwordbase.ru/vocabulary...
- Горяйнова, Анастасия Вячеславовна Разработка и исследование метода анализа групповых автоматов, полученных переброской дуг в эталоне. – [электронный ресурс]. – http://masters.donntu.ru/2017/fknt/...
- Минимизация конечных автоматов [Электронный ресурс]. – http://mathhelpplanet.com/static...
- Изоморфизм и эквивалентность автоматов [Электронный ресурс]. – https://studfile.net/preview...
- Изоморфные автоматы [Электронный ресурс]. – https://studopedia.ru/5...
