Реферат за темою випускної роботи
Зміст
- ВВЕДЕННЯ
- 1. ОСНОВНІ ПОНЯТТЯ ТЕОРІЇ АВТОМАТІВ
- 1.1 Планування станів та їх переходів
- 1.2 Реалізація простого кінцевого автомата
- 1.3 Використання кінцевого автомата
- 1.4 Наведені автомати
- 2. МІНІМІЗАЦІЯ АВТОМАТІВ
- 3. ПОСТАНОВКА ЗАВДАННЯ
- 4. ПРИКЛАДИ
- ВЫСНОВОК
- ПЕРЕЛIК ПОСИЛАНЬ
Вступ
Теорія автоматів як наукова дисципліна виникла в межах теорії керуючих систем (теоретичної кібернетики) в середині ХХ століття, в період почався бурхливий розвиток засобів електронної обчислювальної техніки і відповідних областей математичного знання.
Потрібна була розробка теоретичної бази для вирішення проблем, що виникали при проектуванні реальних цифрових ЕОМ, а також в процесі побудови і дослідження гіпотетичних систем, таких як нейронні мережі. В якості моделей останніх розглядалися кінцеві автомати.
Розвиток інформаційних технологій вивело сферу застосування теорії автоматів далеко за рамки моделювання апаратних засобів цифрової електроніки, розширивши її до фундаментальних основ сучасної теоретичної інформатики.
Сьогодні абстракції і моделі, розроблені в теорії автоматів, затребувані такими науковими дисциплінами як теорія формальних граматик, математична лінгвістика, теорія логічних моделей, математична логіка і формальні аксіоматичні системи, теорія кодування, теорія обчислювальної складності та іншими.
Найбільш тісно теорія автоматів пов'язана з теорією алгоритмів і, зокрема, з таким її розділом як теорія абстрактних машин.
В даний час існує ряд видань навчального та навчально–методичного призначення, в назвах яких міститься словосполучення теорія автоматів
.
Нерідко ці видання носять синтетичний характер, об'єднуючи під однією обкладинкою як елементи самої теорії автоматів, так і фрагменти перерахованих вище наукових областей, в яких апарат даної теорії знаходить потужне і цілком виправдане застосування.
1. ОСНОВНІ ПОНЯТТЯ ТЕОРІЇ АВТОМАТІВ
Кінцевий автомат – це деяка абстрактна модель, що містить кінцеве число станів чого–небудь. Використовується для подання і управління потоком виконання будь–яких команд. Кінцевий автомат ідеально підходить для реалізації штучного інтелекту в іграх, отримуючи акуратне рішення без написання громіздкого і складного коду [1].
Кінцевий автомат (або просто FSM – Finite–state machine) це модель обчислень, заснована на гіпотетичної машині станів. В один момент часу тільки один стан може бути активним. Отже, для виконання будь–яких дій машина повинна змінювати свій стан.
Кінцеві автомати зазвичай використовуються для організації та подання потоку виконання чого–небудь. Це особливо корисно при реалізації ІІ в іграх. Наприклад, для написання мозку
ворога: кожне стан являє собою якусь дію (напасти, ухилитися і т. д.).
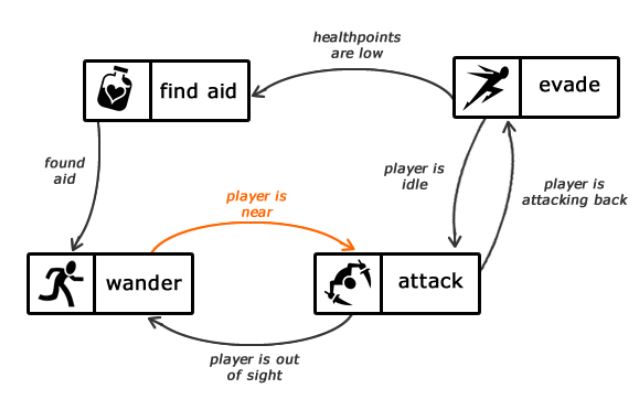
Рисунок 1.1 — Опис станів автомата
Кінцевий автомат можна представити у вигляді графа, вершини якого є станами, а ребра – переходи між ними. Кожне ребро має мітку, що інформує про те, коли повинен відбутися перехід. Наприклад, на зображенні вище видно, що автомат змінить стан wander
на стан attack
за умови, що гравець знаходиться поруч.
1.1 Планування станів і їх переходів
Реалізація кінцевого автомата починається з виявлення його станів і переходів між ними. Уявіть собі кінцевий автомат, що описує дії мурашки, що несе листя в мурашник [2].
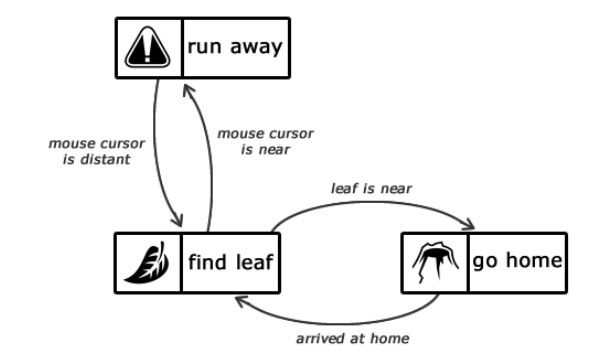
Рисунок 1.2 — Опис станів інтелекту мурашки
Відправною точкою є стан find leaf
, яке залишається активним до тих пір, поки мураха не знайде лист. Коли це станеться, то стан зміниться на go home
. Це ж стан залишиться активним, поки наш мураха не добереться до мурашника. Після цього стан знову змінюється на find leaf
.
Якщо стан find leaf
активно, але курсор миші знаходиться поруч з мурахою, то стан змінюється на run away
. Як тільки мураха буде в досить безпечній відстані від курсору миші, стан знову зміниться на find leaf
.
Потрібно звернути увагу на те, що при направленні додому або з дому мураха не боятиметься курсора миші. Чому? А тому що немає відповідного переходу.
Варто звернути увагу на відсутність переходу між run away
і go home
.
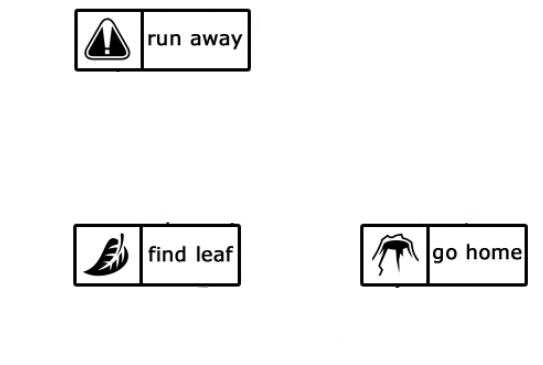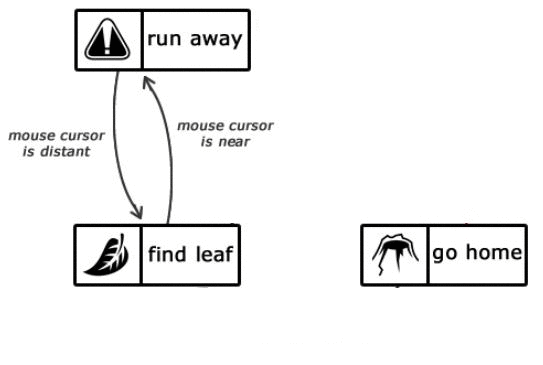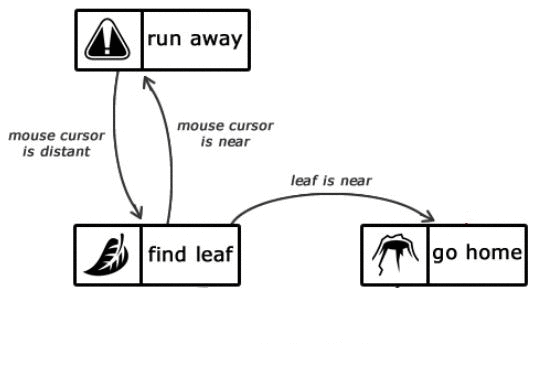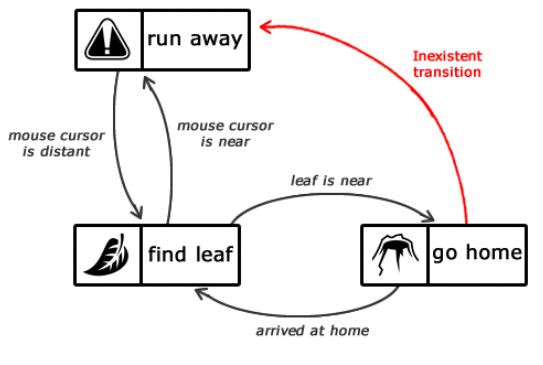
Рисунок 1.3 — Опис станів інтелекту мурашки
(анімація: 6 кадрів, 6 циклів повторення, 100 кілобайт)
1.2 Реалізація простого кінцевого автомата
Кінцевий автомат можна реалізувати за допомогою одного класу. Назвемо його FSM.
Ідея полягає в тому, щоб реалізувати кожне стан як метод або функцію.
Також будемо використовувати властивість activeState для визначення активного стану.

Рисунок 1.4 — Реалізація кінцевого автомата
Будь–яке стан є функція [3].
Причому така, що вона буде викликатися при кожному оновленні кадру гри.
Як вже говорилося, в activeState буде зберігатися покажчик на функцію активного стану.
Метод update () класу FSM повинен викликатися кожен кадр гри.
А він, у свою чергу, викликатиме функцію того стану, яке в даний момент є активним.
Метод setState () буде задавати нове активний стан.
Більш того, кожна функція, яка визначає якийсь стан автомата, не обов'язково повинна належати класу FSM – це робить наш клас більш універсальним.
1.3 Використання кінцевого автомата
Реалізуємо ІІ мурашки. Вище ми вже показували набір його станів і переходів між ними. Проілюструємо їх ще раз, але в цей раз зосередимося на коді.
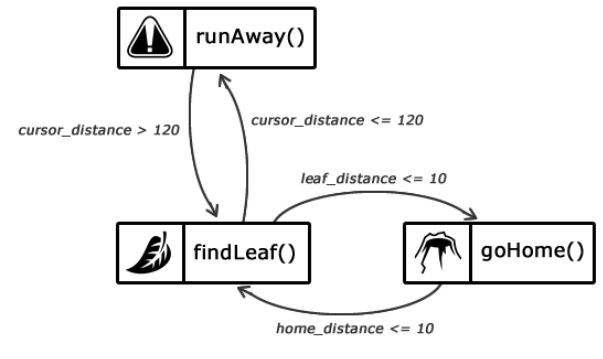
Рисунок 1.5 — Опис станів інтелекту мурашки
Наш мураха представлений класом Ant, в якому є поле brain. Це як раз екземпляр класу FSM.
Клас Ant також містить властивості velocity і position. Ці змінні будуть використовуватися для розрахунку руху за допомогою методу Ейлера. Функція update () викликається при кожному оновленні кадру гри.
Для розуміння коду ми опустимо реалізацію методу moveBasedOnVelocity (). Якщо хочете дізнатися детальніше на тему руху, прочитайте серію статей Understanding Steering Behaviors.
Нижче наводиться реалізація кожного з методів, починаючи з findLeaf () – стану, відповідального за пошук листя [4].

Рисунок 1.6 — Опис стану, відповідального за пошук листя

Рисунок 1.7 — Стан goHome ()
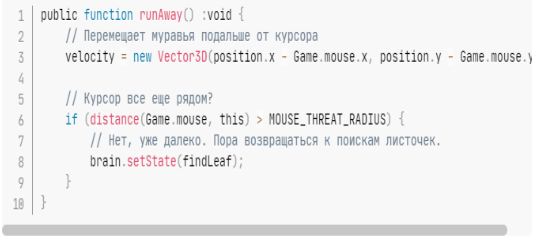
Рисунок 1.8 — Стан runAway ()
Кінцеві автомати, безумовно, корисні для реалізації логіки штучного інтелекту в іграх.
Вони можуть бути легко представлені у вигляді графа, що дозволяє розробнику побачити всі можливі варіанти.
Реалізація кінцевого автомата з функціями–станами є простим, але в той же час потужним методом.
Навіть більше складні переплетіння станів можуть бути реалізовані за допомогою FSM.
1.4 Наведені автомати
Автомат називається наведеним, якщо він не містить недосяжних станів і ніякі два його стану нееквівалентний один одному.
Якщо автомат неприведення, то можна отримати еквівалентний йому автомат з меншим числом станів або шляхом викидання недосяжних станів, або шляхом об'єднання двох еквівалентних станів в одне, як було показано в двох попередніх параграфах.
Процес приведення можна повторювати до тих пір, поки не вийде наведений автомат. Таким чином, для кожного кінцевого автомата існує еквівалентний йому наведений автомат.
Наведений автомат, отриманий таким способом, має менше число станів, ніж вихідний (якщо вихідний ні вже наведеним), і може бути більш компактно реалізований на обчислювальній машині.
Здійснюючи приведення різними способами або починаючи з різних еквівалентних автоматів, можна припустити, що отримані наведені автомати виявляться різними.
Однак ці автомати будуть фактично однаковими в усіх відношеннях, за винятком імен, якими названі їх стану.
2. МІНІМІЗАЦІЯ АВТОМАТІВ
Процес відшукання мінімальної форми називають мінімізацією автомата. Отриманий автомат називають мінімальним. Очевидно, мінімізація полягає у визначенні Pэкв подальшому побудові характеристичних функцій fs, fy автомата A з урахуванням того, що кожен клас в Pэкв – це одне стан A.
Таким чином, індивідуальне розпізнавання кожного стану вихідного автомата стає непотрібним: важливо тільки визначити, до якого класу еквівалентності воно відноситься.
Автомат можна привести до мінімальної формі різними шляхами. Одним з найбільш поширених способів мінімізації є ітераційний алгоритм Милі. Алгоритм складається з двох етапів, на яких здійснюється пошук пар еквівалентних станів. Розглянемо ці етапи.
Етап 1, крок 1. Отримання первинного розбиття.
Два стану si і sj відносимо до одного класу еквівалентності ∑1h, якщо для кожного xk ∈ X виконується рівність:
тобто при будь–якому вхідному впливі реакція автомата однакова в обох станах.
Етап 2, крок (i + 1), i ≥ 1. Ітераційне розбиття раніше отриманих класів.
Два стану su і sv, що належать одному класу еквівалентності ∑ij (номер кроку, індекс j – номер класу), відносимо до класу ∑(i+1j), якщо для кожного xk ∈ X вірно:

тобто під впливом кожного вхідного сигналу автомат, перебуваючи як в su, так і в sv переходить в стан, що належать одному і тому ж класу еквівалентності ∑iw, отриманого на попередньому кроці розбиття.
3. ПОСТАНОВКА ЗАДАЧI
Автомати, у яких характеристичні функції однакові, за винятком можливих відмінностей в позначеннях станів, називаються ізоморфними одна одній. Якщо заданий автомат М, який представляє певну систему, то будь–який автомат, ізоморфний до М, також може служити поданням цієї системи. Отже, уявлення системи автоматом ні в якому разі не єдино [7].
Якщо ми хочемо з'ясувати, еквівалентні чи автомати A1 и A2, то можна мінімізувати кожен з них. Якщо мінімальні автомати A1' i A2' мають безлічі станів з різним числом вершин, то вихідні автомати свідомо не еквівалентні. Можна довести, що вихідні автомати еквівалентні тоді A1' и A2' тільки тоді, коли відповідні їм мінімальні автомати і ізоморфні. Кінцеві автомати A1' и A2' Вважаються ізоморфними, якщо існує така біекція h безлічі станів першого автомата на безліч станів другого, яка є изоморфизмом даних кінцевих автоматів як орієнтованих графів і володіє додатково такі властивості:
1) якщо s01 – початковий стан кінцевого автомата A1', то h(s01)= s02 – початковий стан кінцевого автомата M2';
2) якщо F1 – підмножина заключних станів кінцевого автомата A1', то h(F1)= F2 – підмножина заключних станів кінцевого автомата A2';
3) для будь–яких двох станів s і t кінцевого автомата A1' будь–якого вхідного символу a маємо s → a t тоді і тільки тоді, коли h(s) → a h(t).
У загальному випадку проблема розпізнавання еквівалентності A1 и A2 зводиться до проблеми розпізнавання ізоморфізму мінімальних автоматів. Для малого числа вершин (до 10) цей ізоморфізм, як правило, розпізнається "неозброєним оком", але в загальному випадку потрібні спеціальні алгоритми.
4. ПРИМЕРЫ
Перш ніж сформулювати завдання, дамо формальне визначення ізоморфних автоматів.
Автомати А = (S(A), X, Y, δA, λA) и B = (S(B), X, Y, δA, λA) називаються ізоморфними <=> існує взаємно–однозначна відповідність φ: S(A) → S(B), що зберігає функції переходів і виходів, тобто кожен s ∈ S(A), x ∈ X: φ(λA (s,x)) = δA (φ(s),x), λA (s, x) = λA(φ(s),x).
Постановка задачі. Для заданих автоматів А = (S, X, Y, δA, λA) и В = (S’, X, Y, δA, λA), где |S|=|S’|, знайти нетривіальне безліч перекидань дуг в А, в результаті яких виходить автомат А ', ізоморфний В.
Під тривіальним безліччю перекидань розуміємо безліч, яке визначається наступним чином:
- Встановимо довільну біекція: S’ → S;
- Перевизначити дуги в автоматі А: якщо в автоматі В є дуга (s’, x, y, t’), то в автоматі А проводимо дугу (φ(s’), x, y, φ(t’)).
Зауваження. Очевидно, що для того, щоб такі перекидання були можливі, необхідно і достатньо, щоб безлічі експериментів висоти 1 у автоматів А і В збігалися, тобто WA^1=WB^1.
Розглянемо кілька прикладів побудови шуканих перекидань дуг.
Приклад 1.
Нехай автомати А і В представлені на рис. 4.1 і 4.2.
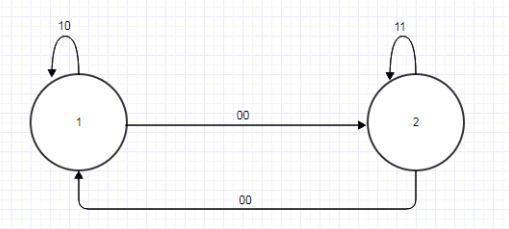
Рисунок 4.1 — Граф автомата А
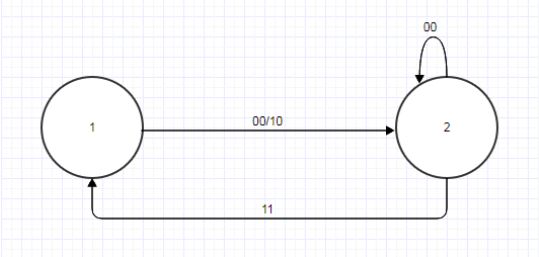
Рисунок 4.2 — Граф автомата B
Зауважимо, що безлічі експериментів висоти 1 у автоматів А і В збігаються: WA^1 = {{00,10}, {01,10}} = WB^1.
Очевидно, що в результаті перекидання стан 1 в А 'має бути еквівалентно станом 1' в У, а стан 2 в А '– станом 2' в В.
Очевидно, що для цього необхідно перекинути три дуги:
- (1, 1, 0, 1)замінюємо дугою (1, 1, 0, 2) (перекидання дуги в стан 2;
- (2, 1, 1, 2) – (2, 1, 1, 1) (перекидання в стан 1);
- (2, 0, 0, 1) – (2, 0, 0, 2) (перекидання в стан 2).
Результат перекидання зображений на рис. 4.3.
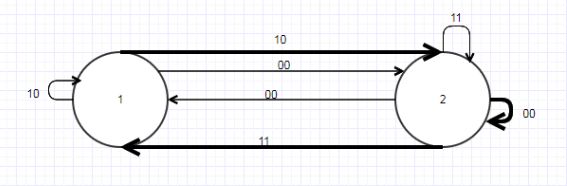
Рисунок 4.3 — Автомат А’
В результаті перекидання повинен бути отриманий автомат А 'ізоморфний В. Ізоморфізм автоматів може бути перевірений за допомогою алгоритму Рк – таблиця (див. Гілл) для автомата, який виходить приписуванням до автомату В автомата А'. Позначимо отриманий автомат А'uВ.
Розглянемо послідовний процес побудови Рк – таблиць для автомата А'uВ. В процесі побудови Рк – таблиць будь–яка така таблиця повинна мати наступну властивість:
(*) Кожен її клас еквівалентності повинен містити однакову кількість станів як автомата А ', так і В.
В силу рівності WA^1=WB^1 кожен клас таблиці Р1 володіє цією властивістю. На наступному кроці, в таблиці Р2, ця властивість може бути порушено. Щоб не допустити такого порушення потрібно організувати перекидання деяких дуг. Погляньмо на цей процес на прикладах.
Приклад 2.
Рассмотрим два автомата А и В, показанные на рисунках 4.4 и 4.5:
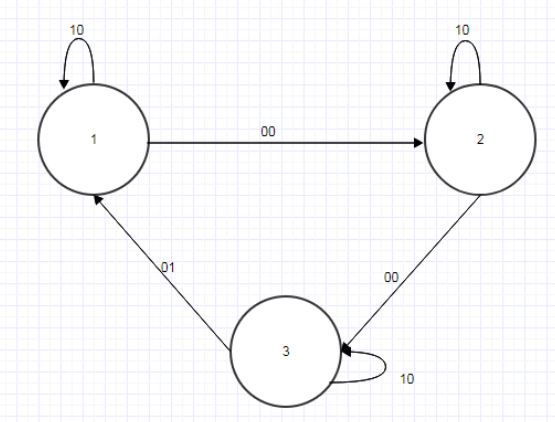
Рисунок 4.4 — Граф автомата А
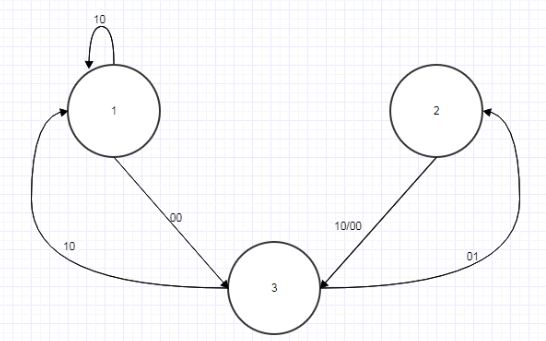
Рисунок 4.5 — Граф автомата B
Строим Рк–таблицы для А’uB (табл. 4.1, 4.2):
Таблиця 4.1 — Р2.
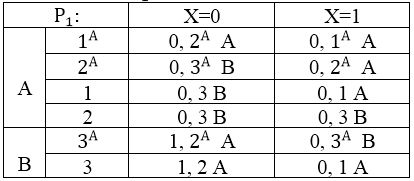
Из таблицы Р1 видно, что:
- Клас В в наступній таблиці Р 2 розпадеться на два підкласу: {3}, {3^А}. Для недопущення цього необхідно дугу (3^А, 1,0,3^А) перекинути в стан, який виявиться еквівалентним станом 1 в автоматі В, тобто в стан φ(1).
- Клас А в наступній таблиці Р2 розпадеться на три підкласу: {1^А}, {2^А, 1}, {2}. При цьому властивість (*) буде порушено через класів {1^А} і {2}. Для запобігання цьому порушення потрібно об'єднати стану 1^А і 2 в Р 2. Це можна зробити перекиданням двох дуг: заміною (1^А, 0, 0, 2^А) на (1^А, 0, 0, ? (3)) і (1^А, 1, 0, 1^А) на (1^А, 1, 0, (3)).
Таблиця 4.2 — Р2.
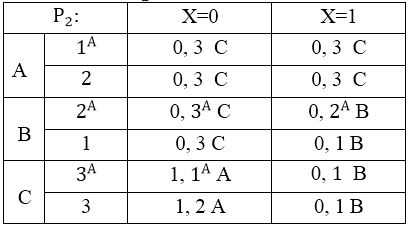
З таблиці Р2 видно, що автомат А 'ізоморфний В, так як кожен клас містить по одному стану з А' і В.
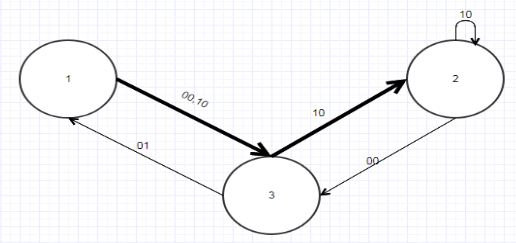
Рисунок 4.6 — Граф автомата А’
Приклад 3.
Нехай автомати А і В представлені на рис. 4.7 і 4.8.
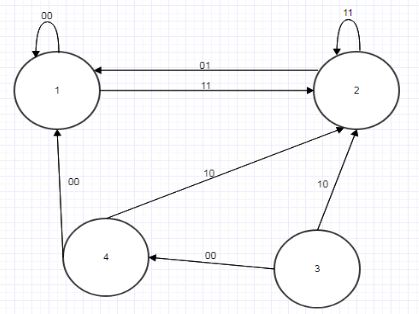
Рисунок 4.7 — Граф автомата А
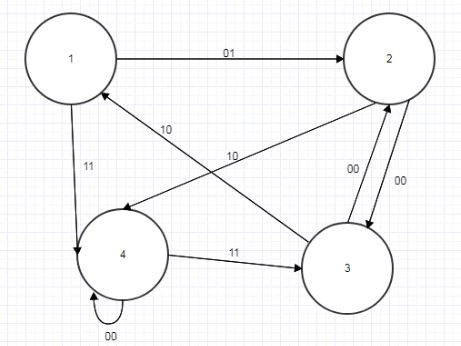
Рисунок 4.8 — Граф автомата В
Будуємо Рк – таблиця для А’uB (табл. 4.3, 4.4):
Таблиця 4.3 — Р2.
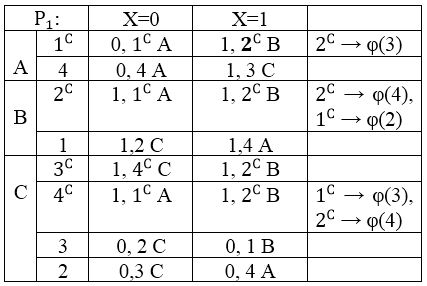 2">
2">
З таблиц Р1 видно, що:
- Клас В в наступній таблиці Р2 розпадеться на два підкласу: {3}, {3^А}. Для недопущення цього необхідно дугу (3^А, 1,0,3^А) перекинути в стан, який виявиться еквівалентним станом 1 в автоматі В, тобто в стан φ(3).
- Клас А в наступній таблиці Р2 розпадеться на три підкласу: {1^А}, {2^А, 1}, {2}. При цьому властивість (*) буде порушено через класів {1^А} і {2}.
Таблиця 4.4 — Р2.
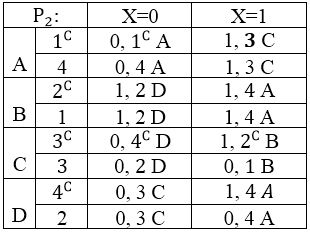 2">
2">
З таблиці Р2 видно, що автомат А 'ізоморфний В, так як кожен клас містить по одному стану з А' і В (рис. 4.9).
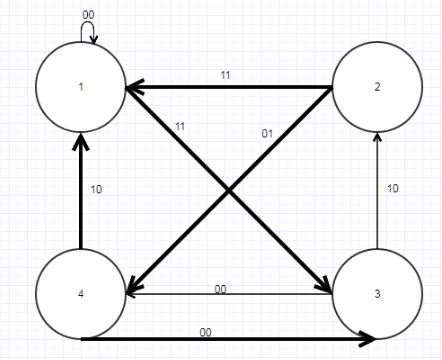
Рисунок 4.9 — Граф автомата А’
Заключение
В рамках данной работы был проведен ряд экспериментов с автоматами, которые позволяют сформулировать процедуру порождения одного автомата из другого. Данная процедура состоит в построении Рк–таблиц для автомата А’UB и переопределении перебрасываемых дуг в А’ таким образом, чтобы в процессе переброски каждый класс каждой Рк–таблицы состоял из одинакового числа состояний автомата А’ и автомата В.
Данная процедура обладает свойством недетерминизма и в последующем будет представлена в виде алгоритма.
Перелік посилань
- Брауэр, В. Введение в теорию конечных автоматов / [пер. с нем]. – М.: Радио и связь, 1987. – 392 с.
- Гуренко, В. В. Введение в теорию автоматов / В. В. Гуренко – Москва: МГТУ им. Н. Э. Баумана, 2013. – С. 4–19.
- Капитонова, Ю. В. Основы дискретной математики / Ю. В. Капитонова, С. Л. Кривий, А. А. Летичевский, Г. М. Луцкий, Н. К. Печурин. – К.: Наукова думка, 2002. – 568 с.
- Ковалев Д. В., Копытова О. М. Разработка и исследование метода построения функции деградации поведения конечного автомата в результате переброски дуг // Сборник материалов II Международной научно–практической конференции
Программная инженерия: методы и технологии разработки информационно–вычислительных систем
(ПИИВС–2018). – Донецк: ДонНТУ, 2018. – С. 230 – 233. - Буевич, В. А. Автомат конечный / В. А. Буевич [Электронный ресурс]. – Режим доступа: https://scanwordbase.ru/vocabulary...
- Горяйнова, Анастасия Вячеславовна Разработка и исследование метода анализа групповых автоматов, полученных переброской дуг в эталоне. – [электронный ресурс]. – http://masters.donntu.ru/2017/fknt/...
- Минимизация конечных автоматов [Электронный ресурс]. – http://mathhelpplanet.com/static...
- Изоморфизм и эквивалентность автоматов [Электронный ресурс]. – https://studfile.net/preview...
- Изоморфные автоматы [Электронный ресурс]. – https://studopedia.ru/5...
