Аннотация
Михно В.Ю. Обучающая система с элементами интеллекта по обыкновенным дифференциальным уравнениям первого порядка. Рассмотрены системы блочного моделирования. В статье представлен краткий обзор новой автоматизированной системы обучения по обыкновенным дифференциальным уравнениям первого порядка.
Annotation
Mikhno V. A training system with elements of intelligence for ordinary differential equations of the first order Systems of block modeling are considered. The article provides a brief overview of the new automated learning system for ordinary differential equations of the first order.
Общая постановка проблемы
В общем случае обучающие программы считаются интеллектуальными, если они обладают способностью: генерировать учебные задачи; решать задачи, предъявляемые обучаемому, используя методы представления знаний об изучаемой дисциплине; определять стратегию и тактику ведения диалога; моделировать состояние знаний обучаемого; самообучаться на основе анализа результатов взаимодействия с обучаемыми.
Таким образом, целью исследования является изучение и реализация интелектуальной обучающей системы, которая будет реализована на современной компьютерной техникие и с помощью компьютерных технологий.
Анализ архитектур моделирующих программ
Классификация интеллектуальных обучающих систем делит их на 4 типа, различающихся по составу и назначению. К первому классу относят консультационные интеллектуальные системы. Они предназначены для консультирования при решении задач и поиске информации по обучению. Данная интеллектуальная обучающая система состоит из двух сред: учебной справочной и системы объяснения. Ко второму классу относится диагностическая система обучения. Она предназначена для диагностики ошибок во время решения задач. В данную систему входят интерфейс, экспертная система по решению задач и система по диагностике ошибок и модели обучаемого. Данная система может рассматриваться в качестве дополнения консультирующей интеллектуальной системы. Третий класс представляют управляющие системы. Такие интеллектуальные обучающие системы используются для управления познавательным процессом деятельности студента курса. Система такого типа представляет собой расширенную диагностическую интеллектуальную обучающую систему с базой знаний о целях функционирования системы и стратегиях обучения по ней. Четвертым классом интеллектуальных систем считают сопровождающие системы, которые нужны для отслеживания деятельности пользователя, а также оказания ему необходимой помощи в случае, если система обнаружит ошибки в его действиях. Сопровождающая и управленческая интеллектуальные системы являются одними из наиболее сложных интеллектуальных систем обучения. Отличительными характеристиками сопровождающей системы является то, что данная система не имеет представления о цели деятельности обучаемого, и у нее есть задача спрогнозировать эту деятельность. Также данная система менее склонна к коммуникации, что позволяет пользователю меньше на нее отвлекаться.
Современные интеллектуальные обучающие системы имеют различные алгоритмы интеллектуализации. Цель их использования – проведение процесса обучения естественно-научным предметам. Они имеют функциональную возможность оценки шага процесса решения пользователя по критерию «правильно» и «неправильно». Кроме того, такие интеллектуальные обучающие системы дают возможность подсказки с указанием на неправильность шага пользователя либо на его дальнейшие действия. Неотъемлемой функцией таких систем является то, что они выставляют оценки по итогам обучения курса. При работе системы такого класса проводят проверку процесса решения пользователя на критерии завершенности и правильности. Эти критерии проверяют методом сравнения шагов решения пользователя и шагов, которые заданы в системе по умолчанию.
При реализации процесса адаптации в интеллектуальных обучающих системах одним из важнейших моментов является выбор математических методов. Анализ литературных источников позволил выделить 4 категории методов, применяемых в ИОС.
Первая категория включает методы, основанные на теории экспертных систем и реализующие построение хода курса обучения наряду с интеллектуальным анализом результата опроса обучаемого. Плюсом использования таких методов при разработке ИОС является предоставление большого круга способов анализа действий, осуществляемых экспертными системами. К минусам можно отнести сложность наполнения базы знаний и регулировки параметров экспертной системы.
Вторая категория представляет собой математические методы, использующие теорию нечетких множеств и нечеткой логики. ИОС, в которых применяются такие методы, зачастую реализуют технологию построения последовательности курса обучения. Основной особенностью таких ИОС является адаптивность процесса построения курса обучения с учетом неопределенности уровня знаний обучаемого. К недостаткам таких систем можно отнести сложность в выборе параметров алгоритмов нечеткой логики.
К третьей категории были отнесены методы на основе статистических подходов для решения задачи классификации, например, разбиение обучающихся на кластеры в зависимости от уровня предварительной подготовки.
Четвертая категория объединяет методы, основанные на теории эволюционных алгоритмов (генетические алгоритмы, искусственные нейронные сети и т.д.). Основной используемой технологией здесь является интеллектуальный анализ ответов обучаемого. К особенностям таких систем относят их широкое применение в задачах адаптивного контроля знаний. В качестве недостатка выступает отсутствие единого способа обоснования принимаемых решений в искусственных нейронных сетях, и проблема сходимости генетических алгоритмов.
Для реализации идеи интеллектуальной составляющей автоматизированной системы был апробирован 1 алгоритм, относящихся к первой категории математических методов, описанных выше.
В начале работы с ЭУМК студенту предлагается пройти предтест, вопросы которого связаны с концептами, подразделами и разделами этого учебно-методического комплекса. После окончания теста система анализирует вопросы, отвеченные студентом неверно, и предлагает ему один из материалов для изучения, по которому имеются пробелы в знаниях. Затем предлагается пройти тест по этой теме. При успешном прохождении теста система предлагает следующий неизученный материал и тест по нему, в противном случае материал предлагается прочитать еще раз. Так происходит до тех пор, пока студент не изучит все требующиеся темы и не ответит правильно на все вопросы тестов.
Рассмотрим интеллектуальную составляющую в ИОС на примере одного раздела из курса дифференциальные уравнения первого порядка, такую как, дифференциальные уравнения с разделяющимися переменными. Реализация взаимодействия пользователя с системой будет описана пошагово в развернутом виде.
Для начала студенту предлагается пройти предтесты, вопросы которого связаны с концептами, правилами, теорией и решить несложные уравнения по данной подтеме.
Система оценки прохождения предтеста выглядит таким образом, что если на 50% вопросов отвечено неверно. Такой результат говорит о необходимости изучения всех тем, поэтому после нажатия на линк «Вернуться к ЭУМК» будут предложены материалы по первой теме и тест по ней. В случае верных ответов на все вопросы произойдет переход ко второй теме и т.д. В противном случае система предложит повторно изучить учебные материалы и еще раз пройти тест. Процесс будет продолжаться до получения верных ответов. Таким образом, верные ответы на все вопросы по изучаемым темам будут являться доказательством, что темы изучены.
Разберем предтест по теме дифференциальные уравнения с разделяющимися переменными.
Для начала будет предоставлен тест по теоретическому материалу, а затем практическая задача на решение несложного уравнения.
Например, уравнение может иметь форму простейшего уравнения в дифференциальной форме.
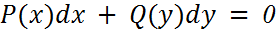
Также система сообщит студенту, чтобы он решал уравнение последовательно, в ином случае решение будет не засчитано. Система будет следить за ходом решения данного уравнения.
Как должно выглядеть решение? Студент должен объяснить, что для решения данного уравнения, необходимо проинтегрировать его полностью, взять интеграл слева, взять интеграл справа.

Далее записать общее решение уравнения с разделенными переменными.

И если будет возможность из данного уравнения выразить y, тогда нужно будет это сделать, если нет, уравнение должно будет остаться в неявном виде.
При каких условиях интеллектуальная составляющая будет рекомендовать материал для изучения?
Исходя из обработки ответов на предтесты, количество правильных и неправильных вариантов ответов, например:
- на все вопросы теста отвечено верно – в этом случае система выдавала результат, что все темы ЭУМК изучены, ничего повторять не надо;
- на все вопросы теста отвечено неверно – в данном случае автоматизированная система предлагает заново изучить все темы ЭУМК;
- только на часть вопросов получены верные ответы – в таком случае обучающая система выдает результат в зависимости от правил обучающей выборки и сложности вопросов.
На данный момент существует множество систем моделирования. Анализ научно-технической литературы показывает, что наиболее популярными являются системы моделирования DyMoLa, Dynast, Multisim, VisSim, МВТУ, MVS, SimuLink[1] Для сравнения при изучения гармонических колебаний были выбраны специализированные системы SimuLink и МВТУ.
Программный комплекс «МВТУ»[3] предназначен для исследования динамики и проектирования самых разнообразных систем и устройств. По своим возможностям он является альтернативой аналогичным зарубежным программным продуктам Simulink, VisSim и др. Удобный редактор структурных схем, обширная библиотека типовых блоков и встроенный язык программирования позволяют реализовывать модели практически любой степени сложности, обеспечивая при этом наглядность их представления. ПК «МВТУ» успешно применяется для проектирования систем автоматического управления, следящих приводов и роботов-манипуляторов, ядерных и тепловых энергетических установок, а также для решения нестационарных краевых задач (теплопроводность, гидродинамика и др.). Он широко используется в учебном процессе, позволяя моделировать различные явления в физике, электротехнике, в динамике машин и механизмов, в астрономии и т.д. Отличительной особенностью комплекса является возможность функционировать в многокомпьютерных моделирующих комплексах, в том числе и в режиме удаленного доступа к технологическим и информационным ресурсам.
Выводы
Исходя из всего выше сказанного и основываясь на своем понимании данного вопроса, я считаю, что внедрение интеллектуальности в автоматизированные обучающие системы в электронно-вычислительную технику, а в также автоматически обучающие системы – безусловно, необходимый, прогрессивный и немаловажный шаг в развитии и усовершенствовании нынешней системы образования, которая, по моему мнению, нуждается в преобразовании и реконструкции. Я считаю, что данный процесс неотвратим, а поэтому следует принимать его как неотъемлемую часть научно-технических преобразований, происходящих в нашем обществе. Для повышения мотивации обучаемого и включения в процесс обучения системы самоконтроля, его активного участия в учебном процессе и оценки знаний необходимо изменить сам подход к проблемам оценки получаемых знаний, а также увеличивать мотивацию обучаемых. Таким образом, новейшие технологии требуют изменения мировоззрения на традиционные методы использования ПК в системах контроля и доступа к информационным ресурсам, а также в организации всего учебного процесса. Все это возможно осуществить с помощью автоматизированных обучающих систем с внедрением интеллектуализации, уменьшив до минимума необъективный человеческий фактор.
Список использованной литературы
1. Попова Ю. Б. Интеллектуальная составляющая автоматизированной системы обучения CATS. Научная статья. 2019. https://cyberleninka.ru/...
2. Алешева Л. Н. Интеллектуальные обучающие системы. Научная статья. 2018. https://cyberleninka.ru/article/...
3. Макаренко С. И. Интеллектуальные информационные системы. Учебное пособие. 2009. http://window.edu.ru/...
4. Єльсгольц Л. Є. Дифференциальные уравнения и вариационное исчисление. 1969. http://www.phys.nsu.ru/balakina/...
5. Информационно-коммуникационные технологии в образовании [Электронный ресурс]. – Современные тенденции в кластерном анализе. В.Б. Бериков, Г.С. Лбов. 2018. https://biocomparison.ucoz.ru/_ld/0/49_berikov_lbov.pdf