Українська   English
ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

В связи с быстрыми темпами развития промышленного производства в XX веке добыча полезных ископаемых из земных недр достигла высокого уровня, что привело к накоплению огромных объемов горной массы в отвалах.

К составу горной массы можно отнести углесодержащие вскрышные (при открытой добыче угля) и шахтные породы, т.е. месторождения горнодобывающей индустрии техногенного характера, образующиеся в процессе добычи полезных ископаемых. В данный момент нет необходимых сведений о ежегодных масштабах образования и складирования в отвалах подобных объемов горной массы.

Современное складирование шахтных пород в отвалах не предусматривает их качественных (по минеральному и химическому составу) и механических (гранулометрический состав, сегрегацию, углы естественного откоса при разной крупности пород) характеристик. Таким образом, затрудняется использование породных отвалов, а также их утилизация. Не возможно сполна применить земельный отвод под отвалы, так как технологические схемы отсыпки отвалов не предусматривают сегрегацию пород. При выемке шахтных пород и их складировании в отвалах не предусматривается литологический состав пород, и не уточняются места их расположения в отвале. [6]

При исследовании шахтных отвалов изучается степень вреда, которую они приносят, а также возможности использования пород, химический состав и механические свойства, которые в большинстве случаев неизвестны. Таким образом, появилась необходимость разработать метод складирования шахтных пород в отвалах с учетом их литологического и химического состава, геомеханических параметров во взаимосвязи с планируемым порядком выемки угольных пластов.

Породные отвалы подлежат исследованию, так как они вызывают высокую экологическую вредность и опасность для городов и населенных пунктов. Кроме того, отвалы занимают значительные земельные площади, которые могут быть востребованы в дальнейшем при достаточном уровне развития техники и технологии.

Отвальные породы представляют интерес как источник вторичного минерального сырья. Горная порода содержит полезные ископаемые и чем старее отвалы, тем богаче они полезными ископаемыми, так как развитие технологий позволяет разрабатывать не кондиционные запасы полезных ископаемых.

В настоящее время шахта работает как новое структурное подразделение. Через определенный период времени, когда угольное предприятие ликвидируется, возникнет ряд вопросов относительно трудоустройства людей и благоустройства территории на поверхности шахты. Таким образом, возникает необходимость уже в настоящее время готовить шахту как предприятие с новой экономической направленностью, а именно, как решать вопрос с кадрами и, конечно, как использовать вторичные продукты горного производства - породные отвалы. [1]

Таким образом, научное обоснование параметров рационального планирования формирования отвалов с целью последующего (возможного) использования как техногенного месторождения является актуальной научно-технической задачей.

1. АНАЛИЗ СУЩЕСТВУЮЩИХ МЕТОДОВ ПРОСТРАНСТВЕННОЙ ИНТЕРПОЛЯЦИИ

1.1 Интерполяция и аппроксимация функций

Под интерполяцией понимают способ нахождения промежуточных значений величины по уже имеющемуся дискретному набору известных значений.

Интерполяция позволяет решать различные задачи численного анализа такие, как дифференцирование и интегрирование функций, поиск нулей и экстремумов и т. д.

Основной целью интерполяции является поиск значений таблично заданной функции в тех точках внутри данного интервала, где эта функция не задана. Исходными табличными данными могут как экспериментальные значения, так и значения, найденные расчетным путем по сложным зависимостям.

Под аппроксимацией понимают подмену исходной зависимости какой-либо достаточно простой или легко вычисляемой функцией.

Основной задачей аппроксимации является построение приближенной (аппроксимирующей) функции, которая наиболее близко проходит около данных точек или около данной непрерывной функции.

Кусочно-линейная интерполяция основывается на вычислении дополнительных точек по линейной зависимости. Графически это подразумевает простое соединение многих точек отрезками прямых. [8]

Сплайн-интерполяция основывается на проведении кривой через набор точек таким образом, чтобы первые и вторые производные кривой были непрерывны в каждой точке. Такая кривая образуется в результате формирования ряда кубических полиномов, которые проходят через наборы из трёх смежных точек. Кубические полиномы будут состыковываться друг с другом, чтобы образовалась одна кривая. Линия, описывающая сплайн-функцию, напоминает по форме гибкую линейку, которая закреплена в узловых точках.

Для описания поведения пространственно-распределенных явлений используется понятие пространственная переменная, являющаяся числовой переменной Z = Z(X, Y), которая принимает значение в произвольной точке области исследования; X, Y - координаты точки в пространстве (на плоскости).

Значения данных переменных обычно известны лишь в некоторых точках исследуемой области (рис. 1 (а)). Такие точки называются точками выборки (точками измерений, точками наблюдений, постами, выборочными точками). [9]

Рис. 1.1

где (X0, Y0) – координаты произвольной точки в области исследования, Z0 – неизвестное значение изучаемой переменной Z в этой точке, –интерполяционная оценка неизвестного значения Z0, получаемая на основе выборочных данных (Z1, Z2,…,Zn).

Для оценки значения переменной Z в точке, где она не измерена, применяются различные методы пространственной интерполяции. Выделяют два основных подхода к интерполяции: детерминированный и геостатистический. Методы детерминированной интерполяции обеспечивают аппроксимацию неизвестной переменной параметрической функцией, чья форма задается либо явно (например, полином), либо неявно (условие минимальной кривизны).

Для представления результатов пространственной интерполяции применяется прямоугольная регулярная сетка, в узлах которой вычисляется интерполяционная оценка изучаемой переменной. Таким образом, в качестве точки (X0, Y0) рассматриваются узлы этой сетки. Данное представление называется моделью пространственной переменной (рис. 1 (б)).

Расстояние между узлами сетки задается меньше размера изучаемого пространственного явления, а сама сетка полностью покрывает территорию исследования.

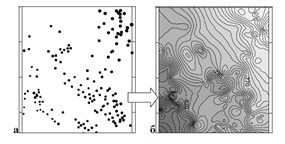
Рис. 1.2

Рисунок 1.2 – Выборочные данные (а) и пространственная модель (б)

1.2 Постановка задачи

Таким образом, в ходе исследования существующих методов анализа пространственной интерполяции были сформулированы следующие задачи:

  1. сформировать модель построения породного отвала;
  2. в соответствии с программным пакетом SURFER выбрать метод для построения пространственной модели породного отвала и провести анализ данного метода;
  3. на основе проведенного анализа интерполяции имеющихся методов из списка программного пакета SURFER выделить наиболее значимые, оценить их значение на основании экспертной оценки;
  4. на базе построенной разработанной модели предложить и решить задачу, чтобы показать основные аспекты работы с ней;
  5. на основании исследования различных источников предложить возможные решения для построения пространственных моделей породных отвалов, используя существующие программные пакеты, в том числе ГИС-технологии.

2. ВЫБОР И ОБОСНОВАНИЕ ПРОГРАММНО-МАТЕМАТИЧЕСКОГО АППАРАТА ДЛЯ СОЗДАНИЯ ГЕОМЕТРИЧЕСКОЙ МОДЕЛИ ПОРОДНОГО ОТВАЛА

Автоматизация геолого-маркшейдерских работ неразрывно связана с применением компьютерных технологий. В состав компьютерных технологий входит: сбор и обработка исходных данных, их анализ, установление корреляционных связей и зависимостей, синтез на этой основе качественно новых данных и пр. С каждым последующим этапом решения конкретной задачи встаёт вопрос выбора наиболее эффективных средств обработки информации. Большим приоритетом пользуются «стандартные» пакеты и программы, которые не всегда являются действительно эффективными.

Для решения таких задач применяется математическое и программное обеспечение геоинформационных систем типа ArcView, MapInfo, AutoCad, Easy Trace и т.п.

Программа SURFER достаточно распространенная, достаточно дешевая и простая в освоении, а также стала стандартом для других программ, о чем говорит включение формата файлов SURFER в программы других производителей. SURFER разработана в 1983 г. американской фирмой Golden Software, Фирма основана на разработке пакетов научной графики.

SURFER обеспечивает построение и визуальное проектирование двумерных карт, которые описываются функцией вида z=f(x, y). В состав функций данного пакета входит:

  1. проектирование цифровой модели поверхности;
  2. дополнительные операции с цифровыми моделями;
  3. визуальное отображение поверхности.

Постановка задачи построения карты включает в себя вычисление значений функции в любой точке области картирования по исходному набору данных.

Для осуществления перехода к значениям в регулярной сетке решаются такие задачи:

  1. построение непрерывной поверхности, позволяющей узнать значения параметра в любой точке карты;
  2. представление этих данных в виде математической цифровой модели, позволяющей решать другие метеорологические задачи.

В качестве математической основы пакета SURFER выделяют восемь алгоритмов интерполяции: Кригинг, минимизация кривизны, инверсные расстояния, полиномиальная регрессия, радиальные базовые функции, метод, триангуляция. Данные алгоритмы позволяют решать широкий круг задач. Например, триангуляция используется для построения трехмерной поверхности по точным значениям данных геодезической съемки, а алгоритм полиномиальной регрессии - для анализа тренда поверхности. Расчет регулярной сетки производится для файлов наборов данных X, Y, Z любого размера, а сама сетка имеет размеры 10000 узлов. Можно построить поверхности для функций, которые заданы в явном виде.

Основными элементами отображения являются следующие типы карт: карта изолиний (Contour Map); трехмерное изображение поверхности (3D Surface Map); карта исходных данных (Post Map, Classed Post Map); карта основы (Base Map).

Все карты редактируются с помощью встроенных инструментов пакета SURFER.

Так как породный отвал является пространственным объектом и его можно моделировать по различным видам геологических показателей, то для реализации литологопрогнозной характеристики отвала и для составления объемных изображений ярусов отвала был выбран программный пакет SURFER.

Для построения пространственной модели породного отвала применяется набор точек, которые находятся на поверхности породного отвала c координатами X, Y, Z, которые определяются в результате маркшейдерских съемок породных отвалов. Имея текстовый файл с набором таких точек, с помощью методов пакета SURFER, строится пространственная модель породного отвала. Для хранения значений SURFER использует собственные файлы типа GRD. С файлами можно работать для визуализации поверхности.

Графически поверхность изображается в двух вариантах: в виде карты изолиний или трехмерного изображения поверхности. В основу работы SURFER входят следующие принципы их построения:

  1. получение изображения методом наложения нескольких прозрачных и непрозрачных графических слоев;
  2. загрузка готовых изображений, которые могут быть получены в других приложениях;
  3. применение специальных инструментов рисования, ввод текстовой информации и формул для создания новых изображений, а также для редактирования старых изображений.

Для обеспечения экологической безопасности рациональное использование породного отвала, а также дальнейшая его рекультивация, предполагает создание динамической модели породного отвала. Использование данной модели позволяет провести анализ породного отвала, эксплуатация которого уже закончилась, т.е. показать изменение его поверхности во время эксплуатации, а также составить проект формирования породного отвала для новых разработок полезных месторождений.

3. СРАВНЕНИЕ РЕЗУЛЬТАТОВ АНАЛИЗА ИНТЕРПОЛЯЦИИ В ПРОГРАММНОМ ПАКЕТЕ MAPLE

3.1 Характеристика программного пакета Maple

Maple - это программный пакет, который обеспечивает аналитические вычисления на компьютере. Он содержит более двух тысяч команд, позволяющих решать алгебраические и геометрические задачи, задачи математического анализа, дифференциальных уравнений, математической физики, статистики.

Визуально интерфейс Maple похож на типичное окно Windows, состоящее из Строки названия, Основного меню, Панели инструментов, Рабочего поля и Строки состояния, а также Линейки и Полос прокрутки.

Работа в Maple основана на режиме сессии, то есть пользователь вводит предложения (команды, выражения, процедуры), а Maple воспримет их условно и обработает. Рабочее поле программы состоит из трех частей:

  1. область ввода включает в себя командные строки. Командная строка всегда начинается с символа >;
  2. область вывода включает в себя результаты обработки введенных команд в виде аналитических выражений, графических объектов или сообщений об ошибке;
  3. область текстовых комментариев включает в себя любую текстовую информацию, поясняющую выполняемые процедуры.

Текстовые строки Maple не воспринимает и никак не обрабатывает.

3.2 Возможности пакета Maple для визуализации изображения

1) Метод BSplineCurve. Этот метод предназначен для построения кривых B-сплайнов. Он может использоваться в двух формах:
BSplineCurve(xydata, v, opts)
BSplineCurve(xdata, ydata, v, opts),
где
xydata – определяется в форме [[x1, y1], [x2, y2],…, [xn, yn]]
xdata - определяется в форме [x1, x2,…, xn]
ydata - определяется в форме [y1, y2,…, yn]
v – имя независимой переменной
opts – необязательный параметр

Рис. 1.3

Рисунок 1.3 – График функции BSplineCurve


>m:=[[100,100],[200,-100],[-200,100],[100,200],[200,-200],[200,200],[-200,-200],[-200,-400],[-400,-200],[100,400],[-300,200],[300,300],[400,-200],[-400,-400],[-300,400],[400,-300],[200,-400],[300,400],[-500,300]];
> with(CurveFitting);
> f:=BSplineCurve(m, u);
> plot(f,u);
> plot(f,coords=polar);
>plot3d(-200/3+400*(x-6)^2-800/3*(x-6)^3,x=-400..400,y=-400..400);



2) Метод LeastSquares.
Этот метод предназначен для реализации аппроксимации по методу наименьших квадратов. Он может использоваться в двух формах:
LeastSquares (xydata, v, opts)
LeastSquares (xdata, ydata, v, opts),
где
xydata – определяется в форме [[x1, y1], [x2, y2],…, [xn, yn]]
xdata - определяется в форме [x1, x2,…, xn]
ydata - определяется в форме [y1, y2,…, yn]
v – имя независимой переменной
opts – необязательный параметр

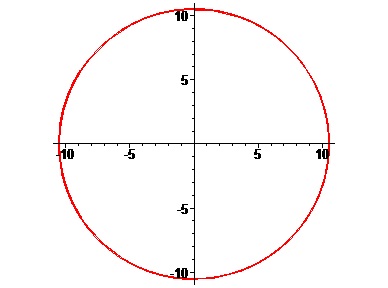
Рис. 1.4

Рисунок 1.4 – График функции LeastSquares


> f:=LeastSquares(m, u);
> plot(f,u);

4. ПОСТРОЕНИЕ МОДЕЛИ ПОРОДНОГО ОТВАЛА С УЧЕТОМ АНАЛИЗА ПОГРЕШНОСТИ ВЫЧИСЛЕНИЯ

Контурная карта породного отвала была построена на основе массива исходных данных. В качестве метода интерполяции был выбран самый оптимальный метод построения породного отвала, полученный в ходе анализа вычисления погрешностей (Табл. 2.1).

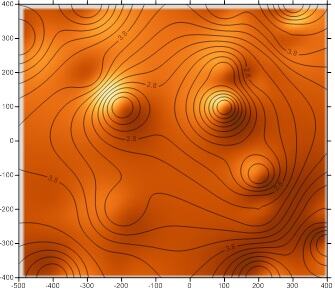
Рис. 1.5

Рисунок 1.5 – Контурная карта с отмывкой

Аналогично с контурной картой для построения применялся массив исходных данных и оптимальный метод построения породного отвала. 3D карта породного отвала строится при помощи пункта меню Map>New>3D Surface.

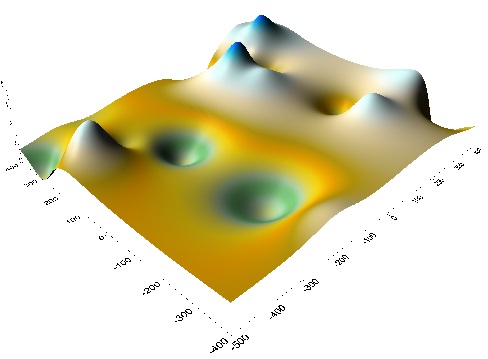
Рис. 1.6

Рисунок 1.6 – 3D карта в цветном виде

ЗАКЛЮЧЕНИЕ

В ходе выполнения дипломной работы построены контурные карты на основе разработанной модели с использованием всех методов пространственной интерполяции при помощи программного пакета SURFER, а также проведен анализ использованных методов.

В процессе анализа интерполяции проведены расчеты, в соответствии с которыми выделены наиболее значимые методы и выполнена оценка их значений на основе экспертной оценки.

На основании построенных карт и анализа погрешностей был выбран оптимальный метод для построения пространственной модели породного отвала, такой как метод обратных расстояний, который наиболее точно описывает поверхность отвала.

Таким образом, данный метод можно брать за основу для построения породного отвала.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

  1. Прокопенко Е.В. К вопросу о геометризации терриконов угольных шахт/Борщевский С.В., Прокопенко Е.В., Торубалко Д.Т//Проблемы недропользования:междунар. форум-конкурс мол.уч-ных., 21-23 апр. 2010 г. – Санкт-Петербург, 2010. – С.169-171.
  2. Прокопенко Е.В. Определение опасных экологических очагов породных отвалов/Борщевский С.В. Прокопенко Е.В., Масло С.В., Платоненко М.В.//Перспективы развития Восточного Донбасса/Шахтинский ин-т (филиал) ЮРГТУ (НПИ). – Новочеркасск: ЮРГТУ, 2010. – С.228-233.
  3. Мальцев К.А., Мухарамова С.С. Построение моделей пространственных переменных (с применением пакета Surfer): Учебное пособие. – Казань: Казанский университет, 2014. – С.103.
  4. Миронов А.И. Об экологических проблемах при закрытии шахт и путях их решений/Миронов А.И., Ткачук Н.В Уголь Украины. 2000. - С. 739.
  5. Прокопенко Е.В., Юрко Ю.С. Выбор и обоснование программно-математического аппарата для создания геометрической модели породного отвала. Материалы студенческой секции X Международной научно-технической конференции «Информатика, управляющие системы, математическое и компьютерное моделирование» (ИУСМКМ - 2019). – Донецк: ДОННТУ, 2019. – С.47–50.
  6. Прокопенко Е.В. Определение качественного состава пород по пластам для размещения в отвалах с применением линейного программирования/Борщевский С.В., Прокопенко Е.В., Гончаренко В.В.//Перспективы развития горного дела и подземного строительства. Сб. научн. трудов. Вып 2. – Киев: Предприятие УВОИ «Помощь», 2010. - С.185-188.
  7. Грядущий Б.А. Угольные месторождения Украины как источник углеводородного топлива/Грядущий Б.А., Майдуков Г.Л., Пивняк Г.Г. - Уголь Украины. - 2008. - С.3-7.
  8. Прокопенко Е.В. Создание хронолитологической модели для формирования породного отвала/Борщевский С.В., Прокопенко Е.В., Литвинова Д.С.//Материалы 5-й международной научно-практической конференции молодых ученых, аспирантов и студентов по направлению «Перспективы освоения подземного пространства» (7-8 апреля, НГУ, Днепропетровск), 2011. - С.20-23.
  9. Прокопенко Е.В. Комплексный подход к формированию породных отвалов в угледобывающих регионах/Борщевский С.В., Масло С.В./Материалы IV научной конференции «Агошковские чтения», 12 ноября 2011 г. - Чита: ЗабГК, 2011. - С.85-93.