Лопатин А.А. Современное состояние проблемы математического моделирования и прогнозирования эпидемического процесса / А.А. Лопатин, В.А. Сафронов, А.С. Раздорский, Е.В. Куклев // Проблемы особо опасных инфекций, вып. 105, 2010 [Ссылка]
УДК 616.9-036.2
Современное состояние проблемы математического моделирования и прогнозирования эпидемического процесса
А.А. Лопатин, В.А. Сафронов, А.С. Раздорский, Е.В. Куклев
Приведен краткий систематизированный обзор методов моделирования в медицине и эпидемиологии, в частности, – описание отдельных отечественных и зарубежных примеров использования математического моделирования и прогнозирования эпидемического процесса.
Ключевые слова: математические модели, математическое и компьютерное моделирование эпидемий.
С начала 20 века в эпидемиологии получили широкое распространение математические модели, построенные на феноменологии эпидемического процесса типа SIR и различных его модификациях, которые можно в известной мере отнести к детерминированным моделям. [1] Начиная с работ О.А.Барояна, Л.А.Рвачева и Ю.Г.Иванникова [2, 3, 6], в практику отечественной эпидемиологии вошли математические модели, построенные на основе феноменологии эпидемического процесса типа SEIRF (S – восприимчивые, E – индивидуумы, находящееся в инкубации, – индивидуумы с клиническими проявлениями инфекционной болезни, R – выздоровевшие, F – умершие). Данный подход был успешно применен для моделирования эпидемии и пандемии гриппа на территории СССР и современной России [2, 3, 4, 6]. Современные математические модели на основе указанного феноменологического подхода претерпели ряд изменений математического аппарата и были адаптированы для других видов инфекционных болезней.
Известно, что назначение систем математического моделирования и прогнозирования с феноменологией типа SEIRF состоит в получении количественного прогноза развития эпидемического процесса, что обеспечивает:
- оценку эффективности различных комплексов мер противодействия развитию эпидемического процесса при ЧС в области санитарно-эпидемиологического благополучия населения, включая террористические акты с применением патогенных биологических агентов, по различным сценариям;
- научно-обоснованную оперативную оценку возможного экономического ущерба при возникновении эпидемии особо опасных болезней с учетом мер противодействия эпидемическому процессу при различных начальных условиях;
- оценку готовности медицинских служб к ликвидации последствий чрезвычайных ситуаций в области санитарно-эпидемиологического благополучия населения, включая расчет необходимого количества средств индивидуальной защиты, лекарственных препаратов, средств экстренной профилактики, лабораторной базы и др.
В РосНИПЧИ «Микроб» совместно с ГУ НИИЭМ им. Н.Ф.Гамалеи РАМН были разработаны математические модели эпидемии с феноменологией эпидемического процесса типа SEnImRF, вызванной возбудителем чумы в условиях крупного города с учетом мер противодействия развитию эпидемического процесса [5]. Математические модели реализованы в комплексе компьютерных программ. Опираясь на анализ архивных и литературных данных, разработаны наиболее вероятные сценарии развития эпидемического процесса в условиях крупного города. Расчеты, проводимые по этим программам, позволяют оперативно, опираясь на минимальные исходные данные, дать количественный прогноз развития эпидемической ситуации, оценку возможному экономическому ущербу, возможности ликвидации эпидемии силами и средствами местного здравоохранения. Например, рассматривая возможность применения возбудителя чумы в качестве биологического агента при террористическом акте в крупном городе, можно оперативно провести расчеты динамики количества заболевших людей с учетом таких мер противодействия эпидемическому процессу, как изоляция и экстренная профилактика, а также расчеты количества необходимых препаратов для экстренной профилактики населения (рис. 1).
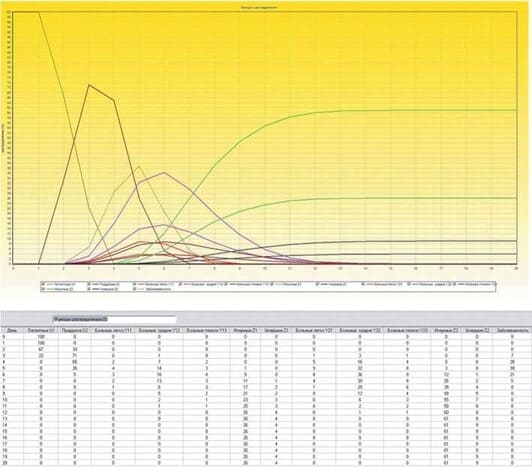
Рисунок 1 – Результаты вычислений в программном комплексе, визуализированных при помощи графиков и таблиц
Математические модели с феноменологией эпидемического процесса типа SIR и SEIR c учетом пространственной взаимосвязи были использованы в разработке программного обеспечения STEM (Spatiotemporal Epidemiological Modeler) корпорацией IBM (рис. 2). Пространственные и временные взаимосвязи реализованы при помощи математического аппарата и теории графов [7]. С учетом численности населения на каждой из территорий, географических и макроэкономических данных, дорожных карт, расположения аэропортов, транспортной системы, маршрутов миграции птиц программа составляет графическую презентацию возможных путей и динамики распространения инфекции. Основным преимуществом является возможность интеграции в разработанную IBM стандартизованную инфраструктуру Public Health Affinity Domain (PHAD).
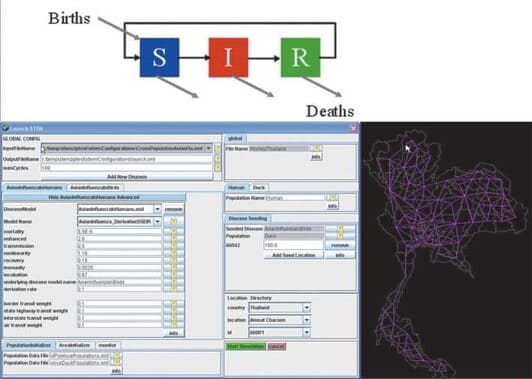
Рисунок 2 – Структура модели типа SIR. Интерфейс программы. Визуализация пространственных связей
Программа STEM разработана IBM в рамках международной инициативы по борьбе с возникновением эпидемий вроде птичьего гриппа, в которой участвуют более двадцати организаций здравоохранения по всему миру. STEM подходит для работы с любой операционной системой и построена на открытом исходном коде, поэтому программу можно «подгонять» для работы с распространением самых разных вирусов, а результаты расчетов визуализировать при помощи, например Google Earth [9].
Развитие информационных технологий в последние годы, использование в научных исследованиях технологий распределенных вычислений, использование «суперкомпьютеров» позволили пересмотреть подходы к моделированию эпидемий. Один из таких подходов в моделировании и прогнозировании эпидемического процесса использовался в эпидемиологической модели EpiSims [8].
EpiSims в качестве основы использует разработанную ранее TRANSIMS – модель оценки последствий реорганизации транспортной инфраструктуры города Портленд штат Орегон. Анализируя официальные данные, на карте выделили 180 тыс. узловых точек и составили картину повседневной жизни 1,6 млн виртуальных жителей Портленда. Это позволило создать адекватную картину физических контактов между людьми в больших населенных пунктах (рис 3).
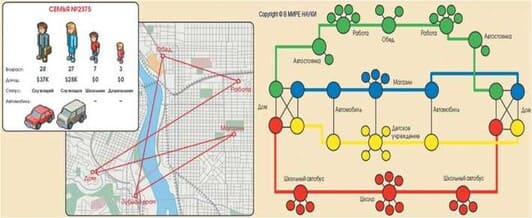
Рисунок 3 – Иллюстрация построения социальной сети в EpiSims
В созданной модели, на протяжении 100 дней, была промоделирована вспышка оспы по нескольким сценариям с учетом мер противодействия и без. Результаты моделирования показали, что определяющим фактором противодействия распространению инфекции является время начала мероприятий. Также результаты расчетов показали, что массовая вакцинация населения в данном случае нецелесообразна. Гораздо более эффективна избирательная вакцинация при условии ранней регистрации эпидемии. Важно также и введение карантина.
Чтобы оценить стоимость и результативность различных мероприятий, авторы смоделировали преднамеренное распространение легочной чумы в Чикаго. Оказалось, что отслеживание контактов инфицированных, прекращение занятий в учебных заведениях, введение в городе закрытого режима сопряжено с миллиардными убытками и дает мало преимуществ по сравнению с таким относительно недорогим мероприятием, как массовый прием антибиотиков [10].
Таким образом, анализ доступных литературных источников показал, что в эпидемиологии используются самые различные методы математического моделирования. В зависимости от целей можно использовать достаточно простые детерминистические или
стохастические модели и сложные имитационные компьютерные. Современное развитие информационных технологий позволило использовать чрезвычайно сложный математический аппарат для моделирования эпидемического процесса. Тем не менее, имеющиеся
модели либо находятся в стадии разработки, либо требуют серьезной адаптации и доработки для решения вопросов практической эпидемиологии. На данный момент из отечественных разработок для решения задач, поставленных в рамках Федеральной
целевой программы Национальная система химической и биологической безопасности Российской Федерации (2009-2013 годы)
, наиболее применимы математические модели с феноменологией эпидемического процесса типа SEnImRF, разработанные
в ГУ НИИЭМ им. Н.Ф.Гамалеи РАМН совместно с учреждениями Роспотребнадзора по ряду инфекционных заболеваний.
Работа выполнена по Государственному кон-тракту № 116-Д от 11.06.2009 г. в рамках федеральной целевой программы >Национальная система химической и биологической безопасности Российской Федерации (2009-2013 годы)
.
Список литературы
- Андерсон Р, Мэй Р. Инфекционные болезни человека. Динамика и контроль: пер. с англ. М.: Мир, Научный мир; 2004. С. 784.
- Бароян О.В., Рвачев Л.А. Иванников Ю.Г. Моделирование и прогнозирование эпидемий гриппа для территории СССР. М.; 1977. С. 546.
- Бароян О.В., Рвачев Л.А. Математика и эпидемиология М.: Знание; 1977. С. 63.
- Боев Б.В. Новые информационные технологии в эпиде-миологии: системное моделирование процессов инфекционной патологии [автореф. дис. ... д-ра тех. наУк]. М.; 1992. 43 с.
- Кутырев В.В., Куклев Е.В. Храмов В.Н., Лопатин А.А. Математическое моделирование и прогнозирование эпидемий (вспышек) чумы в чрезвычайных ситуациях природного и тех-ногенного характера. В кн.: Противочумные учреждения России и их роль в обеспечении эпидемиологического благополучия на-селения страны. М.; 2004. С. 24-6.
- Рвачев Л.А. Моделирование медико-биологических про-цессов в обществе как раздел механики сплошных сред. Докл. АН СССР. 1972; 203(3):540-2.
- Татт У. Теория графов. Пер. с англ. М.: Мир; 1988. 424 с.
- Эпидемии [Электронный ресурс] – Режим доступа: http://www.ccs.lanl.gov/ccs5/apps/epid.shtml – Загл. с экрана.
- An extensible spatial and temporal epidemiological modelling system [Электронный ресурс] – Режим доступа: http://www.ij-healthgeographics.com/content/5/1/4#IDA XGFYC. – Загл. с экрана.
- Информация [Электронный ресурс] - Режим доступа: http://www.sciam.ru/2005/6/inform.shtml – Загл. с экрана.
A.A.Lopatin, V.A.Safronov, A.S.Razdorskiy, E.V.Kouklev Current State of Problem of Mathematical Modeling and Prognosis of the Epidemic Process. Short systematic review on the modeling methods in medicine and epidemiology is presented. In particular, special native and foreign examples of application of mathematical modeling and prognosis of epidemic process are described.
Keywords: mathematical models, mathematical and computer modeling of the epidemics.