Аннотация
А.Е. Винник. Моделирование процесса движения меканум-робота на основе построения собственных карт. Приведены результаты моделирования процесса движения четырехколесного меканум-робота с использованием метода тангенциального избегания и алгоритма быстрого исследования случайного дерева.
В статье рассматривается модель четырехколесного меканумробота, колеса которого расположены в 2 ряда вдоль стороны прямоугольного корпуса. Для решения задачи управления движением робота до заданной точки выбран метод тангенциального избегания [1], так как данный метод рассчитан на вычисление линейной и угловой скорости робота в заранее неизвестном пространстве или в пространстве с динамически меняющимся окружением.
Математическая модель робота описывается следующим образом (рис. 1):
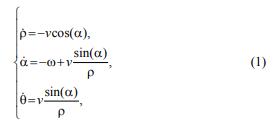
где ρ – дистанция до цели, ν – линейная скорость робота, ω – угловая скорость робота; θ – угол между осью OX и направлением на цель; α – курсовой угол, разность между курсом робота и углом θ; ψ – курс робота.
При таком описании математической модели, следует, что полностью управлять роботом можно с помощью изменения значений угловой и линейной скоростей, поэтому следует найти такие их значения, при которых достигаются условия ρ→0 и α→0. Для этого воспользуемся функцией Ляпунова в виде
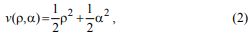
а производная по времени

не должна быть положительна.
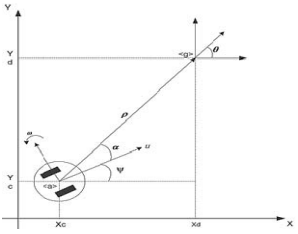
Рисунок 1 – Математическая модель
Выразим производную (3) через модель (2):
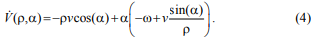
В качестве управляющего воздействия выберем следующие значения скоростей:
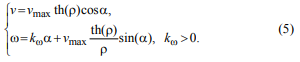
Управление движением колес меканум-робота осуществляется путем регулирования угловой скорости вращения каждого колеса. Для получения данных значений воспользуемся расчетными формулами для каждого колеса:
В процессе своего движения робот может попасть в тупик. Чтобы справиться с данной проблемой было принято решение строить карту местности в процессе движения. Для ускорения поиска маршрута до заданной точки используется алгоритм быстрого исследования случайного дерева (RRT) [2].
Моделирование процесса движения робота проводится в программном продукте, позволяющем симулировать поведение робота в закрытом пространстве с возможностью появления препятствий в процессе движения робота. В качестве языка разработки программы был выбран высокоуровневый язык программирования Python. Данный программный продукт позволяет симулировать движение робота к целевой точке при отсутствии препятствий, при наличии статических препятствий и при динамически добавляющихся препятствиях.
При движении робота в некотором изолированном пространстве не всегда известна планировка и точные координаты размещенных препятствий. Для того, чтобы приведенные выше алгоритмы движения робота работали верно в данных условиях было принято решение о построении собственной карты пространства роботом. Данная карта заполняется информацией приходящей с датчиков робота, а именно на основе показаний с дальномера и датчика цвета. На основе получаемых данных на карту можно заносить координаты увиденных препятствий и целевых объектов.
Построенную такую методом карту можно использовать в качестве исходных данных для расчета траектории и управляющего воздействия. Симуляция данного движения отображена на рис. 2, 3.
Результаты проведенной симуляции свидетельствуют о том, что алгоритмы построения дерева, поиска кратчайшего пути, следования по найденному пути работают корректно. Построение роботом небольших карт местности позволяет ему не быть привязанным к знанию местности. Однако, построение карт будет потреблять через мерное количество ресурсов, если пространство, в которое помещен робот, будет неограниченным. Данную проблему можно решить путем создания карт, небольшого пространства вокруг самого робота.
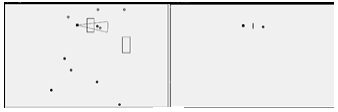
Рисунок 2 – Симуляция движения
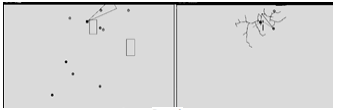
Рисунок 3 – Симуляция движения
Такой метод позволит роботу двигаться в любых условиях, но при этом робот не будет запоминать местность, где он уже был. Также можно заметить, что найденный путь является неоптимальным и в процессе расчета траектории движения робота не происходит поправок на формат-фактор самого робота. Данные проблемы являются задачами для дальнейшего рассмотрения.
ЛИТЕРАТУРА
1. Andre Ferreira; Flavio Garcia Pereira, Raquel FrizeraVassallo,Teodiano
FreireBastosFilho, MarioSarcinelliFilho An approach to avoid obstacles in mobile
robot navigation: the tangential escape.Programa de Pos-GraduacaoemEngenhariaEletrica. – Universidade Federal do Espirito Santo-Av. Fernando Ferrari, 514-
29.075-910. – Vitoria, ES, Brazil [Электронный ресурс]. – URL: http://www.scielo.br/scielo.php?pid=S0103-17592008000400003&script=sci_arttext
(датаобращения: 15.01.2018)
2. Nasir J., Islam F., Malik U. et al. RRT*-SMART: A Rapid Convergence
Implementation of RRT* // International Journal of Advanced Robotic Systems. –
Vol. 10, 299:2013S.
3. Moslehpour K., Jenab E.H. Siliveri, Design and Implementation of NIOS II
System for Audio Application // IACSIT International Journal of Engineering and
Technology. – October 2013. – Vol. 5, No. 5.