Аннотация
А.Е. Винник. Исследование динамики всенаправленной платформы при различных уровнях детализации моделей меканум-колёс и контактных сил. Рассматривается динамика мобильной всенаправленной платформы, оснащённой двумя парами меканум-колёс. Построены уравнения кинематики и динамики системы с учётом реальной геометрии роликов колёс и ограниченности контактных сил. Проведён сравнительный анализ динамических моделей системы. В «классической» неголономной модели колесо моделируется диском, проскальзывающим в направлении, ортогональном оси ролика; в уточнённой неголономной модели полностью учтена реальная конструкция колёс, а уравнения связей получены осреднением условий непроскальзывания роликов. Рассмотрены модели системы, в которых учитывается и реальная конструкция колёс, и проскальзывание с различными моделями контактных сил.
Введение
Объектом исследования является мобильная платформа всенаправленного движения, оснащённая меканум колёсами (шведскими колёсами или колёсами Илона [1]). На периферии каждого из них располагаются ролики, оси которых скрещиваются с осью колеса под углом 45°. Конструкция меканум-колёс позволяет оснащённому ими аппарату совершать всенаправленное движение (т.е. в любом направлении с произвольной ориентацией), например, двигаться поступательно вбок или совершать разворот на месте.
Благодаря своей мобильности и удобству парковки всенаправленные платформы используются для работы в стеснённых условиях складских, производственных и подобных помещений; создания транспортных средств для людей с ограниченными возможностями и в других целях [2].
В большинстве теоретических исследований механики всенаправленных платформ (см., например, [3-8]) реальные размеры роликов пренебрегаются, считается, что их количество бесконечно велико. Эти упрощения позволяют описать динамику системы в рамках неголономной механики и уменьшить размерность системы дифференциальных уравнений движения.
Однако, следует отметить, что некоторые особенности конструкции меканум-колёс приводят к негативным эффектам: возникновению вибраций при движении на высоких скоростях и снижению энергетической эффективности управляющих сил (см. обзор в [9]), которые могут быть изучены при повышении уровня детализации описания модели колёс и контактных взаимодействий.
В [10] проведено исследование экипажа, оснащенного тремя «классическими» омни-колёсами; рассмотрено влияние конечных размеров и инерционности роликов и ограниченности контактных сил на движение системы. В настоящей работе изучается динамика управляемого движения меканум-платформы с учетом реальной геометрии роликов, вязкого трения в сочленениях тел и кулоновским контактным трением.
Описание системы
Конкретным объектом исследования является KUKA youBot – мобильная платформа с двумя парами соосных меканум-колёс. Для этого робота создано свободное и открытое программное обеспечение, что позволяет использовать его для широкого класса научно-исследовательских и учебных задач.
Рассматривается движение мобильного робота youBot по горизонтальной неподвижной плоскости xy. Введём подвижную систему координат OXYZ (рис. 1, а). Начало этой системы координат находится в геометрическом центре O платформы; OX и OY – её продольная и поперечная оси, Z(x,X) = ψ.
Абсциссы и ординаты центров колёс Ci, (i=1,...,4) в системе координат OXYZ равны ρXi и ρYi (ρX1=ρX2=h, ρX3=ρX4=-h, ρY1=ρY3=l, ρY2=ρY4=-l). Угол между осями роликов i-го колеса и плоскостью CiZX обозначим δi (δ2=δ3=45°, δ1=δ4=-45°).
Обозначим Ki центр оси контактирующего ролика, а φi – угол его поворота вокруг оси i-го колеса (см. рис. 1, б). Поскольку на каждом колесе расположено по шесть роликов, то -30°<φi<30°. При смене контактирующего ролика φi скачкообразно изменяется на 60°.
Считая, что угол поворота i-го колеса φi отсчитывается от направления отрицательной полуоси CiZ, угол φi можно определить с помощью операции взятия остатка от деления mod по формуле φi=(φi+30°)mod(60°)-30°.
Поверхности всех роликов колеса касаются одной цилиндрической поверхности радиуса R, поэтому точка контакта Pi ролика с полом смещена относительно центра колеса Ci в направлении оси OY на величину ΔYi = Rdtgδitgφi [11, 12], где Rd=|CiKi| (рис. 1, в). Отметим, что в рассматриваемом случае геометрия роликов обеспечивает отсутствие вертикальных вибраций центра колеса при движении по полоскости.
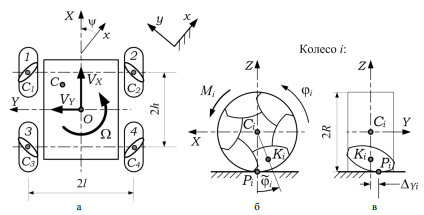
Рисунок 1 – Схема мобильной платформы; (а) – платформа, (б) – меканум-колесо, (в) – контактирующий ролик
Моделирование динамики системы
Исследуем влияние реальной конструкции меканум-колёс и ограниченности контактных сил на динамику исследуемой системы. Для этого проведём сравнительный анализ динамики нескольких моделей системы. Во всех рассмотренных моделях ролики считаются безынерционными, а в сочленениях тел действуют линейные по скоростям силы терния.
Первые две модели неголономные, проскальзывание в точках контакта отсутствует; движение системы описывается в псевдоскоростях Vx=Xocosψ+Yosinψ, Vy=-Xosinψ+Yocosψ и Ω=ψ:
Модель 1. Считается, что ролики колёс непрерывно контактируют с опорной поверхностью, а точка контакта находится на центральном поперечном сечении (т.е. φi=0). В этом случае
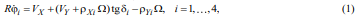
Уравнения динамики для модели 1 построены с учётом неголономных связей (1) [7]; экспериментальное определение коэффициентов в уравнениях движения проведено в [8].
Отметим, что уравнение (1) может быть получено из предположения о проскальзывании колеса, моделируемого диском радиуса R, в направлении, перпендикулярном оси контактирующего ролика [3-6].
Модель 2. Считается, что ролики колёс непрерывно контактируют с опорной поверхностью, а точка контакта перемещается по меридиану ролика. В этом случае
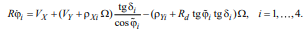
Осреднение [12] этих соотношений по углу φi даёт условия неголономных связей
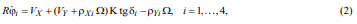
где поправочный коэффициент  .
.
Уравнения движения для модели 2 составлялись с учётом осреднённых неголономных связей (2).
В двух последних моделях учитывается проскальзывание в точках контакта роликов и опорной плоскости:
Модель 3. Силы контактного трения линейны по скорости с «большим» коэффициентом вязкости.
Модель 4. Силы контактного трения моделируются по закону Кулона.
Результаты численного решения уравнений движения для перечисленных моделей представлены на рис. 2 (номера кривых на графиках соответствуют номеру модели). Во всех четырёх случаях использовались законы изменения управляющих моментов Mi=Mi(t), при которых в соответствии с моделью 1 платформа совершает поступательное движение (ψ=π/2), а её центр O равномерно перемещается по окружности.
Для трёх других моделей траектория центра O деформируется, а платформа совершает угловые движения (см. рис. 2, б). Моделирование демонстрирует резкое возрастание контактных сил в момент переключения роликов, что может приводить к кратковременному проскальзыванию (см. рис. 2, в).
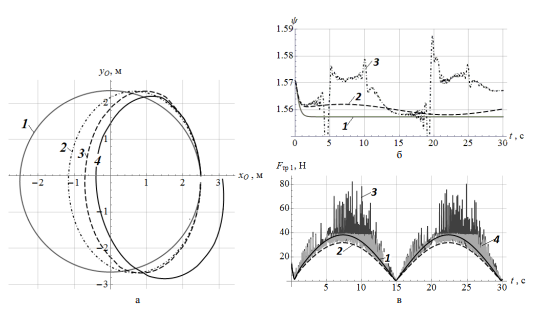
Рисунок 1 – Результаты моделирования движения платформы; (а) – траектория центра платформы, (б) – угол поворота платформы, (в) – сила трения в точке контакта ролика первого колеса
Заключение
Конструктивные особенности меканум-колёс способны существенным образом сказаться на движении мобильной платформы: помимо кратковременного проскальзывания контактирующих роликов в момент их переключения возникают систематические «уходы» обобщённых координат по сравнению со случаем, когда реальными формой и размерами роликов пренебрегают (модель 1). Учёт реальной геометрии роликов с помощью поправочных коэффициентов в уравнениях связей (модель 2) позволяет предсказать последнее свойство в рамках неголономной задачи, размерность которой существенно меньше, чем у полной задачи (модели 3 и 4).
Литература
1. B. E. Ilon. Wheels for a course stable selfpropelling vehicle movable in any desired direction on the ground or some other base.
(Patent Sweden) B60B 19/12 (20060101); B60b 019/00, REF/3876255, November 13, 1972.
2. F. Adascalitei, I. Doroftei. Practical applications for mobile robots based on Mecanum wheels — a systematic survey // The
Romanian Review Precision Mechanics, Optics & Mechatronics. 2011. No. 40. Pp. 21–29.
3. P. Muir, C. P. Neuman. Kinematic modeling for feedback control of an omnidirectional wheeled mobile robot // 1987 IEEE
International Conference on Robotics and Automation. 1987. Vol. 4. Pp. 1772-1778.
4. А. А. Зобова, Я. В. Татаринов. Динамика экипажа с роликонесущими колесами // Прикладная математика и механика.
2009. Т. 73. № 1. С. 13–22.
5. А. В. Борисов, А. А. Килин, И. С. Мамаев. Тележка с омниколесами на плоскости и сфере // Нелинейная динамика.
2011. Т. 7. № 4. С. 785–801.
6. Ю. Г. Мартыненко, А. М. Формальский. О движении мобильного робота с роликонесущими колёсами // Изв. РАН.
Теория и системы управления. 2007. № 6. С. 142–149.
7. B. I. Adamov. A Study of the Controlled Motion of a Four-wheeled Mecanum Platform // Rus. J. Nonlin. Dyn. 2018. Vol. 14.
No. 2. Pp. 265-290.
8. Б. И. Адамов, А. И. Кобрин. Идентификация параметров математической модели мобильной роботизированной
платформы всенаправленного движения youBot // Мехатроника, автоматизация, управление. 2018. Т. 19. № 3. 2018. С. 251–
258.
9. L. Xie, C. Scheifele, W. Xu, K. A. Stol. Heavy-duty omni-directional Mecanum-wheeled robot for autonomous navigation:
System development and simulation realization // 2015 IEEE International Conference on Mechatronics. 2015. Pр. 256–261.
10. К. В. Герасимов, А. А. Зобова. Динамика экипажа на омни-колесах с массивными роликами с учетом смены ролика в
контакте с опорной плоскостью // Труды МАИ. 2018. №101. С. 1-26.
11. A. Gfrerrer. Geometry and Kinematics of the Mecanum Wheel // Computer Aided Geometric Design. 2008. Vol. 25. No. 9.
Pp. 784–791.
12. B. I. Adamov. Influence of Mecanum Wheels Construstion on Accuracy of the Omnidirectional Platform Navigation (on
example of KUKA youBot Robot) // 25th Anniversary Saint Petersburg International Conference on Integrated Navigation
Systems. 2018. Pp. 251-254.