Аннотация
Б.А. Костырко. Планирование траектории движения мобильного робота с дифференциальным приводом в MATLAB. В статье описывается разработка алгоритма чистого пресле- дования при планировании траекторий движения мобильного робота с дифференциальным приводом.
Введение
Мобильные роботы находят все большее применение в условиях, когда присутствие человека в зоне выполняемых работ представляет опасность или нежелательно по соображениям ограничения производительности обслуживаемого оборудования.
Область применения мобильных роботов самая широкая: ликвидация ЧС, обслуживание торговых площадок, исследование незнакомой местности, включая другие планеты и т.д.
При этом планирование перемещения робота является важнейшей задачей автономных робототехнических систем. Решение данной задачи охватывает такие области как искусственный интеллект, вычислительная геометрия, компьютерное моделирование и теория ав- томатического управления [1].
Автоматизация процесса планирования перемещения является одной из важнейших подзадач передвижения мобильного робота. Ее можно разделить три части: построение карты, определение пути через координаты, планирование перемещения. В случае если роботу задается путь в виде n-ого количества координат x(n),y(n) задача их прохождения за минимальное количество времени напрямую связана с производительностью. При этом важным фактором является неизменность максимальных параметров линейной и угловой скорости движения робота, а также быстродействие.
Решение данной задачи напрямую связывают с использованием алгоритма pure-pursuit (чистое преследование) [2]. Подобные и другие задачи функционирования и навигации мобильных роботов не могут решаться без применения компьютерного моделирования. Так, например, в программном пакете MATLAB, начиная с версии 9.4, появилось приложение MOBILE ROBOTICS SIMULATION TOOLBOX [3], а ранее с версии 8.5 - ROBOTICS SYSTEM TOOLBOX [4]. Эти приложения позволяют быстро освоить основы планирования траекторий мобильных роботов для сокращения времени разработки прототипов устройств в условиях конкретной практической задачи.
Цель работы: изучение основных принципов функционирования алгоритма «pure pursuit» и особенностей его реализации для дифференциального привода в программной среде MATLAB.
Данный алгоритм относят к итерационному методу планирования траектории движения в области вычислительной геометрии (рис.1).
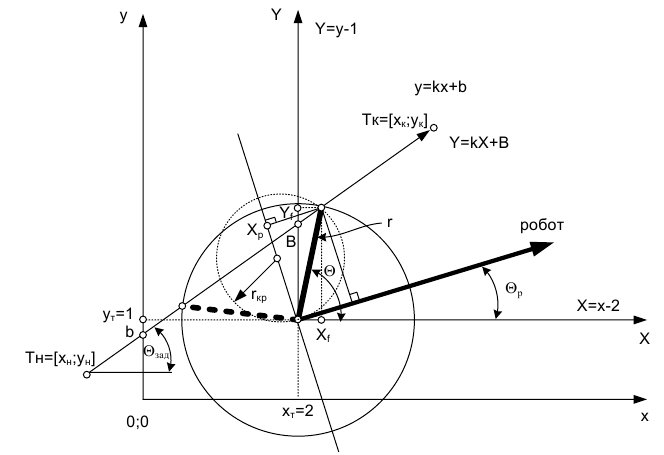
Рисунок 1 – Алгоритм чистого преследования при планировании траектории движения
Задачу планирования движения робота из начальной точки Тн с координатами [xн,yн] к конечной точке Тк [xк,yк] в текущей точке [xт,yт] можно свести к определению желаемого угла θ, при котором робот встречается с траекторией движения [Тн; Тк] на расстоянии r. Тогда при изменении угла текущей ориентации робота θр в соответствии с θ, робот автоматически приедет в точку Тк.
Из рисунка видно, что определение угла θ возможно при решении квадратного уравнения относительно [Xf,Yf] для неподвижной системы координат текущего положения робота [X,Y]. Тогда из двух полу- ченных корней квадратного уравнения выбирается тот, который находится ближе к точке Тк (рис.1).
При этом алгоритм чистого преследования работает в функции проекции точки [Xf,Yf] на вращающуюся ось абсцисс робота [2]. На рисунке 2 показано, что точка Xp может иметь отрицательное значение, тогда угловая скорость будет положительной:
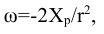
где r – дальность обнаружения точки движения по траектории. Физический смысл координаты Xр заключается в том, что она обратнопропорциональна радиусу кривизны rкр. При стремлении Xр→0, робот едет прямо, а rкр→оо.
На рисунке 2 представлен общий вид модели планирования траектории движения пяти одинаковых мобильных роботов с дифференциальным приводом при различных алгоритмах управления.
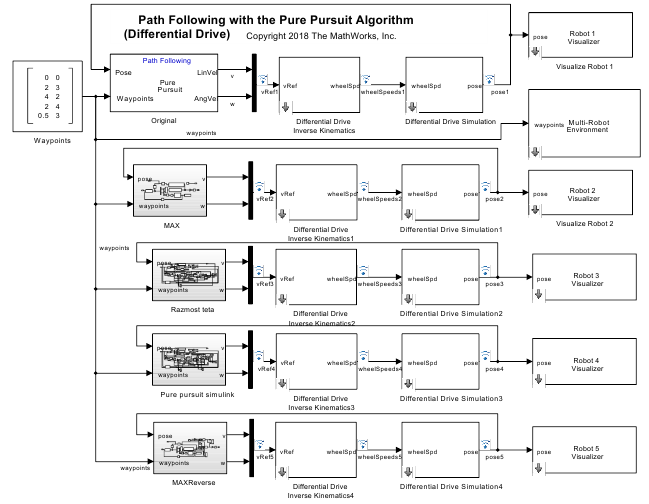
Рисунок 2 – Модель алгоритмов чистого преследования роботов с дифференциальным приводом и одинаковыми условиями
На ней блок «original» представляет собой оригинальный алгоритм, в виде блока MATLAB Pure Pursuit. Его использование не возможно для версий MATLAB ниже 8.5. Использовались параметры линейная скорость 0.5 м/с, максимальная угловая скорость 1.5рад/с, r=0.35 м.
Его выходы линейной скорости v и угловой скорости ? задаются на вход обратной кинематики дифференциального привода [2], где преобразуются в угловые скорости колеc. Блок «differntial drive simulation» состоит из прямой кинематики и перехода к вращающейся системе координат ориентированной с роботом. В ней рассчитываются линейные скорости по осям x,y и угловая скорость, которые после интегрирования дают вектор ориентации робота pose=[xт yт θр]^T.
При моделировании учитывались следующие параметры: R=0.1м – радиус колеса, L=0.5м – длина между колесами, шаг моделирования 0.05с, начальная ориентация 180°.
Недостатком алгоритма «original» является кратковременный выход угла θр в другой квадрант по отношению к углу θзад. Это приводит к увеличению пройденного пути. При этом робот описывает окружность в сторону, ближайшую к углу θзад и далее выходит на траекторию [Тн;Тк].
Аналогично робот ведет себя при достижении текущих координат (waypoints) и переключении на следующую пару координат.
Еще один недостаток предлагаемого MATLAB решения это работа только в версиях выше 15, что существенно увеличивает аппаратные требования к компьютеру для моделирования мобильных роботов.
Алгоритмы для «Pure pursuit simulink» и «Raznost teta» роботов используют расчет точки [Xf,Yf] (рис.1), и достаточно приближаются к оригинальному алгоритму, но не повторяют его (рис.3). Здесь недостатком алгоритма «Pure pursuit simulink» является кратковременный уход угла θр в другой квадрант по отношению к заданному направлению с углом θзад. Это приводит к прохождению избыточного пути. Аналогичная ситуация наблюдается в работе алгоритма «Original» с оригинальным алгоритмом при переходе от 3-ей к 4-ой точке (3-я и 4-ая строка координат waypoints на рис.1).
В соответствии с рис.1 алгоритм чистого преследования может работать в функции разности углов (θ-θр). При этом возможна настройка системы под оптимум, зависящий от шага обновления параметров, а также быстродействия контуров регулирования скорости роботов. Подобное решение допускает ограничение текущего задания θ в соответствии с квадрантом θзад.
Оба предложенные алгоритмы показали повышение быстродействия в соответствии с оригинальным (рис.3) за счет меньшего пройденного пути.
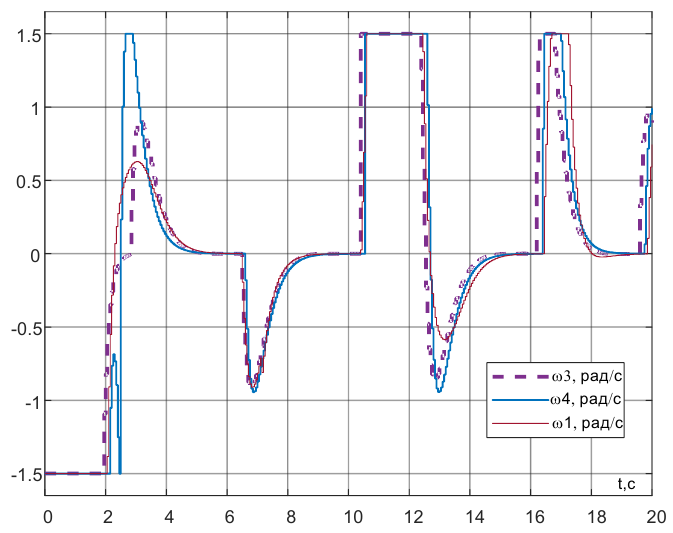
Рисунок 3 – Результаты моделирования алгоритмов чистого преследования роботов с дифференциальным приводом
Повышение быстродействия робота возможно не за счет выхода на траекторию [Тн;Тк], а с применением пересчета данной траектории по текущему вектору ориентации, когда θ=θзад, а Тн=Тт. Такой алгоритм «MAX» представлен на рисунке 2 и характеризуется минимальным пройденным путем и, как следствие, максимальным быстродействием. В этом случае робот не касается траектории [Тн;Тк].
При возможности реверсирования двигателей, наибольшее быстродействие мобильного устройства дает алгоритм «MAXReverse», в котором алгоритм «MAX» учитывает направление линейной скорости робота (рис.4,5).
Версии MATLAB выше 9.4 позволяют также производить анализ движения роботов при помощи графического интерфейса иллюстрирования вектора ориентации роботов pose.
Фрагменты вывода результатов моделирования представлены на рисунке 5.
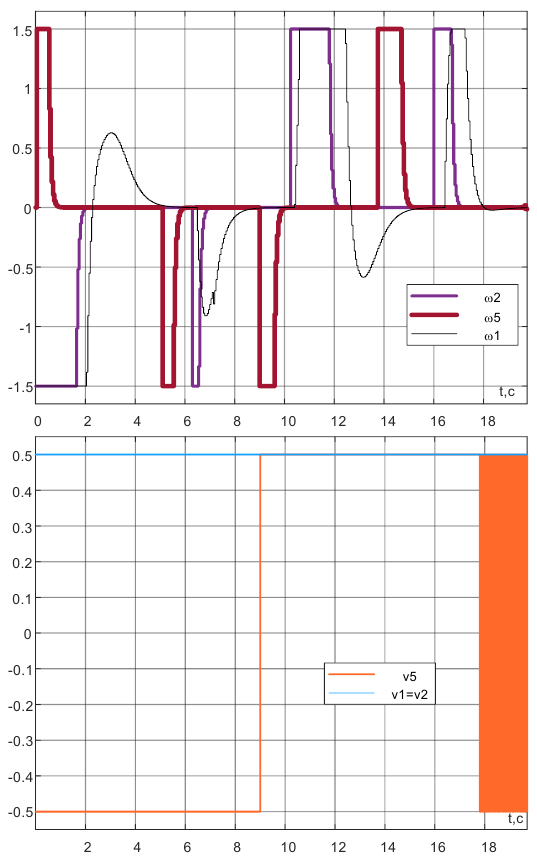
Рисунок 4 – Результаты моделирования предложенных алгоритмов управления роботами с пересчетом траектории движения
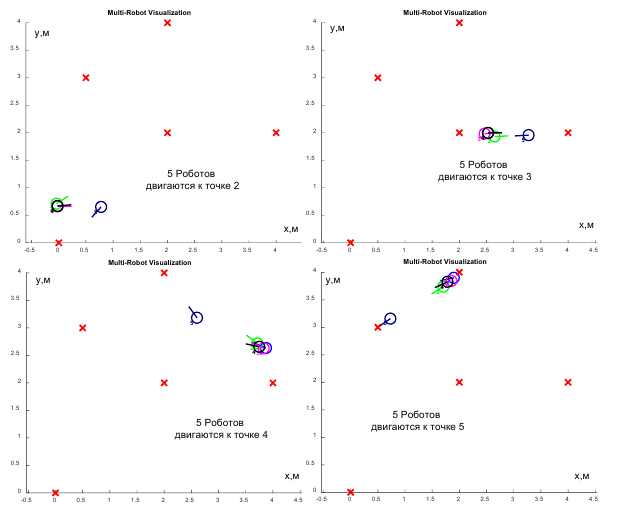
Рисунок 5 – Графическое представление движения роботов
Вывод
В работе рассмотрены алгоритмы чистого преследования позволяющие моделировать движения робота к цели с учетом ориентации. Подобные решения могут быть использованы для движущейся цели, и для низких версий MATLAB.
Перечень ссылок
1. Чинь Суан Лонг. Методы построения интеллектуальных систем планирования перемещения мобильного робота в неизвестной среде : диссертация ... кандидата технических наук : 05.02.05 / Чинь Суан Лонг; [Место защиты: Юж.-Рос.
гос. техн. ун-т (Новочеркас. политехн. ин-т)].- Новочеркасск, 2010.- 139 с.
2. Bethencourt, Julio & Ling, Qiang & Valera, Бngel. (2011). Controller design
and implementation for a differential drive wheeled mobile robot. Proceedings of the
2011 Chinese Control and Decision Conference, CCDC 2011.
10.1109/CCDC.2011.5968930.
3. Mobile Robotics Simulation Toolbox [Электронный ресурс]/ Mathworks. —
Режим доступа: https://www.mathworks.com/matlabcentral/fileexchange/66586-
mobile-robotics-simulation-toolbox, свободный. — Загл. с экрана.
4. Robotics system toolbox [Электронный ресурс]/ Mathworks. — Режим до-
ступа: https://www.mathworks.com/products/robotics.html, свободный. — Загл.
с экрана.