English
ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

Динамическая устойчивость – это свойство системы сохранять режим исходный или близкий к исходному при конечных возмущениях [1].

Динамическая устойчивость - относительное требование и она должна обеспечиваться при определенных условиях.

Анализ динамической устойчивости – это анализ режимов конечных возмущений.

Обеспечение динамической устойчивости системы электроснабжения (СЭС) позволяет существенно повышать надежность. В системах электроснабжения (ЭС) часто возникают возмущения, это связано с отключением мощных нагрузок, генераторов и трансформаторов моторов, линии электропередач (ЛЭП).

При появлении возмущения возникают переходные процессы. Эти переходные процессы могут быть при больших возмущениях и малых изменениях скорости. При больших возмущениях они состоят в следующем: проверка динамической устойчивости системы при заданных возмущениях; расчет параметров режима в течении переходных процессов с целю оценки допустимости; оценка эффективности различных разделов улучшения устойчивости [1].

Процессы при больших возмущениях и больших изменениях угловой скорости ротора, генераторов часто называют асинхронными режимами, которые включают в себе асинхронных ход, и ресинхронизацию, результирующую устойчивость.

Правильность расчетов переходного процесса во многом зависит от той точки с которой описаны основные элементы системы электроснабжения (СЭС) - в первую очередь генераторы и их системы регулирования нагрузки. Простейшем способом исследование динамической устойчивости системы электроснабжения (СЭС) является использование метода площадей, что даёт возможность получить качественную и приближенную количественную оценку условий динамической устойчивости.

Допустимые критерии и требования для динамической устойчивости устанавливаются согласно ГОСТ Р 58058-2018 [2].

В данной работе рассматривается динамическая устойчивость при больших возмущениях.


1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Динамическая устойчивость – это способность системы восстанавливать после большого возмущения исходное состояние или состояние, практически близкое к исходному (допустимому по условиям эксплуатации системы) [1].

О динамической устойчивости следует судить по характеру изменения параметров режима при конечных результатах. Изменение режима характеризуется нелинейными уравнениями, отражающими воздействие соответствующего возмущающего фактора.

В динамической устойчивости важны конкретные знания исходных условий (время, место, вид, длительность) [4-7].

Понятие устойчивости динамической системы схематически иллюстрируется примером, представленным на рис. 1.1 [1].

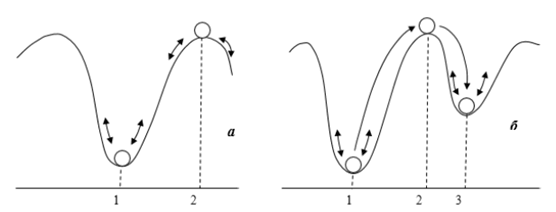
Иллюстрация понятия устойчивости динамической системы
Рисунок 1.1 – Иллюстрация понятия устойчивости динамической системы

На рис. 1.1., а положение 1 является положениям устойчивого равновесия, поскольку при отклонениях шарика от этого положения равновесия (в результате возмущения) он возвращается в положение устойчивого равновесия 1. Положение 2 является положением неустойчивого равновесия, поскольку даже при незначительном (малом) отклонении шарика (возмущении) он уходит из этого положения равновесия.

В случае малых возмущений (малых отклонений шарика от положения равновесия) говорят об устойчивости в «малом»; в ЭЭС это соответствует понятию статической устойчивости. В случае существенных больших возмущений (больших отклонений шарика от положения равновесия) говорят об устойчивости «в большом»; в ЭЭС это соответствует понятию динамической устойчивости.

В случае, если возмущение настолько велико, что нарушается динамическая устойчивость системы (шарик на рис. 1.1, б в результате такого большого возмущения отклоняется от положения равновесия 1, «проскакивает» положение неустойчивого равновесия 2 и оказывается после некоторых колебаний в устойчивом положении равновесия 3) и система оказывается в другом положении равновесия, говорят о результирующей устойчивости.


2. ОПИСАНИЕ АЛГОРИТМА МЕТОДА ПЛОЩАДЕЙ

Общая идея метода площадей состоит в сопоставлении приобретенной системой кинетической энергии на некотором интервале времени существования аварийной ситуации с запасом работы, которая может быть совершена при торможении объектов системы после ликвидации аварии. Если приобретенная кинетическая энергия в точности равна оставшемуся запасу по работе торможения, то интервал времени существования аварии полагается предельным по динамической устойчивости [4].

Рассмотрим основные процессы, а также уравнения при большом возмущении в простейшей ЭЭС [3].

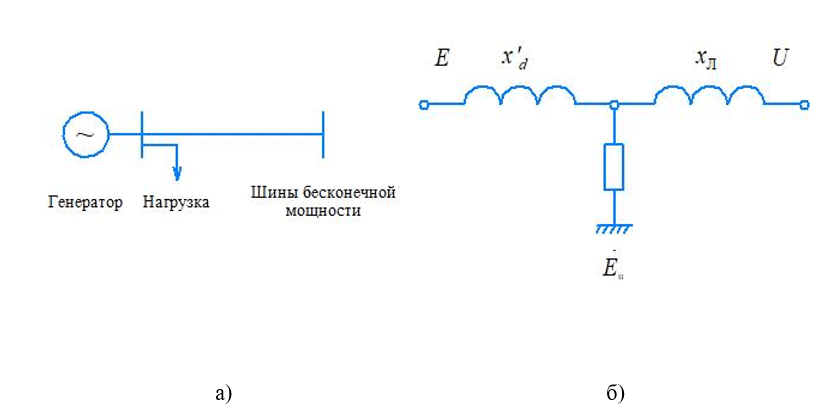
Пусть линия электропередачи на рис 2.1 включает две параллельные цепи, и одна цепь аварийно отключается по какой-либо причине. Общее сопротивление связи x=x’d+x*л увеличится, тем самым максимум угловой характеристики мощности в послеаварийном режиме окажется ниже, чем в доаварийном. Доаварийная (I) и послеаварийная (II) угловые характеристики мощности показаны на рис. 2.2, а.

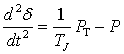
где Р – электромагнитная мощность, выдаваемая генератором, ТJ – постоянная инерции ротора генератора.

Простейшая ЭЭС (а) и ее схема замещения (б)
Рисунок 2.1 – Простейшая ЭЭС (а) и ее схема замещения (б)
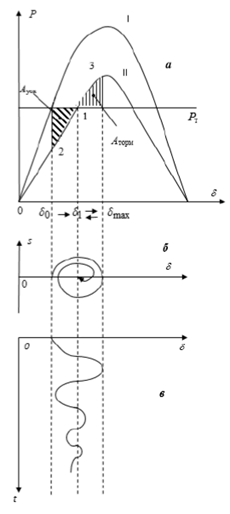
Иллюстрация поведения ротора генератора при рассмотрении динамической устойчивости ЭЭС
Рисунок 2.2 – Иллюстрация поведения ротора генератора при рассмотрении динамической устойчивости ЭЭС

В результате внезапного отключения одной цепи двухцепной линии вследствие инерции ротора в первый момент времени после возмущения мы попадаем из точки 0 угловой характеристики мощности в точку 2. В этом положении мощность турбины больше выдаваемой генератором электромагнитной мощности, т.е. ускорение имеет знак плюс и действует на увеличение угла генератора, в результате угол ротора увеличивается от значения δ0 к значению δ1.

В результате такого движения от точки 2 до точки 1 ротор набирает за счет инерционности массы ротора энергию ускорения, определяемую интегралом

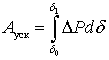
Энергия ускорения равна заштрихованной площади слева на рис. 3.1, а; она получила название площадки ускорения.

В силу инерционности ротор «проскакивает» положение равновесия 1 и движется в сторону увеличения угла ротора от значения δ1 к значению δmax. В этом диапазоне углов электромагнитная мощность генератора больше мощности турбины, небаланс мощностей отрицательный и, следовательно, ускорение ротора отрицательно, вследствие чего движение ротора тормозится и набирает энергию торможения [8].

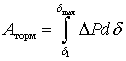
Энергия торможения ротора равна правой заштрихованной площади на рис. 3.1, а; она получила название площадки торможения.

Если потерь энергии нет, то

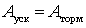
Поскольку реально потери энергии существуют вследствие трения, омических потерь и рассеяния энергии в демпферных контурах, колебания ротора постепенно затухают, что показано на рис. 2.1, б, а также траекторией угла ротора во времени (рис. 2.1, в). В этом случае динамическая устойчивость простейшей ЭЭС сохраняется.

Рассмотрим характерный случай (рис. 2.3).

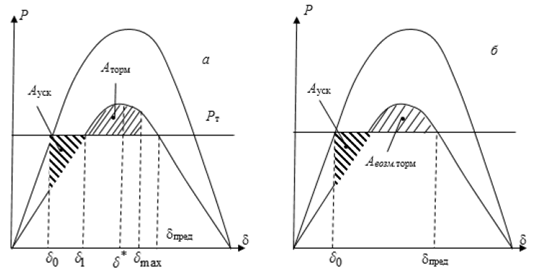
К определению энергии возможного торможения ротора
Рисунок 2.3 – К определению энергии возможного торможения ротора

На рис. 2.3, а характерно то, что ротор, компенсируя энергию ускорения энергией торможения, «пришел» к значению угла δmax>δ*, где - значение угла, соответствующее максимуму угловой характеристики мощности. Из этого следует, что ротор может набирать энергию торможения до того значения угла δпред, до которого электромагнитная мощность генератора остается выше мощности турбины. Эту потенциально возможную энергию торможения называют энергией возможного торможения (рис. 2.3, б), которая на рисунке соответствует площадке возможного торможения

Очевидно, что для того, чтобы динамическая устойчивость не нарушалась, необходимо, чтобы выполнялось условие

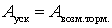
которое получило название критерия площадей, а сам метод основанный на проверке критерия, называют методом площадей.


3. ИССЛЕДОВАНИЕ СИНХРОННОЙ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ МЕТОДОМ ПЛОЩАДЕЙ

3.1 Подготовка исходных данных

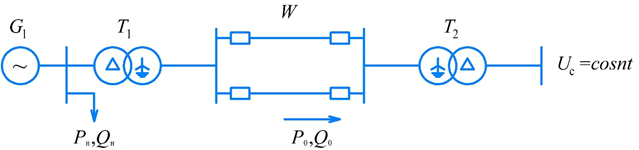
Рассмотрим методику анализа синхронной динамической устойчивости на примере простейшей электрической системы, в которой присутствуют следующие элементы: генератор, трансформаторы, ЛЭП, система и нагрузка (рис. 3.1).

Для проведения исследования было использовано программное обеспечение Mathcad, позволяющее наиболее просто осуществлять решение дифференциальных уравнений и наглядно выполнить построение графических зависимостей угловых характеристик мощности [9]. При моделировании переходных процессов во времени была применена встроенная функция «Анимация» что дает возможность, наблюдать характер переходного процесса.

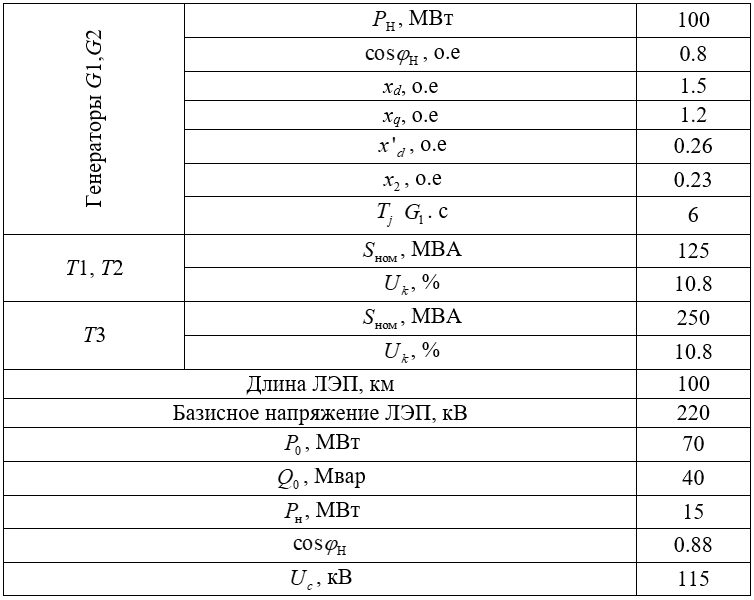
При исследовании различных режимов работы ЭЭС были использованы следующие данные об ее элементах: параметры генераторов, трансформаторов и ЛЭП. Указанные исходные данные приведены в табл. 3.1. Для выполнения опытов эти данные были внесены в расчетный файл в среде Mathcad, что показано на рис. 3.2.

Таблица 3.1 – Исходные данные

Исходные данные
Схема простейшей электрической системы
Рисунок 3.1 – Схема простейшей электрической системы
Исходные данные в программе <i>Mathcad</i>
Рисунок 3.2 – Исходные данные в программе Mathcad

Целью данного исследования является освоение методики анализа синхронной динамической устойчивости простейшей электрической системы на основе интегрирования дифференциального уравнения движения ротора, исследование влияния демпфирования и постоянной инерции ротора на характер переходного процесса. В ходе исследования были рассмотрены следующие вопросы:

1. Определение максимального значения мощности и соответствующего значения угла, при которых сохраняется синхронная динамическая устойчивость при возмущении, вызванном отключением одной цепи двуцепной ЛЭП;

2. Анализ влияния коэффициента демпфирования Pd и постоянной инерции ротора Tj генератора на указанные в п.1 параметры и характер переходного процесса;

3. Анализ влияния нагрузки, которая подключена к шинам генератора на указанные в п.1 параметры.

Для анализа протекания указанных выше процессов было проведено моделирование различных режимов работы ЭЭС. В результате были получены графичиеские зависимости, описывающие характер протекания переходных процессов. Подробные результаты представлены в п.3.3-3.9.

3.2 Опыт 1

Данный опыт проводился без изменения исходных данных системы, а также при отсутствии влияния демпфирования, т.е. Pd=0. На рисунке 3.3 показана граница устойчивости для данного случая, а также параметры искомых величин.

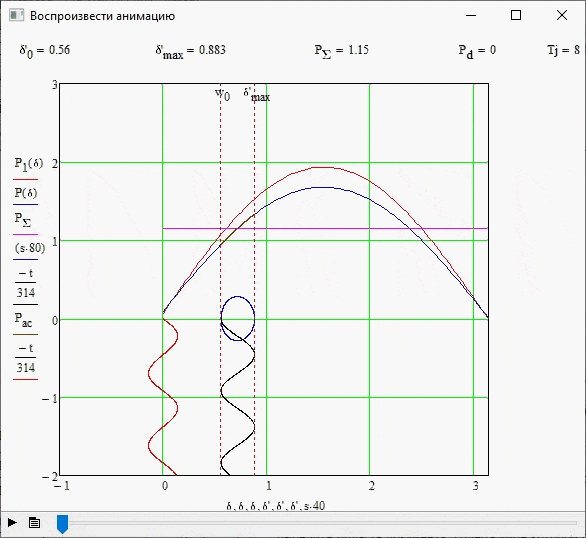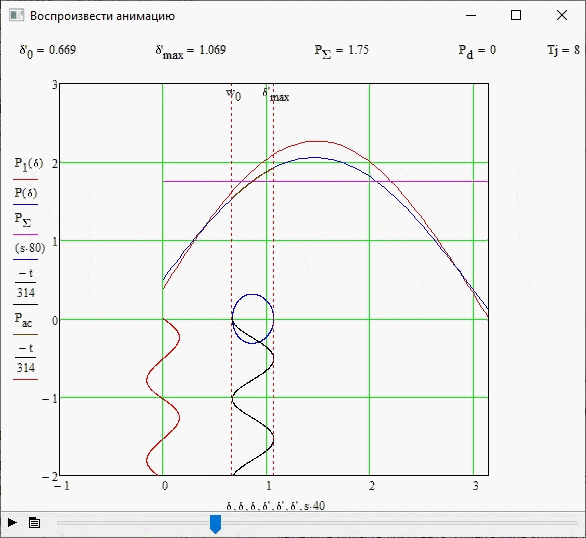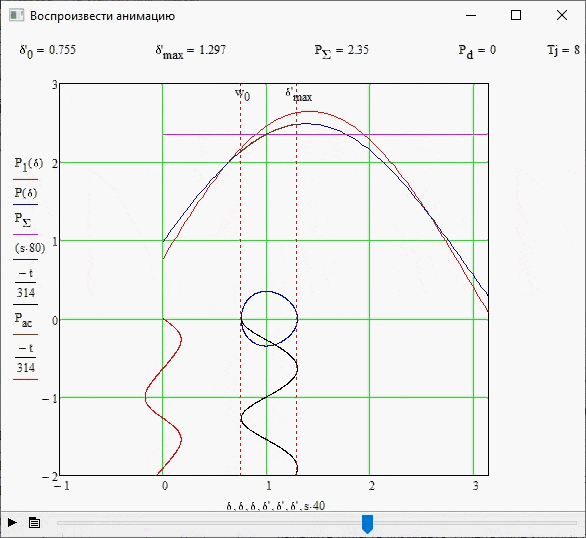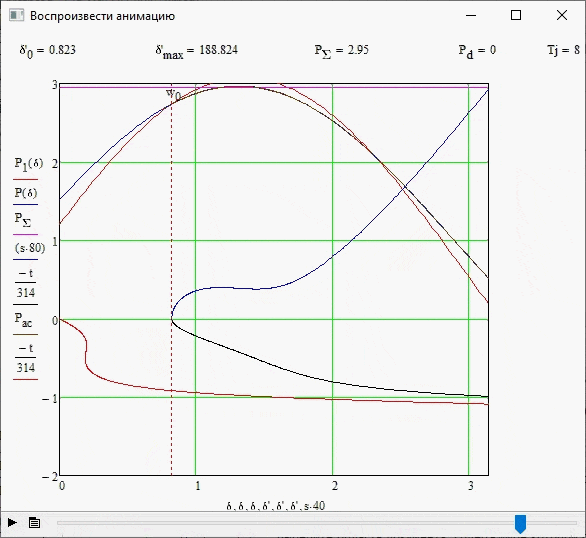
Граница устойчивости системы без влияния демпфирования
Рисунок 3.3 – Граница устойчивости системы без влияния демпфирования
Количество кадров - 7; количество циклов - 6; размер - 130 Кб.

3.3 Опыт 2

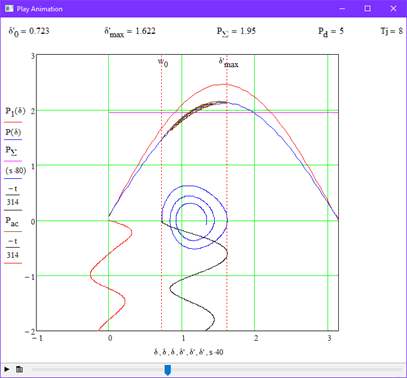
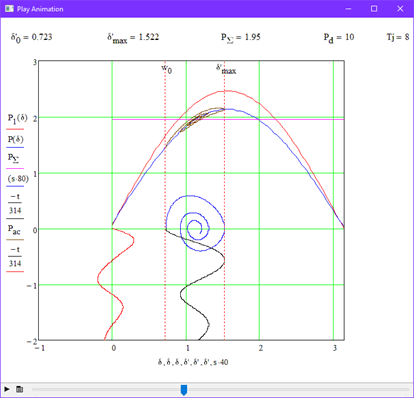
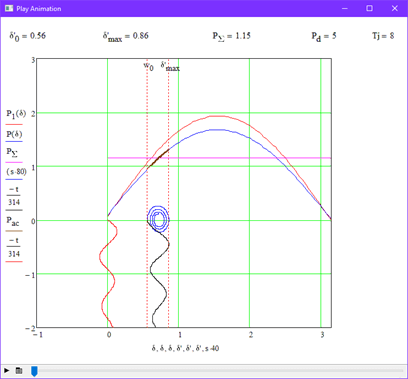
В данном опыте было проведено исследование влияния мощности демпфирующей обмотки на устойчивость системы. На рис. 3.3 показана граница устойчивости при Pd=5. Для наглядности повторим опыт, но при увеличим значение коэффицента демпфирования в 2 раза, т.е. Pd=10 (рис 3.5).

Граница устойчивости при <i>P<sub>d</sub></i>=5
Рисунок 3.4 – Граница устойчивости при Pd=5
Граница устойчивости при <i>P<sub>d</sub></i>=10
Рисунок 3.5 – Граница устойчивости при Pd=10

3.4 Опыт 3

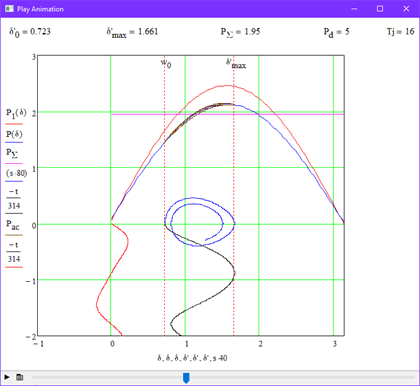
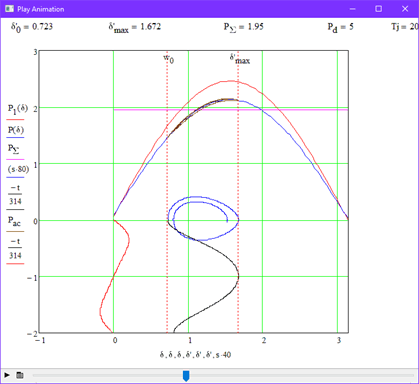
В данном опыте было рассмотрено влияние механической постоянной инерции генератора на характер переходного процесса. Для этого были заданы различные значения параметра Tj при неизменном значении демпфирования Pd=5. На рис. 3.6 показана граница устойчивости при Tj=16, а на рис. 3.7 – при Tj=20.

Граница устойчивости при <i>T<sub>j</sub></i>=16
Рисунок 3.6 – Граница устойчивости при Tj=16
Граница устойчивости при <i>T<sub>j</sub></i>=20
Рисунок 3.7 – Граница устойчивости при Tj=20

3.5 Опыт 4

В данном опыте было рассмотрено влияние на переходный процесс нагрузки, подключенной к шинам генератора. Для этого были заданы различные значения мощности нагрузки на шинах системы Pнг. Результирующие графики представлены на рис. 3.8 и 3.9.

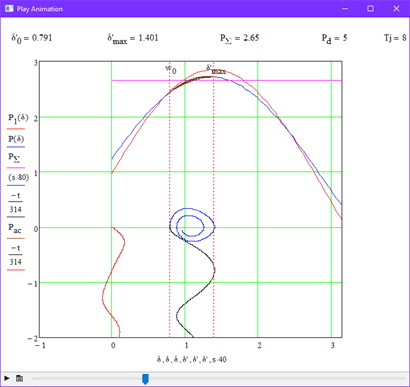
Граница устойчивости системы
Рисунок 3.8 – Граница устойчивости системы
Граница устойчивости системы
Рисунок 3.9 – Граница устойчивости системы

3.6 Анализ результатов исследования

Выполнив анализ полученных графиков, можно выделить следующие основные моменты:

1. Для нерегулируемой системы устойчивость нарушается при углах больше, чем 90° [10].

2. Добавление демпфирующей обмотки позволяет ускорить затухание колебательного процесса в роторе.

3. На пределы устойчивости увеличение Tj также не влияет, но, как и Pd, позволяет уменьшить количество колебаний в роторе.

4. Повышение мощности нагрузки, подключенной к генератору, позволяет значительно расширить границы устойчивости системы.


ВЫВОДЫ

В данной работе были рассмотрены основные теоретические положения динамической устойчивости электроэнергетической системы.

Выделены ключевые теоретические моменты по алгоритму метода площадей для проведения последующих опытов.

Было выполнено моделирование переходных процессов во времени с использованием программы Mathcad.

Поставленные задачи выполнены в полном объеме.


СПИСОК ЛИТЕРАТУРЫ

  1. Эрнет А.Д., Электромеханические переходные процессы в электрических системах: Курс лекций. – Нижневартовск: Изд-во НВГУ, 2013 – 130 с.
  2. Готман Н.Э., Шумилова Г.П., Старцева Т.Б. Идентификация топологии электрической сети на основе искусственных нейронных сетей с использованием векторных измерений // Методические вопросы исследования надежности больших систем энергетики: актуальные проблемы надежности систем энергетики: сб. докл. Междунар. науч. семинара им. Ю.Н. Руденко. Минск: Белорусский национальный технический университет, 2015. С. 251-257.
  3. ГОСТ Р 58058-2018 «Устойчивость энергосистем. Нормы и требования» - Введ. 01.01.2019 г.
  4. Бацева Н.Л., Фоос Ю.А. Повышение точности расчета объемов управляющих воздействий в централизованной системе противоаварийной автоматики при оценивании состояния энергосистем // Вестник Чувашского университета. 2021. № 3. С. 5-20. doi: 10.47026/1810-1909-2021-3-5-20
  5. Сенюк М.Д., Дмитриева А.А. Апробация алгоритма анализа динамической устойчивости и противоаварийного управления режимом синхронного генератора на многомашинной модели энергосистемы // Электротехнические системы и комплексы. 2022. № 1(54). С. 46-53. doi: 10.18503/2311-8318-2022-1 (54)-46-53
  6. Развитие алгоритма автоматической разгрузки энергоблока при близких коротких замыканиях на основе синхронизированных векторных измерений / А.С. Бердин, А.А. Лисицын, А.Н. Мойсейченков, М.Д. Сенюк // Известия НТЦ единой энергетической системы. 2021. №2(85). С. 76-89.
  7. Воропай Н.И., Электромеханические переходные процессы в электроэнергетических системах: учеб. пособие / Н.И. Воропай. – Благовещенск: Изд-во АмГУ, 2013. – 151 с.
  8. Hierarchical Convolutional Neural Networks for Event Classification on PMU Measurements / M. Pavlovski, M. Alqu-dah, T. Dokic, A.A. Hai, M. Kezunovic, Z. Obradovic // IEEE Transactions on Instrumentation and Measurement. 2021. Vol. 70. 2514813. doi: 10.1109/TIM.2021.3115583
  9. Оценка динамической устойчивости энергосистем на основе метода площадей: научная статья/ Лизалек Н.Н., Ладнова А.Н., Тонышев В.Ф., Попова Е.Ю., Вторушин А.С. – Новосибирск – СибНИИЭ ИАЭС, НГАВТ, 2013. – 14 с. – Текст: электронный // Электронно-библиотечная система eLIBRARY : [сайт]. – URL: https://elibrary.ru/item.asp?id=18879238 (дата обращения 17.07.2022). – Режим доступа: для авториз. пользователей.
  10. Чусовитин П.В., Паздерин А.В. Мониторинг устойчивости энергосистемы на основе динамического эквивалента, определенного по векторным измерениям // Электричество. 2013. № 2. С. 2-10.