
1.1 Этапы разработки фаззи - проекта
Список используемой литературы
В последнее время фаззи-технология завоевывает все больше сторонников из числа разработчиков систем управления. Взяв старт в 1965 году из работ профессора Лотфи Заде, за прошедшие годы фаззи-логика стремительно прошла путь от почти антинаучной теории, практически отвергнутой в Европе и США, до банальной ситуации конца восьмидесятых годов, когда в Японии в широком ассортименте появились фаззи-бритвы, пылесосы, фотокамеры. Сам термин фаззи настолько прочно вошел в жизнь, что на многих языках он просто не переводится. Тем не менее, столь масштабный скачек в развитии фаззи-систем совсем не случаен. Простота и дешевизна разработки фаззи-систем управления заставляет проектировщиков все чаще прибегать к этой технологии
Фаззи-логика - это технология разработки систем управления, которая базируется в основном на интуиции эксперта (оператора) и опыте инженера. Она использует элементы повседневного языка для описания поведения системы в отличие от сложного математического описания при проектировании обычных систем на основе моделей, что позволяет использовать ее для построения устойчивых систем управления для очень сложных объектов.
Фаззи-логику лучше использовать в следующих случаях:
• когда трудно или невозможно построить адекватную математическую модель для поставленной задачи;
• если присутствует большое количество параметров, в том числе и нелинейных или зависящих от времени.
Необходимо помнить, что фаззи-логика не панацея от всех болезней. Общеизвестно, что классические методы управления хорошо работают при полностью детерминированном объекте управления и детерминированной среде. Для систем с неполной информацией или высокой сложностью объекта управления наиболее удачно применение фаззи-логики. Разработка системы на основе фаззи-логики сводится к работе с экспертом- технологом в предлагаемой области[1]. Если имеется практический опыт о характере процесса и взаимодействии всех существенных параметров, то фаззи-логика вносит новые функциональные возможности в существующий процесс разработки. При этом значительно сокращается цикл разработки всей системы при использовании передовых средств поддержки разработки. Разработка систем с фаззи-логикой управления состоит из четырех шагов:
1. Формализация поставленной задачи: определение переменных, сопоставление словесного описания с конкретными физическими значениями.
2. Разработка базы правил, определяющей стратегию управления ввод фаззи-правил и задание метода дефаззификации выходных данных.
3. Оптимизация разработанной системы в режиме интерактивного анализа поведения системы с использованием заранее подготовленных данных или при помощи программной модели объекта управления.
4. Оптимизация в режиме реального времени с подключением созданной системы управления к реальному объекту и оптимизация различных компонентов системы в реальных условиях.
Классическая логика развивается с древнейших времен. Ее основоположником считается еще Аристотель. Логика известна нам как наиболее теоретическая и точная наука.
Вместе с тем классическая или Булева логика имеет один, но очень существенный недостаток, - с ее помощью невозможно описать ассоциативное мышление человека[2].
Классическая логика оперирует только с двумя понятиями "Истина" и "Ложь", исключая любые промежуточные значения.
Решить эту проблему и призвана фаззи-логика. С термином "лингвистическая переменная" можно связать любую физическую величину, для которой необходимо иметь больше значений чем только. "Да" и "Нет". В этом случае определяется необходимое число характеристик и каждой из них ставится в соответствие некоторое конкретное значение, описываемой физической величины.
Функция принадлежности указывает степень принадлежности данной физической величины к определенному заранее установленному множество (лингвистической переменной) в рассматриваемом диапазоне. Степени принадлежности объединяются с помощью соответствующего оператора. Наиболее часто в задачах регулирования с фаззи-логикой для обработки лингвистических переменных используются операторы И и ИЛИ.
Жесткая связь с использованием операторов И и ИЛИ в некоторых случаях может дать недостаточно точные результаты. Более гибкую операцию можно получить допуская некоторую компенсацию одной величины (лингвистической переменной) другой. Этого можно достичь применением ГАММА-оператора.Он показывает в какой степени производится компенсация. При ?=1 операция GAMMA вырождается в операцию И. а при ?=0 - в операцию ИЛИ.
1.1 Этапы разработки фаззи - проекта
При проектировании систем управления, построенных на основе теории фаззи- логики, разрабатывают так называемый фаззи-проект, структурная схема которого приведена на рисунке. Потоки данных на этом рисунке показывают, что фаззификация и дефаззификация связаны непосредственно с пользователем. От фаззификации информация проходит через логическую обработку к дефаззификации[3].
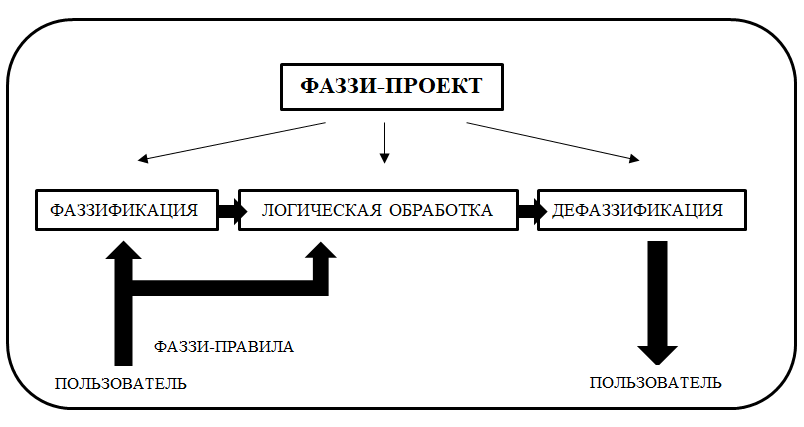
Рисунок 1 - Структура фаззи-проекта
Основные задачи фаззификации:
• проверить нечеткие диапазоны на допустимость;
• отобразить входные четкие данные (измеряемые величины) в виде нечетких диапазонов;
• предоставить результат для логической обработки.
Согласно рисунку данные для логической обработки поступают от фаззификации в виде уже оговоренных нечетких диапазонов.
В правилах заключены знания эксперта о том, что нужно делать, если стало справедливо одно из указанных в фаззификации свойств.
Задачи логической обработки:
• считать входные данные;
• считать правила;
• обработать части правил "ЕСЛИ";
• объединив результаты посредством операторов, получить промежуточные результаты;
• промежуточные результаты с помощью операторов преобразовать в активность нечетких выходов;
• предоставить результат для дефаззификации.
Задачи дефаззификации:
• нечёткие данные (фаззи-данные) преобразовать в четкое значение;
• результат предоставить в распоряжение пользователю.
Входными данными для дефаззификации являются нечеткие данные, поступающие от логической обработки. При дефаззификации решаются задачи, обратные задачам фаззификации. Однако проверка диапазонов здесь не требуется, т.к. влияние извне отсутствует, а логическая обработка дает заведомо правильные данные. Имея нечеткие диапазоны необходимо получить понятный для компьютера и пользователя четкий результат.
Фаззификация служит для того, чтобы представить нечёткую характеристику чёткого состояния переменной в понятной для компьютера форме. Рассмотрим как значение некоторой измеряемой переменной (фаззи-переменной) описать с помощью нечетких диапазонов. Диапазоны в фаззи-логике обозначаются как терм или фаззи- множество. Изображаются они посредством треугольников, трапеций или других кривых - это функция принадлежности или форма терма[4]. Коэффициент оценки называется степень принадлежности и принимает значения от 0.0 до 1.0.
Стопроцентная принадлежность обозначается как 1.0, пятидесятипроцентная - как 0.5 и т. д. Если термы пересекаются, то одному значению входной переменной соответствует несколько степеней принадлежности. Они образуют множество степеней принадлежности. Для обеспечения однозначной фазификации состояния фази-переменной, всегда нужно стараться делать пересечения соседних термов и исключать зазоры между ними. По этой причине первый и последний фаззи-термы чаще всего выбирают в форме трапеций.
Таким образом, фаззи-объект характеризуют:
• имя фаззи-переменной;
• область определения фази-переменной;
• термы;
• границы термов;
• множество степеней принадлежности;
• форма термов.
Результатом фаззификации входной фаззи-переменной является список принадлежностей, который как список входных параметров передается блоку логической обработки. Логическая обработка активизирует в соответствии с заданными фаззи- правилами термы выходной фаззи-переменной. При этом входных и выходных фаззи- переменных может быть несколько[5].
Алгоритм работы фаззи-систем можно разделить на три части: фаззификацию, логическую обработку правил и дефаззификацию Задачей дефаззификации является обратное преобразование лингвистических терминов в физические значения[6].
Существует несколько методов дефазификации:
• Минимум метод
B качестве выходного значения принимается значение лингвистической переменной.
• Максимум метод
B качестве выходного значения принимается значение наибольшей лингвистической переменной.
• Гравитационный метод
Вычисляется центр тяжести площади функции принадлежности выходной величины, образованной всеми лингвистическими переменными.
• Метод высот
Представляет собой упрощенный гравитационный метод и, сокращая время вычислений, дает незначительные отклонения от гравитационного метода.
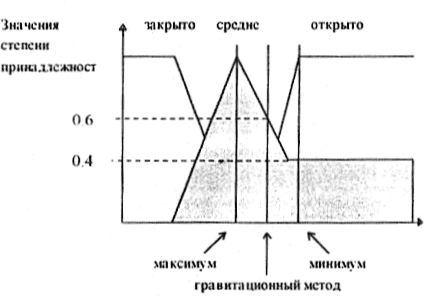
Рисунок 2 - Методы дефаззификации
В технике автоматизации целесообразно использовать те методы фазификации, которые обладают наибольшим быстродействием и требуют наименьших затрат памяти. Выбор того или иного метода определяется как особенностью решаемой задачи, так и опытом проектировщика. В заключении следует отметить, что в "фаззи" как методе обработки нечеткой информации изначально заложен тот факт, что форма функций принадлежности важна только для входных переменных. Для выходных переменных она имеет второстепенное значение. Нечеткость заключается в исходных данных, а результат, определяемый на их основе посредством их оценки или, иначе говоря, взвешиванием, является однозначным[7].
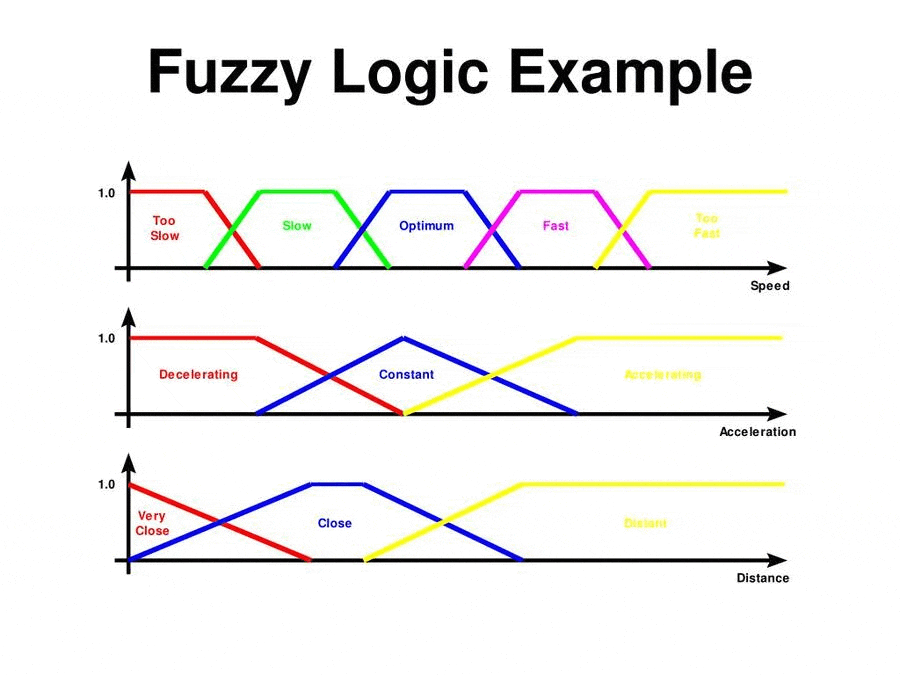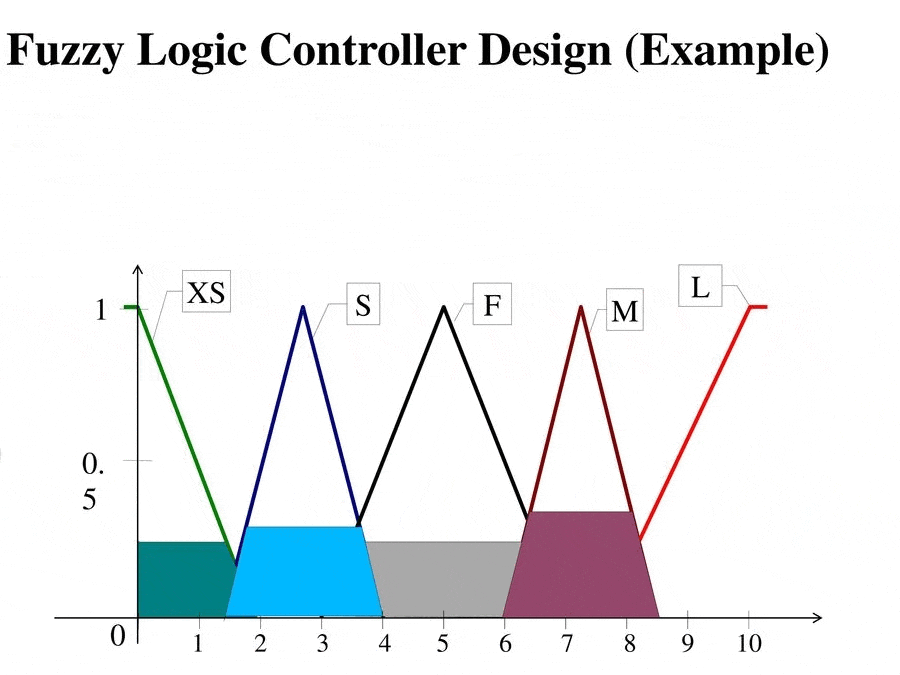
Рисунок 3 - Анимация входных и выходных сигналов в фази логике
Список используемой литературы:
1. Волосенку, С. Вводная глава: Основные свойства нечетких отношений в нечеткой логике; IntechOpen: Лондон, Великобритания, 2020; стр. 3-10.
2. Пегат, А. Нечёткое моделирование и управление / А. Пегат. - М.: БИНОМ. Лаборатория знаний, 2013. - 800 с
3. Fuzzy logic with engineering applications / Timothy J. Ross - John Wiley & Sons, Ltd., 2004. - 628 p.
4. Мерабет, А. Усовершенствованное управление электроприводами: текущие проблемы и перспективы на будущее. Электроника 2020.
5. Штиль В.Я.; Варга Т.; Беншич Т.; Барукчич М. Обзор нечетких алгоритмов, используемых в управлении многодвигательными системами. Электроника 2020
6. Вишневский, В. И. Адаптивный скользящий нечёткий режим управления скоростью асинхронного электродвигателя / В. И.
7. Ли, Л.; Сан, Ю. Адаптивное нечеткое управление для нелинейных неопределенных систем дробного порядка с неизвестными неопределенностями и внешними возмущениями. Энтропия 2015