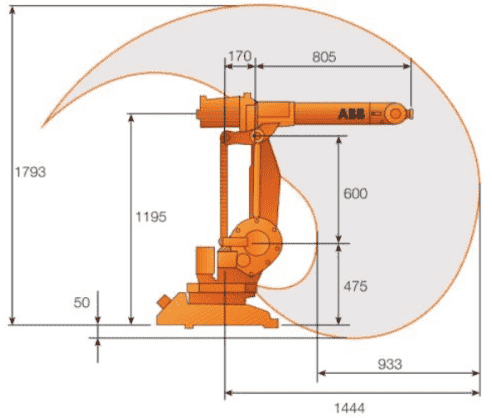
Рисунок 1. Габаритные размеры робота IRB 1410
Авторы: W. Shen, H. Cheng
Автор перевода: К.В. Власов
Источник:2019 International Conference on Intelligent Computing, Automation and Systems (ICICAS)
— pp. 910–912
Wei Shen, Hongjia Cheng Кинематический анализ и моделирование робота ABB на основе MATLAB.
Для того чтобы улучшить точность управления манипулятором, в качестве примера был взят робот ABB IRB 1410, для анализа используются D-H представление, получены решения прямой и обратной задач кинематики с помощью MATLAB. Рабочее пространство робота вычисляется с помощью программного обеспечения MATLAB, а траектория планируется.
Робот IRB 1410, разработанный компанией ABB, представляет собой робота с шестью степенями свободы, все из которых являются поворотными шарнирами, как показано на рисунок 1. грузоподъемность схвата составляет 5 кг; предплечье обеспечивает дополнительную грузоподъемность в 18 кг, которая может быть использована для закрепления различного технологического оборудования. IRB 1410 имеет большой рабочий диапазон, компактную конструкцию и очень компактный схват[1]. Даже в местах с неблагоприятными условиями и многими ограничениями все равно может добиться высокой производительности. Его внешний вид и рабочий диапазон показаны на рисунке 1.

Рисунок 1. Габаритные размеры робота IRB 1410
Разработка D–H модели робота
Чтобы изучить кинематику робота, начальное положение должно быть определено, а системы координат каждого сочленения робота IRB 1410 должны быть установлены так, как показано на рисунке 2. Принцип установки D–H системы следующий: за основу принимается пересечение n и n+1 осей. Zn совпадает с n+1 звеном в любом направлении; ось Xn направлена от оси n к перпендикуляру n+1 оси; ось Yn устанавливается в соответствие с правосторонней системе координат. В соответствие с установленными системами координат и параметры D–H представления высчитываются как это показано в таблице 1. Согласно этой таблице выводятся правила прямой задачи кинематики. Среди них угол поворота Θn звена — это угол, на который нужно повернуть Zn-1 ось, чтобы сделать ось Xn-1 параллельной оси Xn; смещение Dn звена — это такой сдвиг звена вдоль оси Zn-1, чтобы оси Xn-1 и Xn совпадали; длина An — это сдвиг оси Xn таким образом, чтобы начала координат двух систем совпадали; угол α — это угол, на который нужно повернуть звено вокруг оси Xn, чтобы системы координат Zn-1 и Zn стали сонаправленными[2].
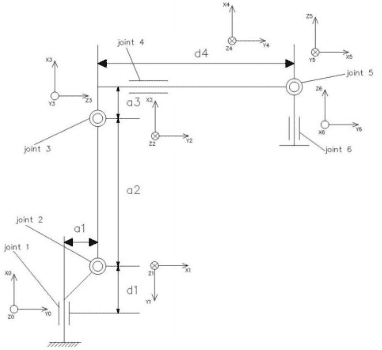
Рисунок2. Системы координат роботаIRB 1410
Таблица 1 — Параметры D–H представления
| Сочленение n | Θ/° | d/мм | a/мм | α/° | Диапазон движения/° |
| 1 | 90 | 475 | 170 | -90 | -170..170 |
| 2 | 90 | 0 | 600 | 0 | -70..65 |
| 3 | 0 | 0 | 120 | -90 | -65..70 |
| 4 | 0 | 805 | 0 | 90 | -150..150 |
| 5 | -90 | 0 | 0 | 90 | -115..115 |
| 6 | 90 | 0 | 0 | 0 | -300..300 |
Анализ прямой кинематики
IRB 1410 — это промышленный робот с шестью степенями свободы. Его кинематика может быть решена с помощью преобразования координат между шестью звеньями и умножения полученных матриц. Матрица преобразования An может быть получена из параметров D–H представления (таблица 1). Эта матрица выглядит следующим образом:
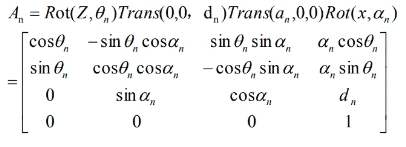
Умножая матрицы от A1 до A6 конечное положение манипулятора определяется выражением: T6=A1A2A3A4A5A6. Так как результат конечной матрицы слишком сложен, он не показан тут[3]. Программа в Matlab, позволяющая получить данную матрицу представлена ниже.
Анализ обратной кинематики
Обратная задача кинематики состоит в том, чтобы зная положение рабочего органа манипулятора в пространстве, узнать значения углов поворота для каждого сочленения. Процесс расчета достаточно сложен [4]. Для решения был использован программный пакет Matlab. Программа, позволяющая находить решение обратной задачи кинематики представлена ниже.
Кинематический анализ робота IRB 1410
В процессе движения необходимо знать положение, скорость и ускорения каждого звена. Для построения конструкции манипулятора использовался Matlab. Программа для создания конструкции в расширении Robotics Toolbox
представлена ниже.
Благодаря написанной программе можно определить как начальное, так и конечное положение манипулятора.
Программа выше иллюстрирует зависимость положения, скорости и ускорения третьего сочленения от времени. Графики показаны на рисунке 3.
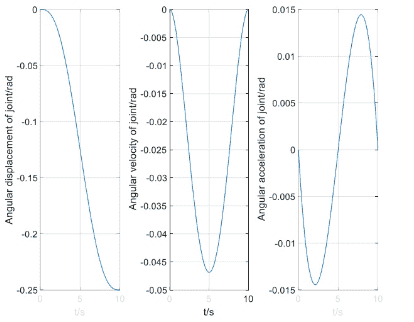
Рисунок 3. Полученные графики
Рабочая область манипулятора определяется набором точек, до которых может достать рабочий орган. В данной статье использовалось расширение Robotics Toolbox
пакета Matlab, чтобы наглядно показать рабочую область манипулятора.
Результат выполнения программы показан на рисунке 4.
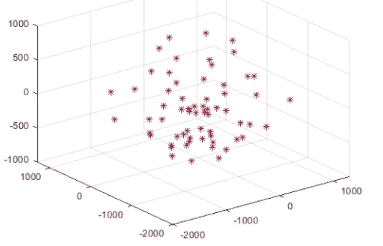
Рисунок 4. Рабочая область манипулятора
В данной статье были найдены параметры D–H представления для промышленного манипулятора IRB 1410 фирмы ABB. Были решены прямая и обратная задачи кинематики с помощью программного пакета Matlab. Проведен детальный анализ кинематики робота. Получены графики положения, скорости и перемещения для одного из звеньев.
1. Choset. Principles of Robot Motion: Theory, Algorithms, and Implementations[J]. Proceedings of the Society for Experimental Biology & Medicine Society for Experimental Biology & Medicine, 2005, 147(1):512–512.
2. P.P.L. Regtien. Sensor systems for robot control[J]. Sensors and Actuators, 17(1-2):91–101.
3. Sabatier, F, De Vivo, A, Vialle, S. [IEEE Comput. Soc Thirteenth IEEE International Workshops on Enabling Technologies: Infrastructure for Collaborative Enterprises — Modena, Italy (14-16 June 2004)] 13th IEEE International Workshops on Enabling Technologies: Infrastructure for Collaborative[J]. :358–363.
4. Apoorva, Deepak, Kapadia, et al. A New Approach to Extensible Continuum Robot Control Using the Sliding-Mode[J]. Computer technology and application: English, 2011(4):293–300.
5. J. A. Becerra, F. Bellas, J. Santos, et al. Complex Behaviours Through Modulation in Autonomous Robot Control[J]. 2005, 3512:449–472.
6. Zhang, Haijie, Zhao, Jianguo. Bio-inspired vision based robot control using featureless estimations of time-to-contact[J]. Bioinspiration & Biomimetics, 12(2):025001.
7. Sampei, M, Furuta, K. Robot control in the neighborhood of singular points[J]. IEEE Journal of Robotics and Automation, 4(3):303–309.