Аннотация
Прокопенко Е.В., Букша Д.Р. Применение платформы DEDUCTOR STUDIO для обработки и восстановления результатов измерения данных. Рассмотрены возможности анализа данных, которые не соответствуют определенным критериям качества. Предварительная обработка таких данных становится необходимым шагом для обеспечения удовлетворительного результата анализа. Необходимость в предварительной обработке возникает независимо от того, какие алгоритмы и технологии используются. В данной статье для обработки таких данных применяется платформа DEDUCTOR STUDIO.
Общая постановка проблемы
Если анализируемые данные не соответствуют определенным критериям качества, то их предварительная обработка становится необходимым шагом для обеспечения удовлетворительного результата анализа. Необходимость в предварительной обработке возникает независимо от того, какие алгоритмы и технологии используются. Также эта задача может представлять самостоятельную ценность в областях, не имеющих непосредственное отношение к анализу данных. Очевидно, что исходные данные чаще всего нуждаются в очистке [1].
В процессе парциальной обработки восстанавливаются пропущенные данные, редактируются аномальные значения, проводится спектральная обработка. В Deductor Studio при этом используются алгоритмы, в которых каждое поле анализируемого набора обрабатывается независимо от остальных полей, то есть данные обрабатываются по частям. По этой причине такая предобработка получила название парциальной. В числе процедур предобработки данных, реализованных в Deductor Studio, входят сглаживание, удаление шумов, редактирование аномальных значений, заполнение пропусков в рядах данных [2].
Постановка задачи
Рассмотрим применение парциальной обработки данных на примере восстановления массива значений измерений, полученных при построении функции Y=Cos(x) на отрезке от 0 до 3,14. Шаг изменения аргумента х – 0,1.
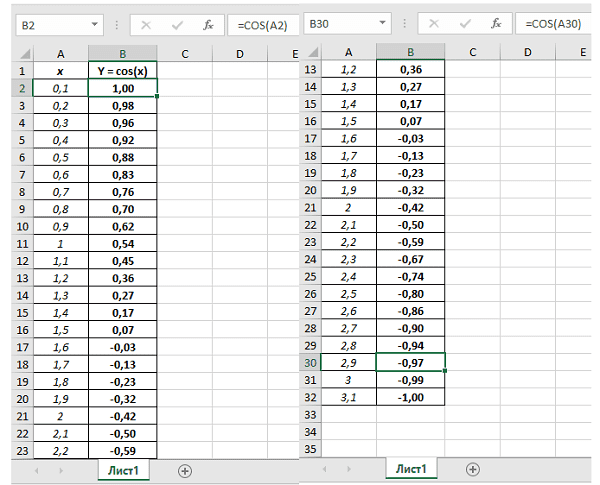
Рисунок 1 - Фрагмент листа Excel с исходными данными
В исходном файле данных удалили 5 - 6 значений функции Y. Например, для х= 0,4; 0,7; 1,3; 2,0; 2,4; 3,0. Полученные изменные данные вставили в область блокнота в виде таблицы.
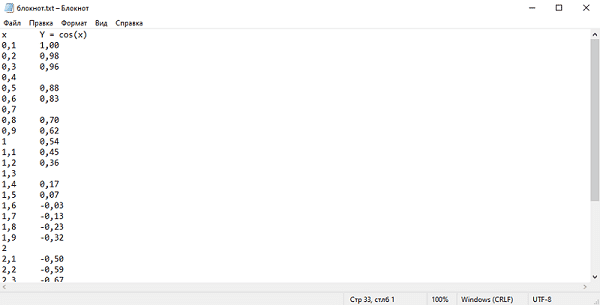
Рисунок 2 - Фрагмент области блокнота с пропущенными данными
Используя платформу Deductor studio с помощью Мастера импорта импортируем данный файл. После импорта файла с пропущенными данными и построением диаграммы для данного файла получаем результаты, представленные на рисунках 3 и 4.
Для восстановления данных используем так называемую спектральную обработку данных, которая находится в мастере обработки платформы Deductor studio. Фрагмент данного окна показан на рисунке 5.
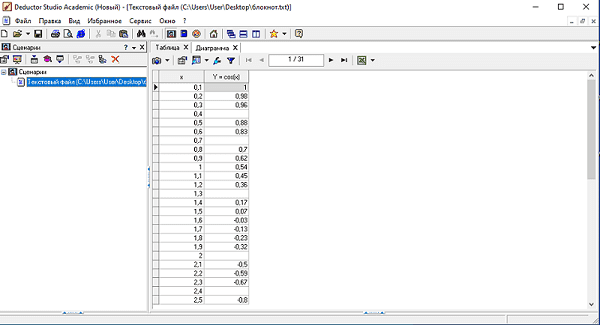
Рисунок 3 - Фрагмент области платформы Deductor studio с пропущенными данными
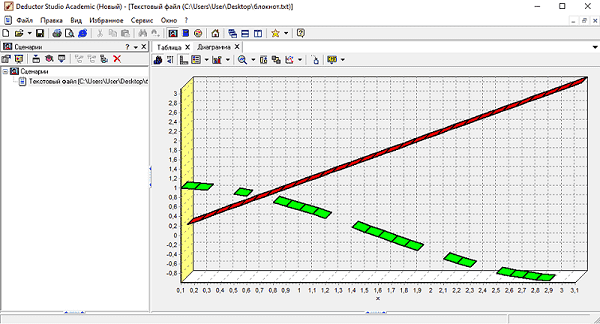
Рисунок 4 - Фрагмент области построения диаграммы Deductor studio с пропущенными данными
Вейвлет-коэффициенты определяются интегральным преобразованием сигнала. Полученные вейвлет-спектрограммы дают четкую привязку спектра различных особенностей сигналов ко времени. Вейвлет-преобразование (англ. Wavelet transform) — интегральное преобразование, которое представляет собой свертку вейвлет-функции с сигналом.
Cпособ преобразования функции (или сигнала) в форму, которая или делает некоторые величины исходного сигнала более поддающимися изучению или позволяет сжать исходный набор данных. Вейвлетное преобразование сигналов является обобщением спектрального анализа.После обработки спектральным анализом полностью восстанавливаются исходные данные и перестраивается диаграмма построения данных.
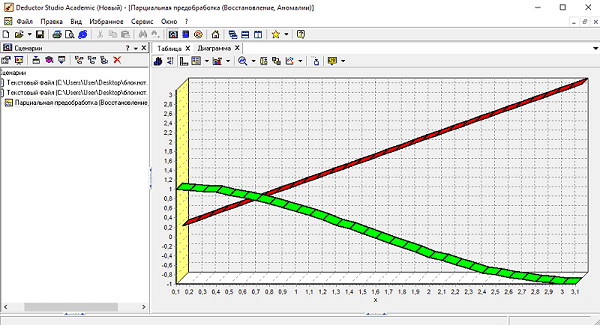
Рисунок 5 - Фрагмент области построения диаграммы Deductor studio с восстановленными данными
Вывод
В данной статье рассмотрен один из способов восстановления пропущенных данных, а именно парциальная обработка данных. Данный способ используется при большом объеме данных и является наиболее эффективным не только в математике, но и в других областях знаний.
Список использованной литературы
1. Курносов М.Г. Анализ и организация функционирования вычислительных систем / Курносов М.Г., Берлизов Д.М.. — Новосибирск : Автограф, 2020. — 54 c. [Электронный ресурс]. — Режим доступа: https://www.iprbookshop.ru/102116.html/ – Загл. с экрана.
2. Александровская Ю.П. Многомерный статистический анализ в экономике : учебное пособие / Александровская Ю.П. — Казань : Казанский национальный исследовательский технологический университет, 2017. — 96 c. [Электронный ресурс]. — Режим доступа:
https://www.iprbookshop.ru/79330.html – Загл. с экрана.