Аннотация
C. В. Зыкин. Представление результатов анализа данных в многомерном пространстве параметров. При анализе данных представление границ между классами объектов в большинстве случаев считается второстепенной проблемой. Однако последующее использование результатов анализа (например, в диагностических задачах или при приобретении необходимых свойств объекта путем контроля параметров) должно основываться на определении границ и точности их описания. Это подчеркивает необходимость разработки и использования универсальных методов представления результатов анализа данных. В данной статье рассматривается модель данных для прикладной поддержки принятия решений системы, в которых одним из компонентов являются графические данные, т.е. области в многомерном пространстве, ограниченные общими поверхностями. Предложена математическая модель, которая достаточно строго очерчивает диапазон возможных графических приложений. В статье предлагается содержательный подход к описанию ошибки определения границ. Рассмотренный материал может послужить основой для технологии хранения и использования результатов анализа данных.
1. Введение
В настоящее время методы анализа данных широко используются для выявления закономерностей в пространстве параметров исследуемых объектов. В результате анализа объекты могут быть распределены по множеству различных классов. В методах кластерного анализа чаще всего используются области круглой формы , а диагностика выполняется по расстоянию от центроидов. При наличии взаимных нелинейных зависимостей параметров этот подход становится неуместным, поскольку центроид может находиться за границами соответствующей области пространства параметров. При дискриминантном анализе предполагаются более точно определенные границы предметной области. В этом случае для аппроксимации нелинейных зависимостей используются кусочно-линейные функции, что значительно усложняет подготовку исходных данных из-за определения связности в многомерном пространстве. Это также вносит дополнительную ошибку в определение границ.
Использование результатов анализа данных лежит в основе информационной поддержки процесса принятия решений. Такая информация должна быть подвергнута проверке и утверждению перед использованием. Однако в такой ситуации сложность анализа данных удваивается, и он не всегда выполняется квалифицированным образом. Выходом из этой ситуации является организация хранения информации, прошедшей квалифицированную экспертизу, в унифицированном виде в базе данных.
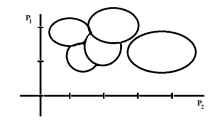
Рисунок 1 - Пример разграничения кластеров
Такое представление результатов анализа данных соответствует графическому представлению областей в пространстве параметров. Каждая область соответствует одному классу объектов одного типа.
Способ определения границ и их погрешностей зависит от поставленных целей и средств представления исходных данных. Публикация [1] развивает метод Лана и Деметса, которые предложили функцию затрат, аппроксимирующую границу О'Брайена-Флеминга, основанную на процессе броуновского движения. Метод был распространен на семейство с аддитивными границами и условной ошибкой.
В [2] предлагается новый метод оценки неопределенности границ пространственных кластеров , идентифицированных с помощью статистики пространственного сканирования. Для каждого местоположения пространственных данных вычисляется значение принадлежности к истинному кластеру. С помощью имитационного моделирования показано, что этот метод обеспечивает способ определения и визуализации достоверности или неопределенности каждого местоположения. Метод был реализован для статистики кругового пространственного сканирования агрегированных данных.
Процедуры для разделения больших коллекций сильно перемешанных наборов данных разных классов приведены в [3]. В качестве границ кластеров используются гиперсферические или гиперэллипсоидальные кластеры. Инкрементные процедуры генерируют минимальное количество таких кластеров. Однако каждый кластер должен содержать максимальное количество точек данных одного и того же класса. Разработанные процедуры представляют собой расширение алгоритмов и могут быть применены к моделированию границ кластера для решения многочисленных задач анализа данных.
Во многих работах не обсуждается проблема выделения кластеров и погрешности их измерения. Например, особенности кластеризации мониторинга экологических данных обсуждаются в [4]. Предлагается комплексная оценка экологической ситуации, которая помогает выявить структурные связи между показателями мониторинга. Однако в статье используются ”пиксельные” представления кластеров . Одним из недостатков такого представления кластеров является избыточность описания и плохая масштабируемость.
2. Требования к модели данных
Математическое описание границ кластера в пространстве параметров должно удовлетворять следующим требованиям:
- Элемент с размерностью i, i = 1, n, ограничен элементами с размерностью i - 1, i - 2, ..., 0, одновременно принадлежащими исходному элементу и соседним элементам с той же размерностью. Для реализации этого принципа были введены номера элементов , и для каждого элемента с размерностью i - 1 указаны номера элементов с размерностью i, к которым он принадлежит.
- Есть несколько точек, через которые граница должна проходить точно.
- Есть несколько точек, для которых граница проходит в пределах погрешности измерения этих точек.
- Есть несколько точек, для которых граница проходит на максимальном расстоянии.
- Границы должны соответствовать топологическим требованиям области применения. Элементы с размерностью n - 1, n - 2, ..., 1 не должны содержать ложных экстремумов и точек перегиба. Это может быть связано с ошибками в данных или заниженным значением расхождения (ошибки). В первом случае необходимо скорректировать данные. Во втором случае необходимо увеличить расхождение, т.е. сопоставить его с реальной точностью имеющихся данных.
- Соединение элементов (поверхностей), подлежащих аппроксимации по отдельности, выполняется таким образом, чтобы их продолжение принадлежало элементу с большим размером, для которого исходные элементы не являются граничными. Эта проблема обычно возникает в случае отсутствия экспериментальных данных и решается путем добавления новых точек, полученных расчетным методом.
С помощью представления результатов анализа данных могут быть решены различные задачи, например:
- распознавание объекта по набору параметров;
- определение состояния объекта;
- управление переходом объекта в целевое состояние;
- минимизация энергозатрат при управлении объектом и т.д.
Унификация представления результатов анализа данных позволит создать общие информационные ресурсы. Поскольку данные в такой системе структурированы, для их хранения и обработки целесообразно использовать технологии баз данных.
3. Математическая модель представления данных
Растущий интерес к способам представления и обработки графической информации с помощью примитивов наблюдается уже много лет [5,6]. С одной стороны, это вызвано необходимостью создания автоматизированных систем, использующих графическую информацию, с другой стороны, это связано с возросшими техническими возможностями вычислительных средств.
В общем, результаты анализа данных представляют собой n - мерные объекты в пространстве параметров. Способ представления данных должен обеспечивать эффективное хранение и обработку данных.
3.1. Выбор метода представления данных
Существует множество способов графического представления реальных объектов. Как правило, они используются для описания двумерных и трехмерных объектов. На выбор того или иного метода влияют следующие основные факторы:
- геометрические свойства объектов;
- прикладные задачи, решаемые в данной информационной системе.
Под геометрическими свойствами понимается структура (топология) объектов и требуемая точность (адекватность) их описания.
Пиксельное представление объектов [7], используется для обработки различных типов фотоматериалов и позволяет решать практически любые задачи анализа. Однако из-за низкой точности этот метод не используется в областях, где требуется четкое разграничение объектов на графике. Например, его нельзя использовать при автоматизированном проектировании, геодезии и т.д., то есть везде , где требуется масштабирование на больших расстояниях.
Для границ кластера целесообразно использовать аппроксимации функциональных зависимостей. Это связано не только с необходимостью масштабирования, хотя это актуально для диагностики вблизи границ, но и для построения самих границ в дискриминантном анализе. В [8], предлагается использовать функции параметров для представления многомерной графической информации:

Такой метод имеет неоспоримое преимущество, когда нет необходимости в однозначном вычислении функции y = y(x) при расчете некоторых характеристик, например, получении двумерных сечений, проекций, расчете объема и т.д. Однако этих алгоритмов недостаточно при работе с результатами анализа данных. Для дальнейшей обработки информации, полученной путем аппроксимации границ кластера, важно рассчитать функцию y = y(x), поэтому предпочтение отдается однозначным функциям. В этом случае многозначные поверхности разрушаются, разбиваются на однозначные области и аппроксимируются отдельно.
Следует также отметить, что параметрическое представление поверхностей при n > 3 требует введения связности [9] для точек предполагаемых поверхностей, что не гарантирует правильного формирования границ и усложняет подготовку исходных данных.
3.2. Формальное описание модели данных
Результаты анализа данных должны быть представлены доменами в пространстве параметров источника. Домены пространства (кластеры) разделены поверхностями, имеющими на один размер меньше, чем сами области. Поверхности образуют каркас представления данных, ограниченный пространством изменений параметров.
Вывод
Предлагаемая модель данных универсальна с точки зрения описания предметных областей в многомерном евклидовом пространстве. Область ее применения не ограничивается анализом данных. Это могут быть САПР -системы в гражданском строительстве, системы в геологоразведке и т.д. Вопрос вычисления границ области выходит за рамки данной статьи. Наиболее подходящими в данном случае являются методы аппроксимации смешанной поверхности. Однако классические методы аппроксимации должны быть адаптированы к этой задаче (необходимо модифицировать критерий оптимизации), поскольку в пространстве, задаются не точки поверхностей, а точки, от которых поверхности должны быть на значительном расстоянии.
Список использованной литературы
1. Xi D. and Gallo P. 2019. An additive boundary for group sequential designs with connection to conditional error Statistics in Medicine 38. – pp 4656–69.
2. Oliveira L. P., Cancado L. F., de Souza G., Moreira G. P. and Kulldorff M. 2018 Border analysis for spatial
clusters International Journal of Health Geographics 17 5.
3. Kong Q. L. and Zhu Q. M. 2007 Incremental procedures for partitioning highly intermixed multi-class datasets into hyper-spherical and hyper-ellipsoidal clusters Data & Knowledge Engineering 63. – pp 457–477.
4. Kashirina I. L., Fedutinov K. A., Azarnova T. V. and Bondarenko Iu. V. 2019 System analysis of monitoring
ecological information using Fuzzy ART neural network Journal of Physics: Conference Series 1203 012090.
5. Newman W. M. and Sproull R. F. 1973 Principles of interactive computer graphics (New York : McGraw-Hill).
– p 570.
6. Kaiser A., Zepeda A. Y. and Boubekeur T. 2019 A survey of simple geometric primitives detection methods
for captured 3D data Computer Graphics Forum 38. – pp 167–196.
7. Li D, Yang D. Y. and Liu G. B. 2019 Research on Key Technologies of Night Detection of License Plate
Recognition System 2nd International Conference on Mechanical, Electronic and Engineering Technology
(MEET-2019).– pp 101–105.
8. Geist M. and Pietquin O. 2011 Parametric value function approximation: A unified view IEEE Symposium on
Adaptive Dynamic Programming and Reinforcement Learning (ADPRL) 11-15 April 2011. – pp 9–16.
9. Fusch P., Fusch G. E. and Ness L. R. – 2018 Denzin’s Paradigm Shift: Revisiting Triangulation in Qualitative Research Journal of Social Change 10. – pp 19–32.