Abstract on the topic of the work
Content
- Introduction
- Purpose and research objectives
- Relevance of the study
- The object and subject of the study
- Abstract
- Conclusion
- List of used literature
Introduction
Currently, research in the field of vibrations and vibrations is of great importance in various technical and engineering fields. They allow you to better understand and optimize the behavior of the system, as well as develop effective methods for monitoring and controlling fluctuations. One of the important aspects of the study of system oscillations is the study of related spatial oscillations [1].
Systems of bodies with a third-order axis of symmetry are particularly interesting for research, since they have a complex structure and dynamics [2]. These systems can be represented as connected solids with a certain number of degrees of freedom [3].
However, the analysis of the study of related spatial vibrations of a system of bodies of the third order is a difficult task requiring the use of special modeling methods. Computer technologies and software are widely used for this purpose [4].
PC modeling allows for more accurate and precise numerical calculations, as well as stimulating and visualizing the behavior of the system. Using a PC, you can create a mathematical model of the system, taking into account all its features and parameters. Then numerical calculations and analysis of the results are carried out, which allows a deeper understanding of the dynamics of the system.
In this paper, we will consider the study of related spatial vibrations of a system of bodies with a third-order axis of symmetry and their modeling on a PC. More specifically, we will present modeling and numerical analysis algorithms, as well as examples of research results. This will provide a more complete understanding of the behavior of the system and its dynamics, which in turn can be useful for optimizing and managing such systems.
Purpose and research objectives
Purpose: The purpose of this topic is to develop a computer model of the associated spatial vibrations of a system of bodies with a third-order axis of symmetry.
Research: The research objective is related to the study of methods of dynamics of systems with a large number of degrees of freedom, mathematical models consisting of a system of differential equations that describe the motion of each body in space.
Relevance of the study
The study of related spatial vibrations of a system of bodies is an important task in the field of system dynamics. It can be applied in various fields such as mechanics, physics, engineering and astronomy.
Related spatial vibrations of the third order arise in systems consisting of three bodies connected to each other as a result of the interaction of forces. These can be, for example, mechanical systems consisting of three masses connected by springs or other elements, or systems that simulate the behavior of astronomical objects such as triple stars or satellites.
The study of related spatial oscillations of the third order requires the use of methods of dynamics of systems with a large number of degrees of freedom. Mathematical models consisting of a system of differential equations that describe the motion of each body in space are used to describe such vibrations.
The analysis of related spatial vibrations of the third order makes it possible to understand the interaction between bodies in the system, to identify the characteristics of oscillatory motion, such as natural frequencies, modes of oscillation, forms of oscillatory movements and their influence on the overall behavior of the system.
The study of related spatial vibrations of a system of bodies is of great importance for the development of new designs, optimization of mechanisms, forecasting the behavior of astronomical objects and other applied tasks. Therefore, this topic is an urgent and in-demand scientific field that attracts the attention of researchers from all over the world.
The object and subject of the study
The object of research is a model of coupled spatial vibrations of a system of bodies with a third-order axis of symmetry, which can be created using various methods and software. This model includes various parameters in the form of variables that have their own values.
The subject of the study is the process of modeling the associated spatial vibrations of a system of bodies with a third–order axis of symmetry, which includes the study of mathematical models, calculations and analysis of the results obtained.
The object and the subject of modeling research are related to each other, since the subject of research is part of the object of research. Modeling makes it possible to study and analyze the oscillatory process more effectively and predict its operation under different conditions, with different input data.
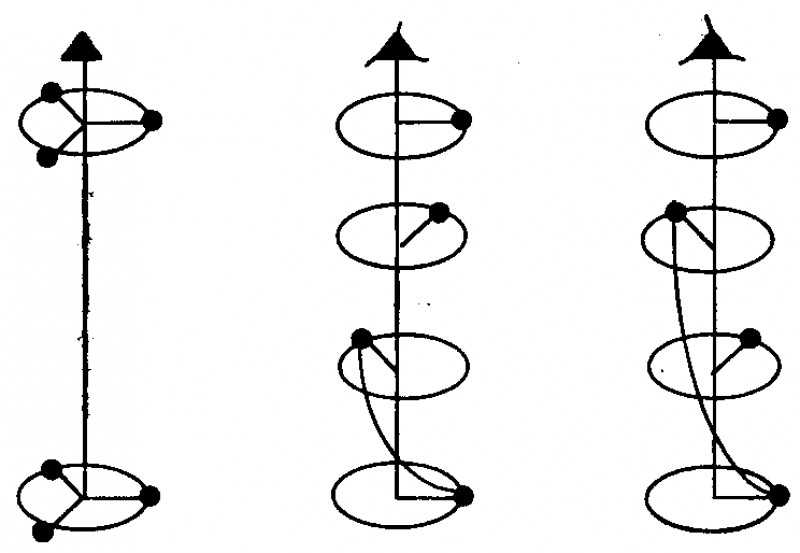
Figure 1 - Vibrations of bodies
Abstract
The study of related spatial vibrations of a system of bodies with a third-order axis of symmetry and their modeling on a personal computer (PC) is an urgent topic from the field of physics and mathematics. In this abstract, we will consider the main aspects of this study.
Systems of bodies with a third-order symmetry axis include objects that have three-way or three-axis symmetry, such as regular polyhedra, molecules, atoms, and other structures. Studying the vibrations of such systems is important for understanding their properties, stability and dynamics [6].
The mathematical modeling method is used to study the related spatial oscillations of such systems. PC modeling allows you to analyze various system parameters, perform numerical calculations and obtain results that can be used for further analysis and understanding of the system [7].
One of the main tools for modeling such systems on a PC is numerical methods. Numerical methods make it possible to approximate differential equations that describe the oscillations of a system and solve them using iterative algorithms. Examples of such methods are finite element methods, finite difference methods, and the finite volume method. [8].

Figure 2 - Oscillation inside the bulb
For successful modeling and investigation of vibrations of a system of bodies with an axis of symmetry of the third order, reliable mathematical models are needed that take into account the features of such systems. An important step is the construction of a mathematical model of the system, which can be based on various approaches such as molecular dynamics, quantum mechanics and others.
After constructing a mathematical model, it is possible to conduct numerical experiments, analyze the results and compare them with experimental data. This allows you to refine the model and get more accurate results.
The study of related spatial vibrations of a system of bodies with a third-order axis of symmetry and their modeling on a PC are an active and important area of research. They have various practical applications, such as the development of new materials, process optimization in the chemical industry, the development of new modeling methods and others.
In conclusion, the study of related spatial vibrations of a system of bodies with a third-order axis of symmetry and their modeling on a PC are important tasks that require the use of mathematical methods and numerical algorithms. This allows us to expand our understanding of the system and gain new knowledge that can be used in various fields of science and technology.
Conclusion
In general, the study of related spatial vibrations of a system of bodies with a third-order axis of symmetry and their modeling on a PC is an urgent and promising task that can lead to the development of new technologies and improve the performance and quality of systems.List of used literature
- Гетманова Е.Г., Костарев Д.Б. Резонансные явления в системе связанных осцилляторов// Электромагнитные волны и электронные системы. 2001. Т. 6. № 5. – Режим доступа: [Ссылка]
- Коткин Г.Л., Сербо В.Г. Сборник задач по классической механике. М.: Наука, 1977. – Режим доступа: [Ссылка]
- Ландау Л.Д., Лифшиц Е.М. Механика. М.: Наука, 2000. – Режим доступа: [Ссылка]
- Крауфорд Ф. Волны. М.: Наука, 1974. – Режим доступа: [Ссылка]
- Федоренко Р. П. Введение в вычислительную физику: учеб. пособие для вузов. М.: Изд–во Моск. физ.–техн. ин–та, 1994. 528 с. – Режим доступа: [Ссылка]
- Тихонов А. Н., Самарский А. А. Уравнения математической физики. М.: Наука, 1966. 724 с. – Режим доступа: [Ссылка]
- Поттер Д. Вычислительные методы в физике. М.: Мир, 1975. 392 с. – Режим доступа: [Ссылка]
- Кунин С. Вычислительная физика. М.: Мир, 1992. 518 с. – Режим доступа: [Ссылка]
- Коткин Г.Л., Сербо В.Г. Сборник задач по классической механике. М.: Наука, 1977. – Режим доступа: [Ссылка]
