English
ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

В настоящее время исследования в области колебаний и вибраций имеют большое значение в различных технических и инженерных областях. Они позволяют более глубоко понять и оптимизировать поведение системы, а также разработать эффективные методы контроля и управления колебаниями. Одним из важных аспектов исследования колебаний системы является изучение связанных пространственных колебаний [1].

Системы тел с осью симметрии третьего порядка являются особенно интересными для исследования, так как они обладают сложной структурой и динамикой [2]. Эти системы могут быть представлены как связанные твёрдые тела, обладающие определенным числом степеней свободы [3].

Однако анализ исследования связанных пространственных колебаний системы тел третьего порядка является сложной задачей, требующей использования специальных методов моделирования. Для этого широко применяются компьютерные технологии и программное обеспечение [4].

Моделирование на ПК позволяет проводить более точные и точные численные расчеты, а также симулировать и визуализировать поведение системы. При помощи ПК можно создавать математическую модель системы, учитывая все ее особенности и параметры. Затем проводятся численные расчеты и анализ результатов, что позволяет более глубоко понять динамику системы.

В данной работе мы рассмотрим исследование связанных пространственных колебаний системы тел с осью симметрии третьего порядка и моделирование их на ПК. Более конкретно, мы представим алгоритмы моделирования и численного анализа, а также примеры результатов исследования. Это позволит получить более полное представление о поведении системы и ее динамике, что в свою очередь может быть полезным для оптимизации и управления такими системами.

Цели и задачи исследования

Цель: Целью данной темы является разработка компьютерной модели связанных пространственных колебаний системы тел с осью симметрии третьего порядка.

Задача: Задача исследования связана с изучением методов динамики систем с большим числом степеней свободы, математических моделей, состоящих из системы дифференциальных уравнений, которые описывают движение каждого тела в пространстве.

Актуальность исследования

Исследование связанных пространственных колебаний системы тел является важной задачей в области динамики систем. Оно может быть применено в различных областях, таких как механика, физика, инженерия и астрономия.

Связанные пространственные колебания третьего порядка возникают в системах, состоящих из трех тел, связанных между собой в результате взаимодействия сил. Это могут быть, например, механические системы, состоящие из трех масс, соединенных пружинами или другими элементами, либо системы, моделирующие поведение астрономических объектов, таких как тройные звезды или спутники.

Изучение связанных пространственных колебаний третьего порядка требует применения методов динамики систем с большим числом степеней свободы. Для описания таких колебаний используются математические модели, состоящие из системы дифференциальных уравнений, которые описывают движение каждого тела в пространстве.

Анализ связанных пространственных колебаний третьего порядка позволяет понять взаимодействие между телами в системе, выявить характеристики колебательного движения, такие как собственные частоты, моды колебаний, формы колебательных движений и их влияние на общее поведение системы.

Исследование связанных пространственных колебаний системы тел имеет большое значение для разработки новых конструкций, оптимизации работы механизмов, прогнозирования поведения астрономических объектов и других прикладных задач. Поэтому данная тема является актуальной и востребованной научной областью, привлекающей внимание исследователей со всего мира.

Объект и предмет исследования

Объект исследование - модель связанных пространственных колебаний системы тел с осью симметрии третьего порядка, которая может быть создана с использованием различных методов и программного обеспечения. Данная модель включает в себя различные параметры в виде переменных, которые имеют свои значения.

Предмет исследования – процесс моделирования связанных пространственных колебаний системы тел с осью симметрии третьего порядка, который включает в себя исследование математических моделей, расчеты и анализ полученных результатов.

Объект и предмет исследования моделирования связаны между собой, так как предмет исследования является частью объекта исследования. Моделирование позволяет более эффективно изучать и анализировать колебательный процесс и предсказывать его работу в различных условиях, с различными вводными данными.

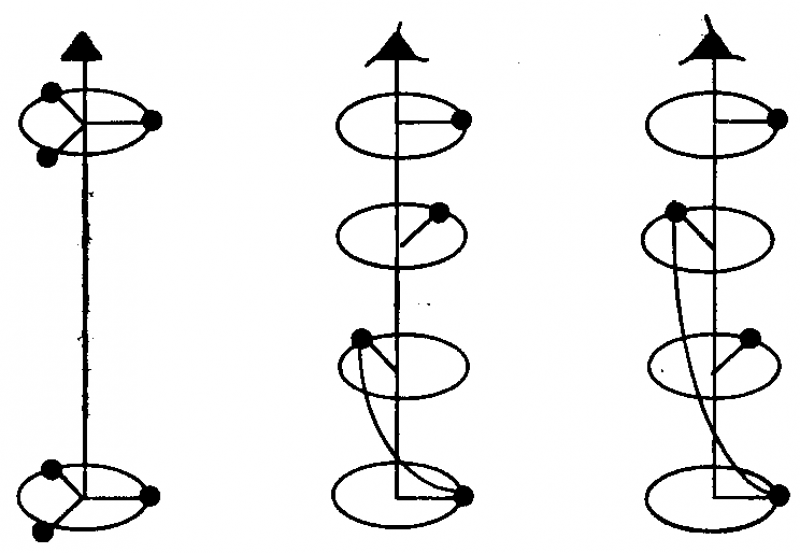
Колебание тел

Рис.1 - Колебания тел

Реферат

Исследование связанных пространственных колебаний системы тел с осью симметрии третьего порядка и их моделирование на персональном компьютере (ПК) представляет собой актуальную тему из области физики и математики. В данном реферате рассмотрим основные аспекты этого исследования.

Системы тел с осью симметрии третьего порядка включают в себя объекты, которые обладают трехсторонней или триосевой симметрией, такие как правильные многогранники, молекулы, атомы и другие структуры. Изучение колебаний таких систем является важным для понимания их свойств, стабильности и динамики [6].

Для исследования связанных пространственных колебаний таких систем применяется метод математического моделирования. Моделирование на ПК позволяет анализировать различные параметры системы, проводить численные расчеты и получать результаты, которые могут быть использованы для дальнейшего анализа и понимания системы [7].

Один из основных инструментов для моделирования таких систем на ПК – это численные методы. Численные методы позволяют аппроксимировать дифференциальные уравнения, которые описывают колебания системы, и решать их при помощи итеративных алгоритмов. Примерами таких методов являются методы конечных элементов, методы конечных разностей и методы конечных объемов [8].

Колебание внутри лампочки

Рис.2 - Колебание внутри лампочки

Для успешного моделирования и исследования колебаний системы тел с осью симметрии третьего порядка необходимы надежные математические модели, которые учитывают особенности таких систем. Важным этапом является построение математической модели системы, которая может быть основана на различных подходах, таких как молекулярная динамика, квантовая механика и другие.

После построения математической модели возможно проведение численных экспериментов, анализ результатов и сравнение с экспериментальными данными. Это позволяет уточнить модель и получить более точные результаты.

Исследование связанных пространственных колебаний системы тел с осью симметрии третьего порядка и их моделирование на ПК являются активной и важной областью исследования. Они имеют различные практические применения, такие как разработка новых материалов, оптимизация процессов в химической промышленности, разработка новых методов моделирования и другие.

В заключение, исследование связанных пространственных колебаний системы тел с осью симметрии третьего порядка и их моделирование на ПК являются важными задачами, которые требуют использования математических методов и численных алгоритмов. Это позволяет расширить наше понимание системы и получить новые знания, которые могут быть использованы в различных областях науки и техники.

Вывод

В целом, исследование связанных пространственных колебаний системы тел с осью симметрии третьего порядка и их моделирование на ПК является актуальной и перспективной задачей, которая может привести к разработке новых технологий и обеспечить улучшение производительности и качества систем.

Список использованной литературы

  1. Гетманова Е.Г., Костарев Д.Б. Резонансные явления в системе связанных осцилляторов// Электромагнитные волны и электронные системы. 2001. Т. 6. № 5. – Режим доступа: [Ссылка]
  2. Коткин Г.Л., Сербо В.Г. Сборник задач по классической механике. М.: Наука, 1977. – Режим доступа: [Ссылка]
  3. Ландау Л.Д., Лифшиц Е.М. Механика. М.: Наука, 2000. – Режим доступа: [Ссылка]
  4. Крауфорд Ф. Волны. М.: Наука, 1974. – Режим доступа: [Ссылка]
  5. Федоренко Р. П. Введение в вычислительную физику: учеб. пособие для вузов. М.: Изд–во Моск. физ.–техн. ин–та, 1994. 528 с. – Режим доступа: [Ссылка]
  6. Тихонов А. Н., Самарский А. А. Уравнения математической физики. М.: Наука, 1966. 724 с. – Режим доступа: [Ссылка]
  7. Поттер Д. Вычислительные методы в физике. М.: Мир, 1975. 392 с. – Режим доступа: [Ссылка]
  8. Кунин С. Вычислительная физика. М.: Мир, 1992. 518 с. – Режим доступа: [Ссылка]