RU DonNTU Masters' portal

Abstract

Table of contents

Introduction

At the moment, the transportation of goods is a fundamental point in any manufacturing company. The correct calculation of the loading of goods is one of the most important stages in the transportation of goods, since the effectiveness of the delivery as a whole will depend on the quality of this stage. There are often cases when, due to incorrect calculation, some of the goods remained unloaded or turned out to be in the wrong part of the body in which they should be. Such errors significantly increase the time and cost of transporting goods. To solve this problem, it is necessary to develop specialized software that will automatically calculate the most effective ways of loading goods and make recommendations to improve the speed and quality of transportation.

1. Description of the problem and its relevance

Delivery of goods (cargo) is one of the key logistical functions associated with the movement of products by vehicle using a certain technology in the supply chain and consisting of logistical operations and functions, including forwarding, cargo handling, packaging, transfer of rights and ownership of cargo, risk insurance, customs procedures, etc.

Road transport, unlike other types, has high maneuverability and mobility, and in many cases is the only possible mode of transport that ensures the delivery of goods directly from the sphere of production to the sphere of consumption without the participation of other modes of transport.

The main disadvantage of road transport is the relatively high cost of transportation, which is usually charged according to the maximum load capacity of the car. Other disadvantages of this type of transport include the low level of mechanization of loading and unloading operations.

To increase the turnover of transport in the sectors of the economy, it is necessary to sharply reduce manual labor and the number of transshipment operations during the movement of goods along the chain: commodity producer – warehouses – retail trade. It is possible to achieve these goals when changing the technology of the transportation process by introducing transport and technological systems into this process [1].

One of the most significant problems encountered in the supply chain is the disruption of loading. Delays in planning the placement of cargo in vehicles can cause not only operational difficulties, but also lead to financial losses, negative environmental consequences and even an increased risk of road accidents.

In modern legislation in the field of cargo transportation, there are strict regulations governing weight restrictions on various types of vehicles. In accordance with the decree of the Government of the Russian Federation dated 12/21/2020 N 2200 [2], the maximum permissible load capacities are set depending on the number of axles, which is aimed at ensuring the safety and stability of vehicles in motion.

However, an important aspect in ensuring the safety and stability of vehicles is not only the observance of maximum load capacities, but also the correct distribution of load on individual axles. This prevents excessive pressure on some axles and insufficient pressure on others, which can significantly affect stability and traffic safety. Figure 1 shows the correct load distribution along the semi-trailer (Fig. 1) [3].

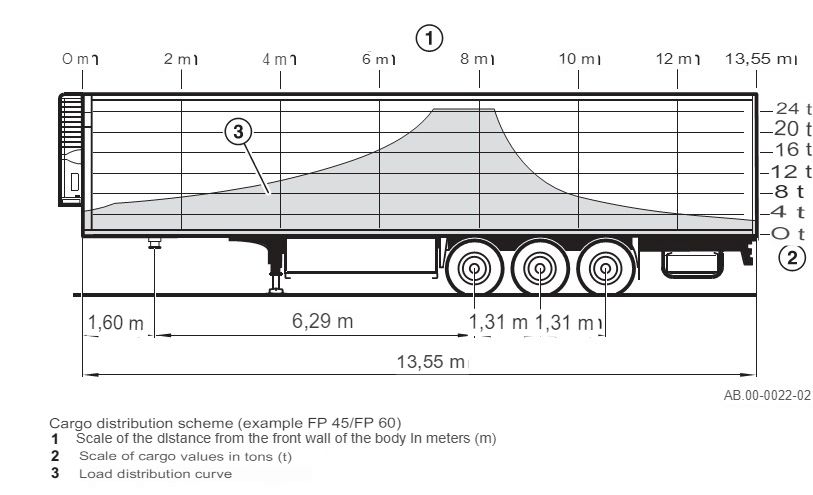
Cargo weight distribution scheme

Figure 1 – Cargo mass distribution diagram [3]

Usually, they are transported on standard pallets in the back of a vehicle. With a homogeneous load, this allows us to consider its mass evenly distributed along the length of the body with the center of gravity in the base of the car and use the schemes shown in Fig. 2 (a, b) to calculate axial loads and permissible payload limits [4]. There are many features that affect the final result of calculations. It is important to get the correct calculations so that the suspension of the car is in good working order, balancing is done, the convergence and camber of the wheels are set up correctly. In principle, do not allow the trailer to deflect under the weight of the load and ensure a flat surface of the cargo platform [5]

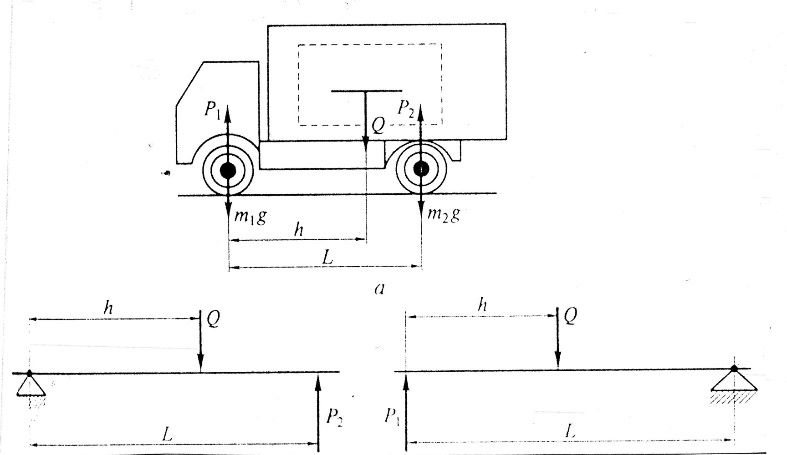
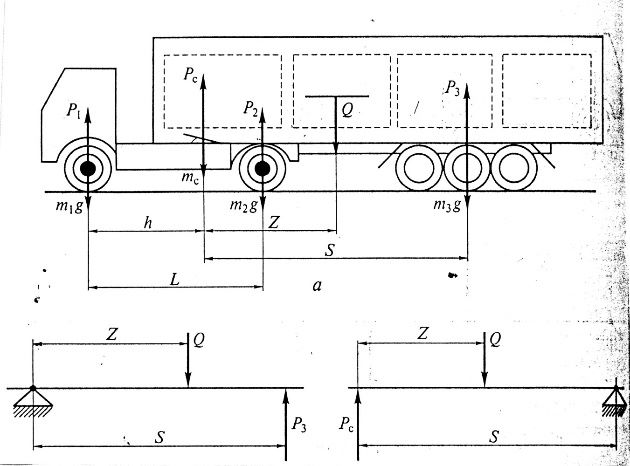
Figure 2 – Diagrams for calculating the permissible weight of the cargo [4]:
a – in the back of a car; b – in the back of a road train

Despite these regulations, the problem of proper distribution of cargo in vehicles remains relevant. Loading semi-trailers with the maximum permissible cargo volumes requires special attention to the distribution of weight in order to prevent uneven pressure on the axles and, consequently, comply with regulations and ensure the safety of transportation.

In this context, solving the problem of optimizing the loading of transport, taking into account the uniform distribution of the load on the axles, acquires not only economic, but also social importance. It is aimed at improving the efficiency of logistics processes, reducing the time of loading and unloading operations and compliance with safety standards, which, in turn, contributes to a more stable and efficient commodity distribution system.

2. The purpose and objectives of the study, the planned results

The purpose of this work is to develop algorithms that will make it possible to most effectively make plans for loading goods, taking into account its distribution along the axes of freight transport.

The goal of optimization is to reduce costs per unit of cargo, increase efficiency and speed up the process of loading and unloading vehicles.

The efficiency of loading optimization can be determined using various criteria and metrics that reflect key aspects of logistics and transportation. Thus, in order to optimize the process of loading goods into vehicles, it is necessary to develop a target function that takes into account key aspects of logistics operations. The goal is to maximize the cost of the load, while it is necessary to comply with the load standards on the axles, to maximize the space utilization factor. The proposed objective function (Z) takes into account the weighting coefficients (α, β, γ), which allow balancing the relative importance of each metric depending on the specific requirements of the optimization problem:

Z = MC(V, Q) * α + ATLR(W) * β + MSU(V, SV) → Criteropt

From here we have:

  1. MC(V, Q) → max – maximizing the value of the cargo, where:
    • V – cargo volume,
    • Q - the cost of the cargo.
  2. ATLR(W) → min – compliance with axle load standards, where
    • W – load distribution on the axes
  3. 2 (V, SV) → max - Maximizing the space utilization factor, where:
    • V – cargo volume,
    • SV is the space utilization factor.

The work on optimizing the loading of transport is a complex multi-criteria process, and effective results can be achieved using advanced optimization methods and modern information technologies.

3. Research and Development Overview

During the analysis of works devoted to the creation of models and algorithms for three-dimensional packaging, it was determined that heuristic approaches are mainly used to solve such problems. The following heuristic algorithms are most often mentioned in the literature:

3.1 Overview of international sources

In the works of researchers from abroad, the solution of the problem of placing goods inside a vehicle is often considered in the context of the task of building optimal routes, known as the traveling salesman problem. For example, in [15], the author considers the use of 3DVL, 3DVL-AC and 3 LCVRP algorithms, but at the same time highlights the need to refine them to more realistic packaging conditions. In the works of other authors, for example, in [16] and [17], the use of the 3L-CVRP algorithm is also found. In general, 3 LCP includes determining the optimal routes for vehicles, taking into account their load capacity and the requirements for three-dimensional packaging of goods inside the vehicle.

3.2 Overview of national sources

In the study of M.V. Luzan, E.V. Nuzhnova [18], an approach to solving the problem of three-dimensional packaging using a genetic algorithm is considered. The author identifies a set of n placed objects (blocks), i=1, 2,..., n. Each i-th block is characterized by three parameters – width (wi), length (li) and height (hi), as well as orientation (rotation) in three-dimensional space (Fig. 3). An empty placement area (container) is also given, having the shape of a parallelepiped with a given width (W), length (L) and height (H).

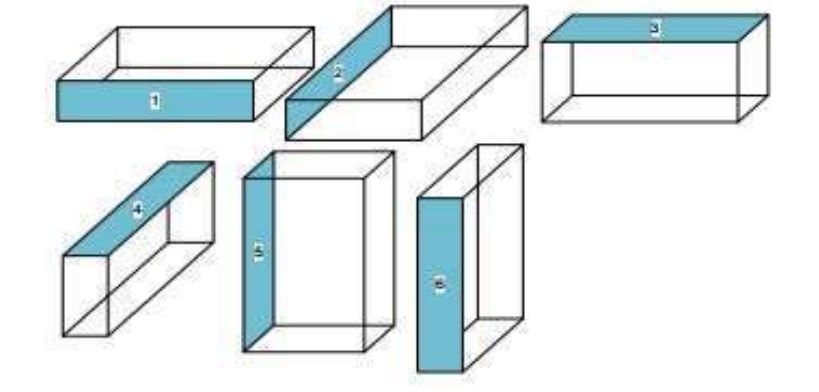
Figure 3 – Possible orientations in space [18]

Each packed block is characterized by two coordinates: and, where the coordinates of the lower left corner (closest to the origin) are written first, and the coordinates with the highest values are written second. Thus, the solution of the problem has the form S={si=(<x1i, y1i, z1i>,<x2i,y2i,z3i>) | i=1,2,…,n}

∑i=1nViV*Q1+P2*Q2+P3*Q3+P4+Q4

As an objective function for the genetic algorithm, the author provides a multi-criteria: where P2 is the ratio of the number of packed blocks in a container to the number of all blocks to be packed; P3 is the number of blocks of the same size packed in a row so that their sides touch; P4 is the ratio the volume of blocks placed on pallets, to the number of pallets; Q1 – the importance factor of the fullness of the container; Q2 – the importance factor of the number of packed blocks in the container; Q3 – the importance factor of packing blocks of the same size with the same sides to each other. The values of the coefficients Q1, Q2, Q3, Q4 are established experimentally. P2, P3 , P4 are calculated when calculating the CF. The task of GA is to maximize the objective function: CF → max

On the other hand, the author of the article [19] proposes a model of potential containers, which provides a representation of the free space of each container as a set of all possible orthogonal objects with the largest overall dimensions that can be placed in it (so-called potential containers, PCs). To correctly place an orthogonal object inside a container, it is necessary that it be placed entirely inside at least one potential container (Fig. 4)

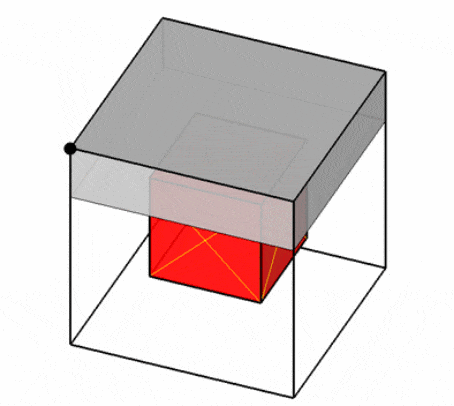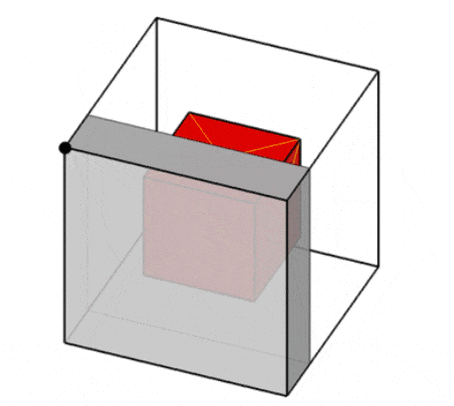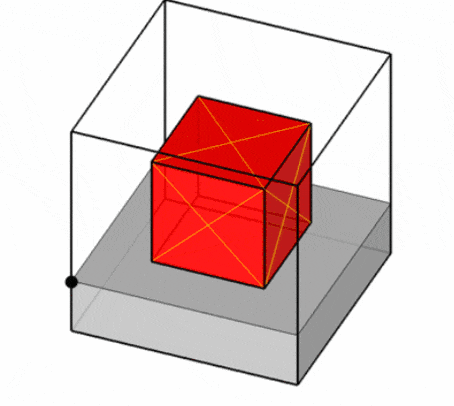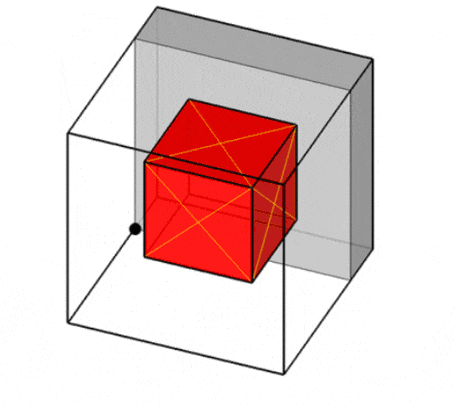
Figure 4 – Examples of placements inside a potential container [19]

4. Mathematical formulation of the problem

As a rule, the car body is represented as a parallelepiped, the inner area of which is set by the parameters of width W, length L and height H. For loading and unloading goods in the body of vehicles, doors are designed, usually located in the end, with a size W1*H1. The vehicle has the property of maximum load capacity D, which can be expressed by a physical property or by applicable law. Let's express the volume V of the body space using the known parameters:

V = W * H * L

Let the goods intended for loading be given by the set of blocks B = {b1, b2, ... bn}, size N. Each block bi can be described by the following parameters: width wi, height hi, length li, weight pi, the cost of ci, etc. You can also express the volume of each block by knowing its parameters:

Vi = wi * hi * li

It is required to calculate the exact position of the blocks in the three-dimensional space of the car body in such a way that its fullness is acceptable, i.e. when all packed blocks are inside the body, do not intersect with each other, have a reliable support in the form of the bottom of the body or other blocks. In this case, the optimization criterion will be considered to maximize the value of the cargo:

∑j=1nbi*ci→max

It is worth highlighting the limitations imposed on this task:

  1. the total volume of each submerged unit must not exceed the volume of the entire vehicle body
    ∑i=0niVi ≤ V
  2. no block can go beyond the limits of the specified volume;
  3. the boxes can only be placed in such a way that their faces are parallel to the walls of the container;
  4. the occupied weight cannot exceed the permissible weight of the cargo:
    Q=min((P3–m3)*S/Z,[(P2–m2)*L/h–mc]*S/(S–Z)) [4],
    where:
    • P3 – Load on the semi-trailer truck, t
    • m3 - the weight of an empty semi–trailer coming to the rear axle, t;
    • S - the distance from the saddle to the axle of the semi-trailer truck, m;
    • Z - the distance from the saddle to the center of gravity of the load, m;
    • P2 - Load on the rear axle of the tractor, t;
    • m2 - the mass of the empty car, which falls on the rear axle, t;
    • L – base of the car;
    • h - the distance from the front axle to the center of gravity of the load, m;
    • mc - the mass of an empty car per saddle unit, t;

List of sources

  1. Kolpakov A.V., Novikov V. N. Optimization of loading and unloading operations as a factor in increasing labor productivity at motor transport enterprises // Service in Russia and abroad.. - 2018. - No.81. - pp. 147-158.
  2. Resolution of the Government of the Russian Federation "On Approval of the Rules for the Carriage of Goods by Road and on Amendments to paragraph 2.1.1 of the Rules of the Road of the Russian Federation" dated December 21, 2020 No. 2200 // Official Publication of Legal Acts. 2020 No. 0001202012230048.
  3. Distribution of cargo along axes during cargo transportation // SGM GROUP company website Access mode: https://sgmtrucks.ru/articles/raspredelenie-gruza-po-osyam-vo-vremya-transportirovki-gruza/.
  4. Zotov L.L. Cargo science: Educational and methodological complex. - St. Petersburg: NWTU, 2008. - 69 p.
  5. Calculation of the permissible load on the axle of a tractor and a semi-trailer // Website of the Semitrailer company.RF Access mode: https://полуприцеп.рф/articles/raschet-dopustimoy-nagruzki-na-os-tyagacha-i-polupritsepa/
  6. Jose Brito, Luiz Ochi , Flavio Montenegro and Nelson Maculan An iterative local search approach applied to the optimal stratification problem // International transactions in operational research . - 2010. - №17. - С. 753-764.
  7. Christos Voudouris, Edward Tsang Guided local search and its application to the traveling salesman problem // European Journal of Operational Research. - 1999. - №113. - С. 469-499.
  8. Jesús Sánchez-Oro, Nenad Mladenovi´, Abraham Duarte General Variable Neighborhood Search for computing graph separators // Springer-Verlag Berlin Heidelberg. - 2014. - №11. - С. 1069-1089.
  9. Kuzjurin N.N. Probabilistic analysis of the greedy algorithm // Proceedings of the Institute of System Programming of the Russian Academy of Sciences. - 2004. - pp. 101-108.
  10. Semenkina Olga Evgenyevna, Popov Evgeny Alexandrovich, Semenkina Olga Ernestovna Self-configuring Evolutionary algorithms for traveling salesman problem // Siberian Aerospace Journal. - 2013. - No. 50. - pp. 134-139.
  11. Anusha Murali, Evan Chandran, Susan Seagroves Optimizing Interplanetary Travel Using a Genetic Algorithm // Journal of Emerging Investigators. - 2018.
  12. Ant Colony Optimization for the Traveling Salesman Problem // Strikingloo User's blog Access mode: https://strikingloo.github.io/ant-colony-optimization-tsp
  13. S. Kirkpatrick; C. D. Gelatt; M. P. Vecchi Optimization by Simulated Annealing // Science. - 1983. - №4598. - С. 671-680.
  14. Sumanta Basu Tabu Search Implementation on Traveling Salesman Problem and Its Variations: A Literature Survey // American Journal of Operations Research. - 2012. - №2. - С. 163-173.
  15. Batoul Mahvash Mohammadi Three-dimensional Capacitated Vehicle Routing Problem With Loading Constraints: dis. Dr. T.N. - Montreal, Quebec, Canada, 2014. - 131 p.
  16. Luis Miguel Escobar-Falcón, David Álvarez-Martínez, Mauricio Granada-Echeverri, John Willmer Escobar, Rubén Augusto Romero-Lázaro A matheuristic algorithm for the three-dimensional loading capacitated vehicle routing problem (3L-CVRP) // Rev. Téc. Ing. Univ. Zulia. - 2017. - №2. - С. 01-14.
  17. Manuel Iori, Silvano Martello Routing problems with loading constraints // Ministero dell’Istruzione, dell’Universit`a e della Ricerca. - 2017. - С. 01-14.
  18. Lutsan M.V., Nuzhnov E.V. Solving the problem of three-dimensional packaging with palletizing containers // Izvestiya SFU. Technical sciences. - 2014. - pp. 196-204.
  19. Chekanin V.A. Development of methods for solving problems of dense packing of objects of arbitrary shape and various dimensions : abstract. dis. ... Doctor of Technical Sciences: 05.01.01. - M., 2021. - 40 p.
  20. Trubachev D.S. The system of forming a dynamic flight schedule, taking into account the airline's air resources // — Access mode: https://masters.donntu.ru/2013/fknt/trubachev/
  21. Lobkova A.A. Intelligent system for optimizing the loading of goods in the conditions of a transport enterprise // — Access mode: https://masters.donntu.ru/2016/fknt/lobkova
  22. Packer3D company's website // — Access mode: https://packer3d.com
  23. TruckLoader company website // — Access mode: https://tlrun.com/en/
  24. Psiola V.V. On one approximation of dense packaging: abstract of the dissertation of the Candidate of Technical Sciences: 05.13.17. - M., 2011. - 17 p.