Реферат по теме выпускной работы
Содержание
- Введение
- 1. Описание проблемы и ее актуальность
- 2. Цель и задачи исследования, планируемые результаты
- 3. Обзор исследований и разработок
- 3.1 Обзор международных источников
- 3.2 Обзор национальных источников
- 3.3 Обзор локальных источников
- 4. Анализ аналогичных систем
- 5. Математическая постановка задачи
- Список источников
Введение
На текущий момент транспортировка товаров является основополагающим моментом в любой производственной компании. Корректный расчет погрузки товара является одним из важнейших этапов при транспортировке товаров, поскольку от качества выполнения данного этапа будет зависеть эффективность выполнения доставки в целом. Не редки случаи, когда из-за некорректного расчета часть товаров осталась не догруженной или оказалась не в той части кузова, в которой должна быть. Подобные ошибки существенно увеличивают время и стоимость транспортировки товаров. Для решения данной проблемы необходимо разработать специализированное программное обеспечение, которое будет автоматически рассчитывать наиболее эффективные способы погрузки товаров и давать рекомендации для улучшения скорости и качества транспортировки.
1. Описание проблемы и ее актуальность
Доставка товаров (грузов) – одна из ключевых логистических функций, связанная с перемещением продукции транспортным средством по определенной технологии в цепи поставок и состоящая из логистических операций и функций, включая экспедирование, грузопереработку, упаковку, передачу прав и собственности на груз, страхование рисков, таможенные процедуры и т.п.
Автомобильный транспорт в отличие от других видов обладает высокой маневренностью и мобильностью, а во многих случаях является единственно возможным видом транспорта, обеспечивающим доставку грузов непосредственно из сферы производства в сферу потребления без участия других видов транспорта.
Основным недостатком автомобильного транспорта является сравнительно высокая себестоимость перевозок, плата за которые обычно взимается по максимальной грузоподъемности автомобиля. К другим недостаткам этого вида транспорта относят низкий уровень механизации погрузочно-разгрузочных работ.
Для увеличения грузооборота транспорта в отраслях экономики необходимо резко снизить ручной труд и количество перегрузочных операций при движении товара по цепочке: товаропроизводитель – складские помещения – розничная торговля. Обеспечить данные цели возможно при изменении технологии перевозочного процесса путем внедрения в этот процесс транспортно-технологических систем [1].
Одной из наиболее существенных проблем, встречаемых в логистической цепочке, является срыв загрузки. Задержки в планировании размещения груза в транспортных средствах могут вызвать не только операционные трудности, но и привести к финансовым потерям, негативным экологическим последствиям и даже повышению риска дорожно-транспортных происшествий.
В современном законодательстве в области транспортировки грузов существуют жесткие нормативы, регулирующие весовые ограничения на различные типы транспортных средств. В соответствии с постановлением Правительства Российской Федерации от 21.12.2020 N 2200 [2], установлены максимально допустимые грузоподъемности в зависимости от количества осей, что направлено на обеспечение безопасности и устойчивости транспортных средств в движении.
Однако важным аспектом в обеспечении безопасности и стабильности транспортных средств является не только соблюдение максимальных грузоподъемностей, но и правильное распределение нагрузки на отдельные оси. Это предотвращает избыточное давление на одни оси и недостаточное на другие, что может существенно повлиять на устойчивость и безопасность движения. На рисунке 1 указано корректное распределение нагрузки вдоль полуприцепа (рис. 1) [3].
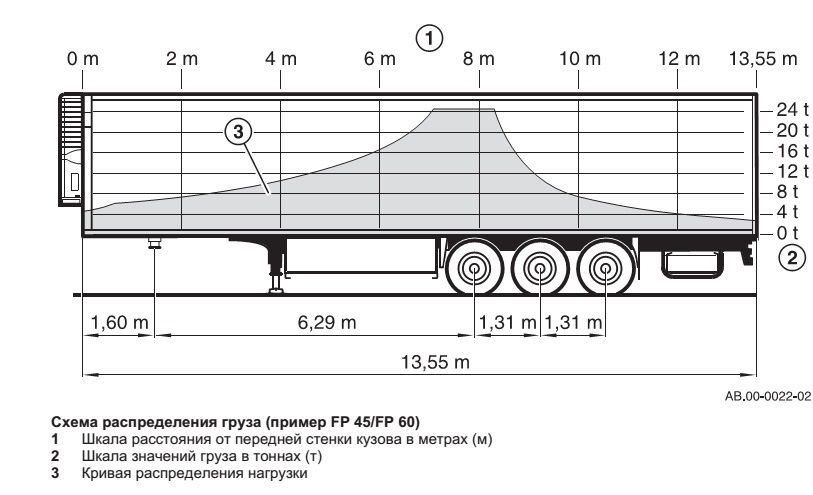
Рисунок 1 – Схема распределения массы груза [3]
Обычно в кузове автотранспортного средства перевозят на стандартных поддонах. При однородном грузе это позволяет считать его массу равномерно распределённой по длине кузова с центром тяжести в базе автомобиля и использовать для расчёта осевых нагрузок и допустимой по эксплуатационным ограничениям полезной нагрузки схемы, представленные на рис. 2 (а, б) [4]. Есть много особенностей, которые оказывают влияние на финальный результат расчетов. Важно для получения правильных расчетов, чтобы подвеска автомобиля была исправной, сделана балансировка, схождение и развал колес настроены правильно. Принципиально не допускать прогибов прицепа под весом груза и обеспечить ровную поверхность грузовой платформы [5]
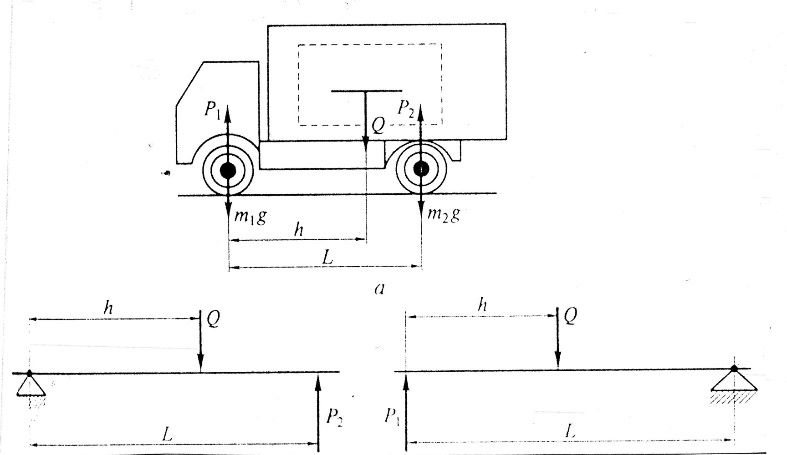
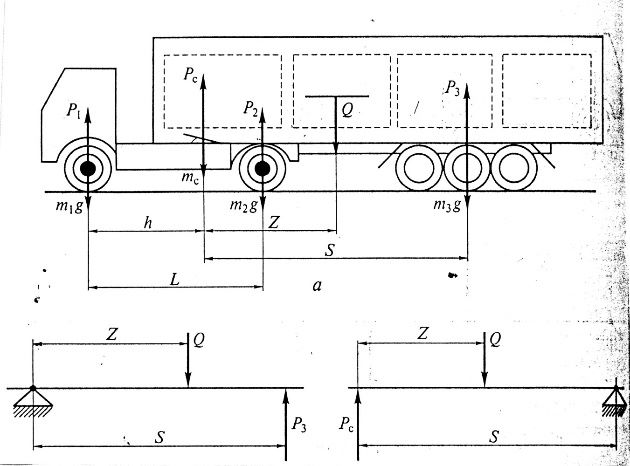
Рисунок 2 – Схемы для расчета допустимой массы груза [4]:
а – в кузове автомобиля; б – в кузове автопоезда
Несмотря на эти регулирования, проблема правильного распределения груза в транспортных средствах остается актуальной. Загрузка полуприцепов максимально допустимыми объемами груза требует особого внимания к распределению массы, чтобы предотвратить неравномерное давление на оси и, следовательно, соблюсти нормативы и обеспечить безопасность перевозок.
В этом контексте, решение проблемы оптимизации погрузки транспорта с учетом равномерного распределения нагрузки на оси приобретает не только экономическое, но и социальное значение. Оно направлено на повышение эффективности логистических процессов, сокращение времени погрузочно-разгрузочных операций и соблюдение стандартов безопасности, что, в свою очередь, способствует более устойчивой и эффективной системе товародвижения.
2. Цель и задачи исследования, планируемые результаты
Целью данной работы является разработка таких алгоритмов, которые позволят наиболее эффективно составлять планы погрузки товара с учетом распределения его по осям грузового транспорта.
Цель оптимизации – снизить расходы на единицу груза, повысить эффективность и ускорить процесс погрузки и разгрузки транспортных средств.
Эффективность оптимизации погрузки может быть определена с использованием различных критериев и метрик, которые отражают ключевые аспекты логистической деятельности и транспортировки. Таким образом, для оптимизации процесса погрузки грузов в транспортные средства необходимо разработать целевую функцию, учитывающую ключевые аспекты логистических операций. Целью является максимизация стоимости груза, при этом необходимо соблюдать нормативы нагрузки на оси, максимизировать коэффициент использования пространства. В предлагаемой целевой функции (Z) учтены весовые коэффициенты (α, β, γ), позволяющие балансировать относительную важность каждой метрики в зависимости от конкретных требований задачи оптимизации:
Z = MC(V, Q) * α + ATLR(W) * β + MSU(V, SV) → Criteropt
Отсюда имеем:
-
MC(V, Q) → max – максимизация стоимости груза, где:
- V – объем груза,
- Q – стоимость груза.
-
ATLR(W) → min – соблюдение нормативов нагрузки на оси, где
- W – распределение нагрузки по осям
- 2
(V, SV) → max - Максимизация коэффициента использования пространства, где:
- V – объем груза,
- SV – коэффициент использования пространства.
Работа над оптимизацией погрузки транспорта является сложным многокритериальным процессом, и эффективные результаты могут быть достигнуты с использованием передовых методов оптимизации и современных информационных технологий.
3. Обзор исследований и разработок
В ходе анализа работ, посвященных созданию моделей и алгоритмов трёхмерной упаковки определено, что для решения подобных задач используют, в основном, эвристические подходы. В литературе наиболее часто упоминаются следующие эвристические алгоритмы:
- итерационный локальный поиск (Iterative Local Search, ILS) [6];
- направленный локальный поиск (Guided Local Search, GLS) [7];
- поиск с переменной окрестностью (Variable Neighborhood Search, VNS) [8];
- вероятностный жадный алгоритм (GRASP) [9];
- эволюционный алгоритм (Evolutionary Algorithm, EA) [10];
- генетический алгоритм (Genetic Algorithms, GA) [11];
- алгоритм оптимизации муравьиной колонии (Ant Colony Optimization, ACO) [12];
- имитация отжига (Simulated Annealing, SA) [13];
- поиск с запретами (Tabu Search, TS) [14].
3.1 Обзор международных источников
В трудах исследователей из-за рубежа решение задачи по размещению грузов внутри транспортного средства часто рассматривается в контексте задачи построения оптимальных маршрутов, известной как проблема коммивояжера. Например, в работе [15] автор рассматривает использование алгоритмов 3DVLP, 3DVLP-AC и 3L-CVRP, но при этом выделяет необходимость их доработки под более реалистичные условия упаковки. В работах других авторов, например, в [16] и [17] также встречается использование алгоритма 3L-CVRP. В общем случае 3L-CVRP включает в себя определение оптимальных маршрутов для транспортных средств с учетом их грузоподъемности и требований по трехмерной упаковке грузов внутри транспортного средства.
3.2 Обзор национальных источников
В исследовании М.В. Луцан, Е.В. Нужнова [18] рассмотрен подход к решению задачи трехмерной упаковки с помощью генетического алгоритма. Автор выделяет множество n размещаемых объектов (блоков), i=1, 2,…, n. Каждый i-й блок характеризуют три параметра – ширина (wi), длина (li) и высота (hi), также ориентация (поворот) в трехмерном пространстве (рис. 3). Также дана пустая область размещения (контейнер), имеющая форму параллелепипеда с заданной шириной (W), длиной (L) и высотой (H).
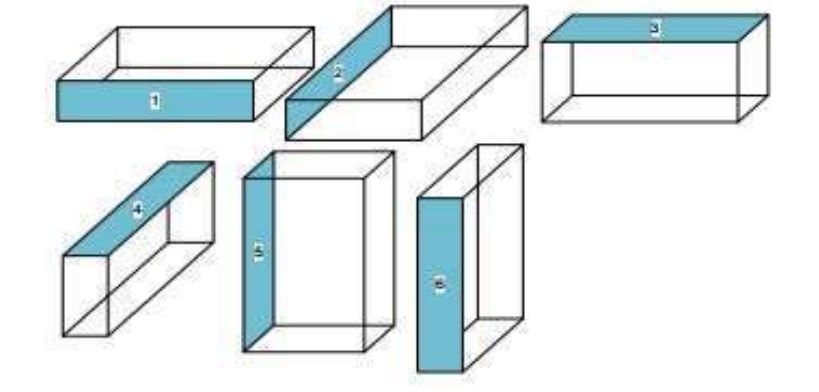
Рисунок 3 – Возможные ориентации в пространстве [18]
Каждый упакованный блок характеризуется двумя координатами: и , где первыми записаны координаты нижнего левого угла (наиболее близкого к началу координат), а вторыми – координаты с наибольшими значениями. Таким образом, решение задачи имеет вид S={si=(<x1i, y1i, z1i>,<x2i,y2i,z3i>) | i=1,2,…,n}
В качестве целевой функции для генетического алгоритма, автор приводит многокритериальную: где P2 – отношение числа упакованных блоков в контейнер к числу всех блоков, подлежащих упаковке; P3 – число блоков одного размера, упакованных подряд так, что их стороны соприкасаются; P4 – отношение объема блоков, размещенных на палетах, к числу палет; Q1 – коэффициент важности заполненности контейнера; Q2 – коэффициент важности числа упакованных блоков в контейнер; Q3 – коэффициент важности упаковки блоков одного размера с одинаковыми сторонами друг к другу. Значения коэффициентов Q1, Q2, Q3, Q4 устанавливаются экспериментально. P2, P3 , P4 вычисляются при расчёте ЦФ. Задача ГА – максимизация целевой функции: ЦФ → max
С другой стороны, автор статьи [19] предлагает модель потенциальных контейнеров, которая обеспечивает представление свободного пространства каждого контейнера в виде набора всех возможных ортогональных объектов с наибольшими габаритными размерами, которые могут быть в нём размещены (так называемых потенциальных контейнеров, ПК). Для корректного размещения ортогонального объекта внутри контейнера необходимо, чтобы он был размещён целиком внутри хотя бы одного потенциального контейнера (рис. 4)
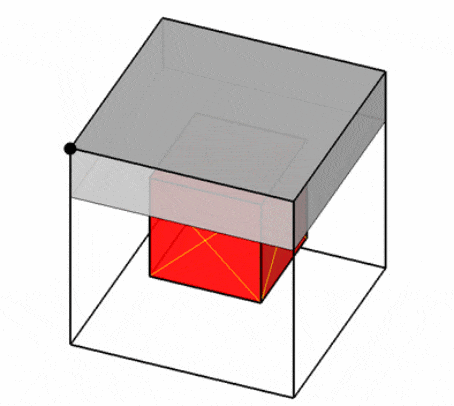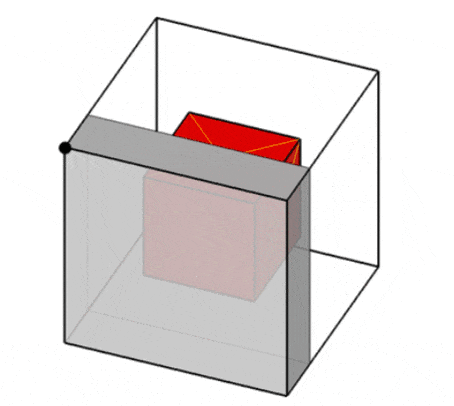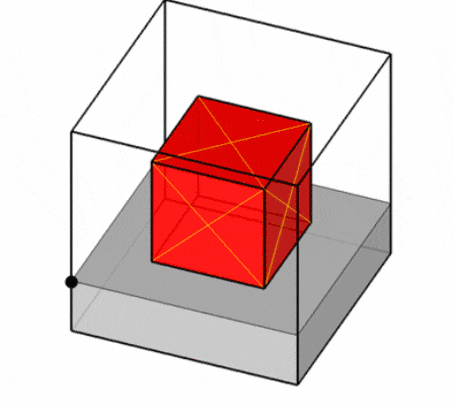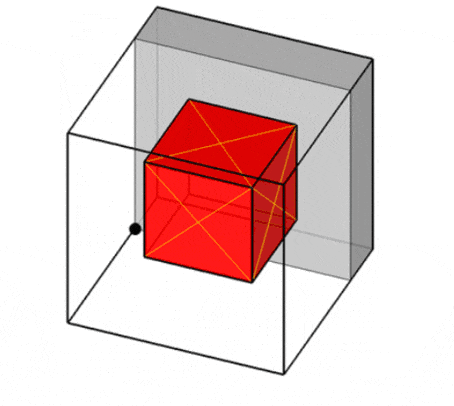
Рисунок 4 – Примеры размещений внутри потенциального контейнера [19]
Однако рассмотренные работы чаще всего не учитывают ограничения реальных задач. Упаковка происходит по принципу максимального использования свободного пространства. Такой принцип подходит, например, для грузоперевозок в контейнерах на судах, однако для грузоперевозок на полуприцепах автотранспорта необходимо учитывать физические возможности и действующее законодательство.
3.3 Обзор локальных источников
В Донецком национальном техническом университете оптимизацию погрузки товаров исследовал Трубачев Д.С. Его научные исследования были посвящены задаче распределения грузов внутри воздушного транспортного средства, с фокусом на эффективном решении проблемы погрузки с учетом ограничений грузоподъемности самолета. В ходе его работы были предложены и рассмотрены четыре метода решения данной сложной задачи: полный перебор, метод ветвей и границ, метод динамического программирования и генетический алгоритм. [20].
Также Лобкова А.А. занималась исследованием оптимальной погрузки товара в условиях транспортного предприятия. Автор предложила использовать алгоритм, который оценивает все виды коробок и их ориентации, что бы открыть новый слой. Как только первая коробка помещена в параллелепипед, она автоматически формирует слой, который будет заполняться по высоте. В зависимости от размеров коробки и параллелепипеда все пространство разбивается на параллелепипедные области [21].
4. Анализ аналогичных систем
В ходе анализа аналогичных компьютерных систем были найдены программные решения Packer3D
[22] и TruckLoader
[23].
Packer3D
использует алгоритмы для расчета оптимального плана размещения разнотипного груза в различных контейнерах, в том числе и автотранспорте.
В основе алгоритма лежат прикладные исследования Псиолы В.В [24]. Программа работает с большим количеством ограничений, строит трехмерную схему погрузки.
TruckLoader
система предназначена для загрузки автомобильного транспорта. Имеются функции для создания конфигурации автотранспорта по фотографии.
Система строит оптимальный план погрузки товара с учетом нагрузки на оси.
5. Математическая постановка задачи
Как правило, кузов автомобиля представляется в виде параллелепипеда, внутренняя область которого задается параметрами ширины W, длины L и высоты H. Для погрузки и разгрузки товаров в кузове автотранспорта предназначены двери, расположенные, как правило, в торце, размером W1*H1. Автотранспортное средство обладает свойством максимальной грузоподъемности D, которое может быть выражено физическим свойством или действующим законом. Выразим объем V пространства кузова, используя известные параметры:
V = W * H * L
Пусть товар, предназначенный для погрузки, задан множеством блоков B = {b1, b2, … bn}, размером N. Каждый блок bi можно описать следующими параметрами: ширина wi, высота hi, длина li, вес pi, стоимость ci и др. Также можно выразить объем каждого блока, зная его параметры:
Vi = wi * hi * li
Требуется рассчитать точное положение блоков в трехмерном пространстве кузова автомобиля таким образом, чтобы его заполненность была допустимой, т.е. когда все упакованные блоки находятся внутри кузова, не пересекаются между собой, имеют надежную опору в виде дна кузова или других блоков. При этом критерием оптимизации будем считать максимизацию стоимости груза:
Стоит выделить ограничения, налагаемые на данную задачу:
- cуммарный объем каждого погруженного блока не должен превышать объема всего кузова ТС:
- ни один блок не может выходить за границы заданного объема;
- коробки могут размещаться только таким образом, чтобы их грани были параллельны стенам контейнера;
- занятый вес не может превышать допустимой массы груза:
[4],
где:
- P3 – Нагрузка на тележку полуприцепа,т
- m3 – масса пустого полуприцепа, приходящая на заднюю ось, т;
- S - расстояние от седла до оси тележки полуприцепа, м;
- Z – расстояние от седла до центра тяжести груза, м;
- P2 - Нагрузка на заднюю ось тягача, т;
- m2 - масса пустого автомобиля, приходящаяся на заднюю ось, т;
- L – база автомобиля;
- h – расстояние от передней оси до центра тяжести груза, м;
- mc – масса пустого автомобиля, приходящаяся на седельное устройство, т;
Список источников
- Колпаков А. В., Новичков В. Н. Оптимизация погрузочно-разгрузочных работ как фактор повышения производительности труда на автотранспортных предприятиях // Сервис в России и за рубежом.. - 2018. - №81. - С. 147-158.
- Постановление правительства Российской Федерации "Об утверждении правил перевозок грузов автомобильным транспортом и о внесении изменений в пункт 2.1.1 правил дорожного движения Российской Федерации" от 21 декабря 2020 г. № 2200 // Официальное опубликование правовых актов. 2020 г. № 0001202012230048.
- Распределение груза по осям во время транспортировки груза // Сайт компании SGM GROUP Режим доступа: https://sgmtrucks.ru/articles/raspredelenie-gruza-po-osyam-vo-vremya-transportirovki-gruza/.
- Зотов Л.Л. Грузоведение: Учебно – методический комплекс. - СПб.: СЗТУ, 2008. - 69 с.
- Расчет допустимой нагрузки на ось тягача и полуприцепа // Сайт компании Полуприцеп.рф Режим доступа: https://полуприцеп.рф/articles/raschet-dopustimoy-nagruzki-na-os-tyagacha-i-polupritsepa/
- Jose Brito, Luiz Ochi , Flavio Montenegro and Nelson Maculan An iterative local search approach applied to the optimal stratification problem // International transactions in operational research . - 2010. - №17. - С. 753-764.
- Christos Voudouris, Edward Tsang Guided local search and its application to the traveling salesman problem // European Journal of Operational Research. - 1999. - №113. - С. 469-499.
- Jesús Sánchez-Oro, Nenad Mladenovi´, Abraham Duarte General Variable Neighborhood Search for computing graph separators // Springer-Verlag Berlin Heidelberg. - 2014. - №11. - С. 1069-1089.
- Kuzjurin N.N. Probabilistic analysis of the greedy algorithm // Труды Института системного программирования РАН. - 2004. - С. 101-108.
- Semenkina Olga Evgenyevna, Popov Evgeny Aleksandrovich, Semenkina Olga Ernestovna Self-configuring Evolutionary algorithms for travelling salesman problem // Сибирский аэрокосмический журнал. - 2013. - №50. - С. 134-139.
- Anusha Murali, Evan Chandran, Susan Seagroves Optimizing Interplanetary Travel Using a Genetic Algorithm // Journal of Emerging Investigators. - 2018.
- Ant Colony Optimization for the Traveling Salesman Problem // Блог пользователя Strikingloo Режим доступа: https://strikingloo.github.io/ant-colony-optimization-tsp
- S. Kirkpatrick; C. D. Gelatt; M. P. Vecchi Optimization by Simulated Annealing // Science. - 1983. - №4598. - С. 671-680.
- Sumanta Basu Tabu Search Implementation on Traveling Salesman Problem and Its Variations: A Literature Survey // American Journal of Operations Research. - 2012. - №2. - С. 163-173.
- Batoul Mahvash Mohamma Three-dimensional Capacitated Vehicle Routing Problem With Loading Constraints: дис. д-р т.н. - Montreal, Quebec, Canada, 2014. - 131 с.
- Luis Miguel Escobar-Falcón, David Álvarez-Martínez, Mauricio Granada-Echeverri, John Willmer Escobar, Rubén Augusto Romero-Lázaro A matheuristic algorithm for the three-dimensional loading capacitated vehicle routing problem (3L-CVRP) // Rev. Téc. Ing. Univ. Zulia. - 2017. - №2. - С. 01-14.
- Manuel Iori, Silvano Martello Routing problems with loading constraints // Ministero dell’Istruzione, dell’Universit`a e della Ricerca. - 2017. - С. 01-14.
- Луцан М.В., Нужнов Е.В. Решение задачи трехмерной упаковки с палетированием контейнеров // Известия ЮФУ. Технические науки. - 2014. - С. 196-204.
- Чеканин В.А. Развитие методов решения задач плотной упаковки объектов произвольной формы и различной размерности : автореф. дис. ... д-р техн. наук: 05.01.01. - М., 2021. - 40 с.
- Трубачев Д.С. Система формирования динамического расписания рейсов, с учетом воздушных ресурсов авиакомпании // — Режим доступа: https://masters.donntu.ru/2013/fknt/trubachev/
- Лобкова А.А. Интеллектуальная система оптимизации погрузки товара в условиях транспортного предприятия // — Режим доступа: https://masters.donntu.ru/2016/fknt/lobkova
- Сайт компании «Packer3D» // — Режим доступа: https://packer3d.com
- Сайт компании «TruckLoader» // — Режим доступа: https://tlrun.com/ru/
- Псиола В.В. Об одном приближении плотной упаковки: автореф. дис. ... канд. техн. наук: 05.13.17. - М., 2011. - 17 с.
