Аннотация
Ткаченко Д.С., Перинская Е.В. Кластерный анализ и алгоритмы кластеризации данных. В статье представлено описание кластерного анализа. Описаны цели и задачи кластеризации. Были проведены классификация и обзор алгоритмов кластеризации данных, таких как: иерархической кластеризации; квадратичной ошибки; с-средних; k-средних; основанные на теории графов; минимального покрывающего дерева. Представлена вычислительная сложность алгоритмов.
Введение
Одна из самых основных способностей живых существ включает в себя группировку сходных объектов для получения классификации [1]. Идея сортировки похожих вещей по категориям явно примитивна, поскольку древний человек, например, должен был быть способен осознать, что многие отдельные объекты обладали определенными свойствами, такими как съедобность, ядовитость, свирепость и так далее.
Классификация, в самом широком смысле этого слова, необходима для развития языка, который состоит из слов, помогающих нам распознавать и обсуждать различные типы о событиях, предметах и людях, с которыми мы сталкиваемся. Например, каждое существительное в языке, по сути, является ярлыком, используемым для описания класса вещей, которые имеют поразительные общие черты; так, животных называют кошками, собаками, лошадьми и т.д., и такое название объединяет индивидов в группы. Присвоение имен и классификация, по сути, синонимичны.
Классификация не только является основной концептуальной деятельностью человека, но и является фундаментальной для большинства отраслей науки. Классификация может включать людей, животных, химические элементы, звезды и т.д. в качестве объектов, подлежащих группировке.
Понятие и задачи кластеризации
Кластерный анализ или кластеризация – это задача группировки набора объектов таким образом, чтобы объекты в одной группе (называемой кластером) были более похожи (в некотором смысле) друг на друга, чем объекты в других группах (кластерах) [2]. Это основная задача исследовательского анализа данных и распространенный метод статистического анализа данных, используемый во многих областях, включая распознавание образов, анализ изображений, поиск информации, биоинформатику, сжатие данных, компьютерную графику и машинное обучение.
Сам по себе кластерный анализ – это не какой-то конкретный алгоритм, а общая задача, которую необходимо решить. Он может быть достигнут с помощью различных алгоритмов, которые существенно различаются в понимании того, что представляет собой кластер и как их эффективно находить. Популярные понятия кластеров включают группы с небольшими расстояниями между членами кластера, плотные области пространства данных, интервалы или особые статистические распределения. Таким образом, кластеризацию можно сформулировать как задачу многоцелевой оптимизации.
Подходящий алгоритм кластеризации и настройки параметров (включая такие параметры, как используемая функция расстояния, пороговое значение плотности или количество ожидаемых кластеров) зависят от индивидуального набора данных и предполагаемого использования результатов. Кластерный анализ как таковой - это не автоматическая задача, а итеративный процесс обнаружения знаний или интерактивной многоцелевой оптимизации, который включает в себя проб и неудач. Часто бывает необходимо изменять предварительную обработку данных и параметры модели до тех пор, пока результат не достигнет желаемых свойств.
Классификация алгоритмов
Были выделены три основных классификации алгоритмов кластеризации [3].
1. На основе иерархии.
Основная идея иерархической кластеризации основана на концепции, согласно которой близлежащие объекты более связаны, чем объекты, находящиеся дальше. Давайте подробнее рассмотрим различные аспекты этих алгоритмов:
- алгоритмы подключаются к «объектам» для формирования «кластеров» на основе их расстояния;
- кластер может быть определен по максимальному расстоянию, необходимому для соединения с частями кластера;
- дендрограммы могут представлять различные кластеры, сформированные на разном расстоянии, что объясняет происхождение названия «иерархическая кластеризация». Эти алгоритмы обеспечивают иерархию кластеров, которые на определенных расстояниях объединяются;
- на дендрограмме ось y обозначает расстояние, на котором кластеры сливаются. Объекты расположены рядом с осью x таким образом, чтобы кластеры не смешивались.
2. На основе центроидов.
При кластеризации центроидов/секционирования кластеры представлены центральным вектором, который не обязательно может быть элементом набора данных. Даже в этом конкретном типе кластеризации необходимо выбрать значение K. Это задача оптимизации: найти количество центроидов или значение K и назначить объекты близлежащим центрам кластеров. Эти шаги необходимо выполнять таким образом, чтобы квадрат расстояния до кластеров был максимальным.
Одним из наиболее широко используемых алгоритмов кластеризации на основе центроида является K-средние, и одним из его недостатков является то, что вам нужно заранее выбирать значение K.
3. На основе плотности.
Кластеризация на основе плотности объединяет области с высокой плотностью примеров в кластеры. Это позволяет получать распределения произвольной формы при условии, что области с высокой плотностью соединены [4]. При работе с данными более высокой размерности и данными различной плотности эти алгоритмы сталкиваются с проблемами. По своей конструкции эти алгоритмы не присваивают кластерам выбросы.
Обзор алгоритмов
Алгоритмы иерархической кластеризации
Алгоритм иерархической кластеризации – это алгоритм обучения без учителя, и это один из самых популярных методов кластеризации в машинном обучении.
Ожидания получения информации от алгоритмов машинного обучения резко возрастают. Изначально мы были ограничены в прогнозировании будущего, предоставляя исторические данные.
Это несложно, когда доступны ожидаемые результаты и особенности исторических данных для построения моделей контролируемого обучения, которые могут предсказывать будущее.
Алгоритмы квадратичной ошибки
Задачу кластеризации можно рассматривать как построение оптимального разбиения объектов на группы. При этом оптимальность может быть определена как требование минимизации среднеквадратической ошибки разбиения, согласно формуле (1):
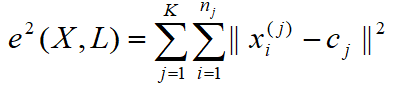
где cj – «центр масс» кластера j (точка со средними значениями характеристик для данного кластера).
К недостаткам данного алгоритма можно отнести необходимость задавать количество кластеров для разбиения.
Нечеткие алгоритмы
В нечеткой кластеризации каждый элемент имеет набор коэффициентов принадлежности, соответствующих степени принадлежности к данному кластеру. Точки, расположенные близко к центру кластера, могут находиться в кластере в большей степени, чем точки на краю кластера. Степень, в которой элемент принадлежит данному кластеру, представляет собой числовое значение, варьирующееся от 0 до 1.
Основное отличие от кластера k-средних заключается в том, что целевая функция для алгоритма нечетких c-средних допускает различное членство в кластере со значениями вероятности, тогда как кластер k-средних имеет строгую целевую функцию, допускающую только одно членство в кластере.
Алгоритмы, основанные на теории графов
Кластеризация графов – это раздел неконтролируемого обучения в рамках машинного обучения, который заключается в разделении узлов графа на сплоченные группы (кластеры) на основе их общих характеристик. Как правило, узлы, назначенные одному кластеру, имеют больше общих свойств друг с другом, чем с узлами в разных кластерах. В зависимости от выбора метода, эти свойства могут быть предопределенными значениями или неявно вычисляться из структуры связности графа.
Определяя кластеризацию графа или в результате кластерного анализа, мы получаем более глубокое понимание его на двух уровнях:
- структура графа в целом;
- сами узлы и взаимосвязи.
Это означает, что различные алгоритмы, связанные с кластеризацией графов, находят применение в различных областях.
Алгоритм минимального покрывающего дерева
Алгоритм Прима – это алгоритм минимального связующего дерева, который помогает определить ребра графа для формирования дерева, включающего каждый узел с минимальной суммой весов, для формирования минимального связующего дерева. Алгоритм Прима начинается с единственного исходного узла, а затем исследует все соседние узлы исходного узла со всеми соединяющими ребрами. Пока мы изучаем графики, мы выберем ребра с минимальным весом и те, которые не могут вызывать циклы в графике. На рисунке 1 изображено минимальное покрывающее дерево, полученное для девяти объектов [5].
Определяя кластеризацию графа или в результате кластерного анализа, мы получаем более глубокое понимание его на двух уровнях:
- структура графа в целом;
- сами узлы и взаимосвязи.
Это означает, что различные алгоритмы, связанные с кластеризацией графов, находят применение в различных областях.
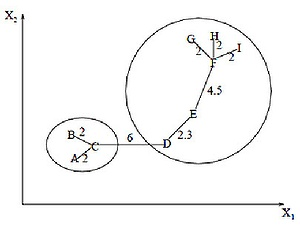
Рисунок 1 – Покрывающее дерево
Выводы
В статье была представлено, что кластеризация помогает понять естественную группировку в наборе данных. Её задачей является проверка того, как распределить информацию по некоторым законным группам. Качество группировки зависит от стратегий и выявления скрытых закономерностей. Самое большое преимущество кластеризации перед классификацией заключается в том, что она может адаптироваться к вносимым изменениям и помогает выделять полезные функции, которые дифференцируют различные группы.
Несмотря на то, что было приведено множество алгоритмов кластеризации и продолжают появляться новые, не существует единого алгоритма кластеризации, который, как было показано, доминировал бы над другими алгоритмами во всех областях применения.
Список использованной литературы
- Воронцов К.В. Алгоритмы кластеризации и многомерного шкалирования. / К.В. Воронцов - Курс лекций. МГУ, 2021. – 520 с.
- Jain A. Data Clustering: A Review. / A. Jain, M. Murty, P. Flynn – ACM Computing Surveys, 2021. – 135 с.
- Котов А. Кластеризация данных / А. Котов, Н. Красильников – М.: Феникс, 2019. – 358 с.
- Мандель И.Д. Кластерный анализ. / И.Д. Мандель – М.: Финансы и Статистика, 2022. – 242 с.
- Айвазян С.А. Прикладная статистика: классификация и снижение размерности. / С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин – М.: Финансы и статистика, 2020. – 269 с.