Рисунок 1 – Верхний график – гистограмма исходного ряда электропотребления, нижний – гистограмма для ряда колебания электропотребления относительно предыдущего часа.
Автор: И.В. Абрамов, Г.Л. Тимонович
Источник: https://elib.bsu.by/
Цель проведенного исследования заключалась в построении прогноза электропотребления на час вперед коллективом искусственных нейронных сетей типа многослойных персептронов.
Исходные данные – почасовое электропотребление Минской областной энергосистемы.
Перечень проведенных задач для построения прогноза потребления электроэнергии нейронной сетью:
Потребление электроэнергии имеет свои шаблоны, которые выражаются в схожем поведении потребления электроэнергии в будние, рабочие и праздничные дни. Выделяя эти шаблоны, можно сделать предположение, что те значения электропотребления, которые имеют явные отклонения от основного распределения данных в шаблонах, являются выбросами. Соответственно, при выделении шаблонов электропотребления и построении доверительных интервалов к этим шаблонам можно идентифицировать предполагаемые выбросы.
При обучении нейронной сети обучающую выборку необходимо масштабировать в некотором интервале, в данном исследовании использовался [–0.5, 0.5] [1]. Наличие выбросов приведет к сдвинутому распределению данных в заданном интервале, что непосредственно влияет на обучение нейронной сети.
Известно, что потребление электроэнергии зависит от температуры погодных условий, поскольку часть вырабатываемой электроэнергии идет на отопительные процессы для поддержания нормальной температуры в помещениях. Следовательно, температура является важным фактором при прогнозировании, однако рассмотрим следующий ряд электропотребления.
Пусть E – исходный временной ряд электропотребления. Тогда временной ряд с лагом (лаг – смещенное значение временного ряда по времени), равным единице, обозначим как El1:
El1 = Ei − Ei−1
(1)
где i — индекс значения электропотребления.
Каждое значение ряда (1) определяется предыдущим, поэтому при часовом прогнозировании потребления электроэнергии на ряде (1) прогнозируется колебание электроэнергии относительно предыдущего часа. Прогнозирование колебания электроэнергии относительно предыдущего часа не является строго зависимым от температурных условий, поскольку уровень электропотребления за предыдущий час уже хранит в себе эту информацию.
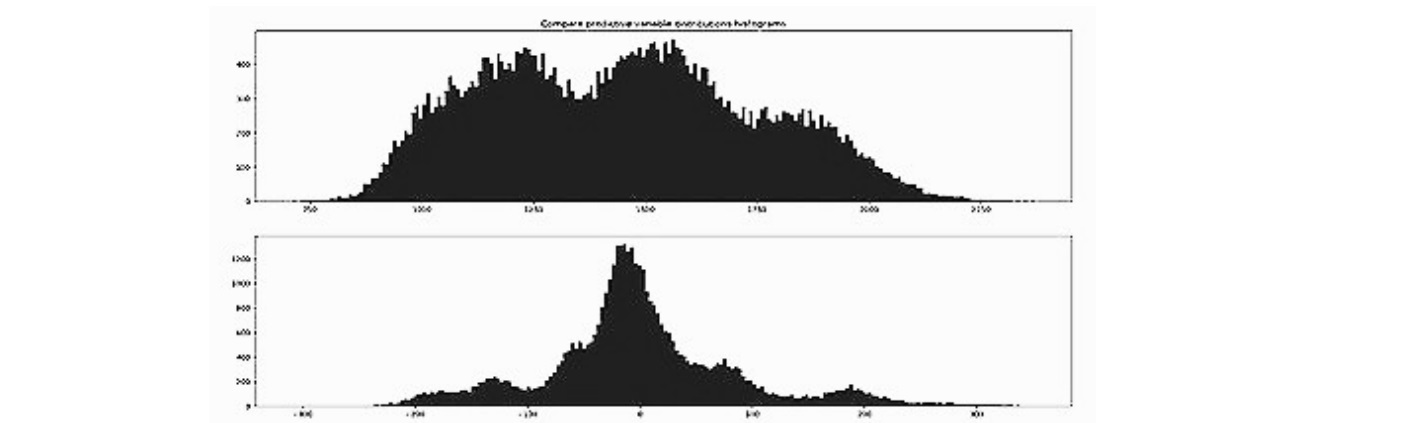
На рис. 1 приведены гистограммы для исходного ряда электропотребления и ряда (1).
Из рис. 1 следует, что распределение электропотребления для ряда (1) близко к нормальному, поэтому является более предпочтительным при прогнозировании. С этой целью в данном исследовании прогнозирование проводилось на временном ряду (1).
В эконометрике при прогнозировании временных рядов принято приводить временной ряд к стационарному виду, в котором среднее значение и дисперсия постоянны, полученные путем удаления трендов исходного временного ряда. Удаление трендов может производиться путем взятия разности временного ряда относительно некоторого лага, при котором наблюдается некоторый тренд. Основные тренды ряда электропотребления: часовой, суточный и недельный тренды. Также присутствует годовой тренд, выражающийся в цикличности температурных погодных условий. Ряд (1) является разностным с лагом, равным единице, то есть показатели корреляции от 1 до 23 лагов будут ниже чем у исходного.
При формировании обучающей выборки использовалась автокорреляционная функция [2] для выделения наиболее значимых лагов временного ряда (1) электропотребления. Так как наиболее значимые лаги электропотребления являются высоко коррелированными, использовался метод главных компонент [2] для снижения размерности обучающего множества и устранения корреляций между лагами электропотребления. Наличие сильно коррелирующих признаков в обучающем множестве понижает информативность обучающего множества и является показателем наличия линейной зависимости между признаками, что может привести к проблеме переобучения нейронной сети [3].
На рис. 2 приведена классическая топология многослойного персептрона с одним скрытым слоем.
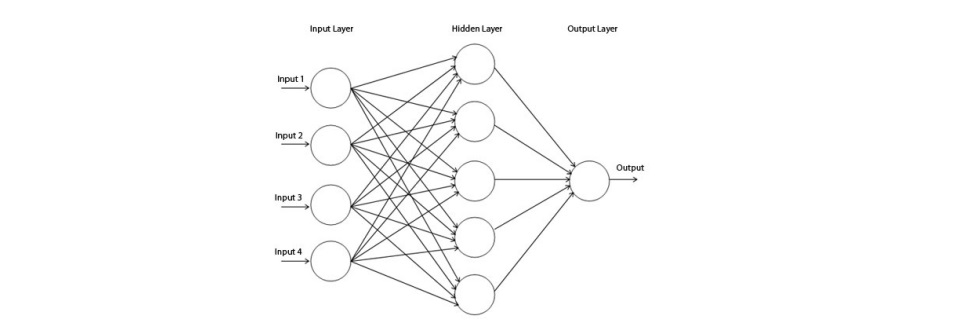
Рассмотрим классическую постановку задачи обучения искусственной нейронной сети с учителем методом обратного распространения ошибки [1]. Дано: множество обучающих признаков ls (2), найти такую модель M (3), которая давала бы наиболее точный прогноз.
ls = { xki, xki+1, ... , xki+n | yk } ,
(2)
M (x, w, φ),
(3)
где i = 1, …., 1…N – количество обучающих элементов в обучающем множестве, xki – обучающий признак, yk – значение электропотребления, прогнозируемой переменной, w, φ – веса и пороговая функция активации нейронной сети соответственно.
Критерий минимизации обучения нейронной сети Q(w):
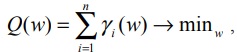
(4)
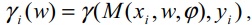
(5)
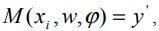
(6)
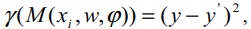
(7)
где γ – функция потерь, y' – предсказание модели M, y – реальное значение электропотребления
Обновление весов нейронной сети:
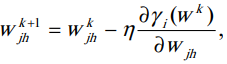
(8)
где η – шаг градиента, k – номер итерации, wkjh – j-ый вес нейрона в скрытом слое h, wk+1jh – обновленный вес.
Следовательно, в процессе обучения нейронной сети обучаемым параметром являются веса ИНС. Изначально веса инициализируются случайным образом, соответственно нейронная сеть приобретает уникальную матрицу весов, и ИНС с различными параметрами (таких как количество скрытых слоев, пороговая функция активации) будут показывать отличающиеся прогнозы в случае недостижения глобального минимума при обучении.
При прогнозировании нейронной сетью нужно определить комплекс параметров, описывающих структуру сети и её методы обучения (например, использование параметров регуляризации), при этом изначально нельзя с достоверностью указать на качество будущих прогнозов при использовании различных комбинаций параметров.
Учитывая проблематику выбора параметров нейронной сети, в данном исследовании создавалось некоторое множество МЛП с различными параметрами. С помощью методики случайного поиска (путем выбора случайным образом различных параметров нейронной сети из некоторого интервала) выбирались те модели МЛП, которые показывали наилучшую способность к обобщению на этапе валидации (промежуточного тестирования). Три лидирующие модели нейронных сетей, имевшие лучшие показатели на этапе валидации, вошли в итоговый коллектив для прогнозирования.
В итоге был реализован следующий алгоритм (рис. 3):
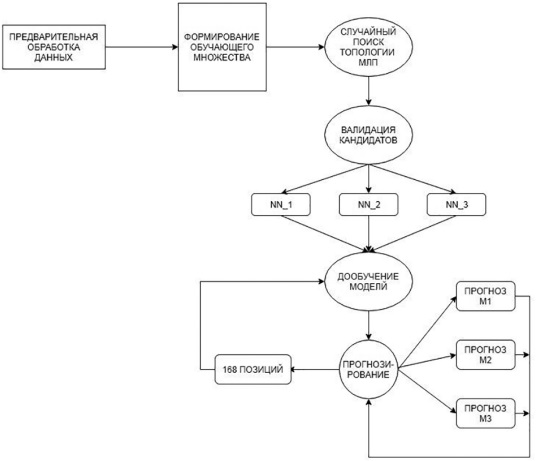
Обучение проводилось по данным 2013–2014 г., валидация – по 2015 г., тестирование – по 2016 г. В итоге три нейронные сети показали следующие результаты почасового прогнозирования в метрике ошибок MAPE (9) на 2016 г.:
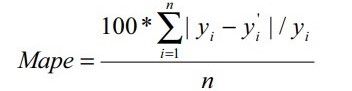
(9)
где n – количество часов в 2016 г., y – фактическое значение электропотребления, y’ – прогнозное.
Средний коллективный прогноз (усредненный прогноз входящих в коллектив моделей МЛП) составил 0,8290 %
В итоге исследования были получены достаточно точные прогнозы электропотребления на час вперед, показано, что прогнозирование коллективом ИНС является более точным, нежели ИНС, участвующими в прогнозе по отдельности.
1. С. Хайкин, Нейронные сети: полный курс 2-е издание / С. Хайкин. – М.: ООО «И.Д. Вильямс», 2016. – 1104 с.
2. А. М. Дубров, Многомерные статистические методы / А. Дубров, В. Мхитарян, Л. Трошин. – М.: Финансы и статистика, 2011. – 352 с.
3. Yoshua, Bengio Practical Recommendations for Gradient-Based Training of Deep Architectures / Y. Bengio // Neural Networks: Tricks of the Trade / Second Edition. Sept. 16th, 2012.