Аннотация
Работа посвящена исследованию задач управления движением колесных роботов. Рассматриваются задачи синтеза траекторий, планирования и реализации движения мобильных роботов — одиночного двухколесного робота и робота, реализованного как змееподобная цепочка двухколесных объектов. Рассмотренные мобильные роботы с двумя независимо управляемыми соосными колесами и одним (возможно, несколькими) пассивным колесом называются роботами «с дифференциальным приводом». Постановка этой задачи определена необходимостью построения динамически корректного и точного управления такими роботами. Рассматриваются динамические характеристики движения роботов, методы управления, вопросы реализации управления на аппаратном уровне, кратко описаны системы сенсорного обеспечения движения роботов.
Введение
В работе рассмотрен ряд взаимосвязанных задач управления мобильными колесными роботами. Рассматриваются задачи планирования и корректной реализации движения мобильных роботов с двумя независимо управляемыми активными колесами и одним или несколькими пассивными колесами, — роботов с дифференциальным приводом. Рассмотрены динамические характеристики движения и обусловленные ими схемы управления такими роботами [2-6]. Актуальность и приложения изучаемых задач определены эффективностью рассматриваемой кинематической схемы. Одно из возможных применений задачи — построение динамически корректного управления роботами-футболистами. Рассмотрены также технические средства реализации управления такими роботами, на примерах описаны средства сенсорного обеспечения их движения.
Ниже на рис.1 в качестве примера приведены фотографии мобильного интеллектуального робота «Аргонавт-3», реализованного в ИПМ им.М.В.Келдыша РАН по схеме «с дифференциальным приводом».
 
Рисунок 1 — Робот «Аргонавт-3»
На рис.1, левая часть, робот показан без внешней декоративной оболочки корпуса, при этом видна схема расположения ведущих колес робота, на том же рисунке справа робот показан в полной версии для задач комплекса «Роботы для людей» [8]. Робот входит в семейство «Аргонавт», роботы семейства оснащены системами управления движения, специализированными инфракрасными локаторами, интеллектуальной сенсорикой, оборудованы техническим зрением, могут нести системы технического слуха, различные специальные системы программного синтеза речи, другие сенсоры.
ДИНАМИКА И УПРАВЛЕНИЕ КОЛЕСНЫМ РОБОТОМ
С ДИФФЕРЕНЦИАЛЬНЫМ ПРИВОДОМ
Рассмотрим робот с двумя независимыми активными колесами, оси которых лежат на одной прямой. Движение такого колесного робота изучалось в статье [1], она дополнена авторами в [2,3]. Изучение движения цепочки подобных объектов приведено в [4]-[6].
Модель
Пусть система представляет собой два абсолютно твердых диска,
находящихся на осях, лежащих на одной прямой, в местах крепления колес
к осям находятся точечные цилиндрические шарниры, колеса управляются
идеальными электродвигателями. К осям жестко прикреплен корпус,
абсолютно твердое тело, которое может двигаться плоскопараллельно. Эта
«тележка» движется по абсолютно шероховатой плоскости, колеса в точках
касания с плоскостью не проскальзывают. Модель рассматриваемого робота
приведена на рис.2. При условии плоскопараллельного движения корпуса
положение системы описывается пятью координатами (x, y, Θ, φ1, φ2),
углы (φ1, φ2) представляют собой углы поворота ведущих колес робота
относительно осей. Центр масс корпуса объекта расположен в точке C
(рис.2). Положение центра масс корпуса С в связанной системе координат
задается вектором b=(b1,b2). Середина расстояния между колесами
обозначена D(x,y). Влияние пассивных колес на движение системы считаем
незначительным.
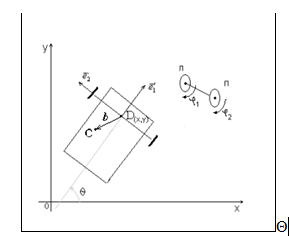
Рисунок 2 — Модели мобильного робота с дифференциальным приводом
Постановка задачи
Пусть начальное состояние системы задано набором, конечное положение определяется набором 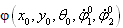 , конечное положение определяется набором (x1, y1, Θ1) . Примем, что во время движения робота координаты (x, y, Θ) вместе с угловыми скоростями вращения колес непрерывны, и , конечное положение определяется набором (x1, y1, Θ1) . Примем, что во время движения робота координаты (x, y, Θ) вместе с угловыми скоростями вращения колес непрерывны, и 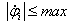 . Рассматривается задача перехода робота из заданного начального состояния в заданное конечное состояние, робот должен перейти в заданную конечную точку с заданной ориентацией продольной оси и заданной скоростью вдоль этой продольной оси в конечной точке. Примеры ситуации, описываемой этой задачей, — выход робота-футболиста на мяч и удар по нему корпусом в заданном направлении с заданной скоростью, движение робота по трассе вида последовательности предварительно заданных точек. . Рассматривается задача перехода робота из заданного начального состояния в заданное конечное состояние, робот должен перейти в заданную конечную точку с заданной ориентацией продольной оси и заданной скоростью вдоль этой продольной оси в конечной точке. Примеры ситуации, описываемой этой задачей, — выход робота-футболиста на мяч и удар по нему корпусом в заданном направлении с заданной скоростью, движение робота по трассе вида последовательности предварительно заданных точек.
Уравнения движения
Исходные уравнения связей, наложенных на систему, и уравнения движения рассматривались в [1], дополняющее исследование проведено в [2-6].
Из условия непроскальзывания колес на плоскости выводятся уравнения связей:
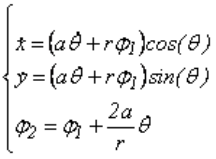
Рассматриваемая система имеет 2 степени свободы, в качестве независимых координат выберем (φ1, Θ). Уравнения движения системы записываются в виде уравнений Чаплыгина:
m0 — масса корпуса робота, m1 — масса колеса робота, m — полная масса робота, J — приведенный момент инерции робота, зависящий от моментов инерции корпуса и колес робота и остальных динамических параметров робота.
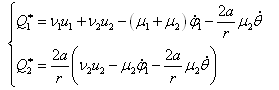
Обобщенные силы описывают действие моментов, создаваемых двигателями постоянного тока, на активные колеса. В (3) коэффициенты ν1, ν2, μ1, μ2 — коэффициенты линейных моделей электродвигателей робота.
Исследование и решение уравнений
Пусть базовыми траекториями робота являются дуги окружностей и отрезки прямых. Рассмотрение непрерывных по скоростям  склеек окружностей, прямых при помощи спиральной кривой первоначально введено в [3]. Основой для введения дополнительной кривой является факт, что при отсутствии такой «склейки» двух траекторий движения в точке их соединения происходит разрыв по скоростям склеек окружностей, прямых при помощи спиральной кривой первоначально введено в [3]. Основой для введения дополнительной кривой является факт, что при отсутствии такой «склейки» двух траекторий движения в точке их соединения происходит разрыв по скоростям  . Это означает неопределенность в управляющих напряжениях и возможность динамических ударов в системе. В общем случае разрыв скоростей возникает на переходе с кривой на кривую, на котором возникает скачок функции ориентированной кривизны траектории: . Это означает неопределенность в управляющих напряжениях и возможность динамических ударов в системе. В общем случае разрыв скоростей возникает на переходе с кривой на кривую, на котором возникает скачок функции ориентированной кривизны траектории:
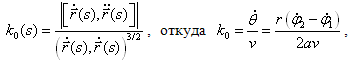
Линейная скорость корпуса робота: 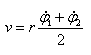
Для того, чтобы исключить разрыв по 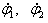 вводится дополнительный режим движения системы на интервале «склейки» [Τ1, Τ2], при котором угловые скорости колес меняются линейно. Соответствующая схема приведена на рис.2. вводится дополнительный режим движения системы на интервале «склейки» [Τ1, Τ2], при котором угловые скорости колес меняются линейно. Соответствующая схема приведена на рис.2.
Соответствующая интервалу [Τ1, Τ2] кривая в координатах (x,y) получается подстановкой линейного закона изменения 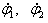 в первое и второе уравнения связей: в первое и второе уравнения связей:
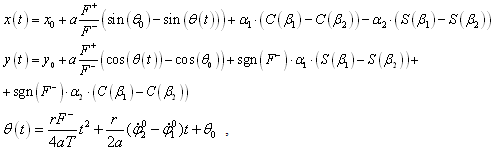
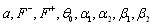 — константы или известные функции времени, — константы или известные функции времени, 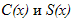 — интегралы Френеля. Получающаяся кривая — — интегралы Френеля. Получающаяся кривая —
обобщенная спираль Корню.
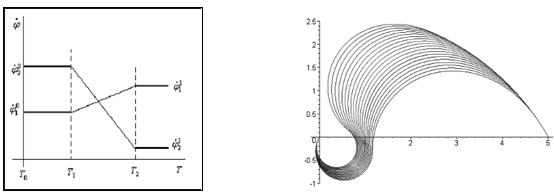
Рисунок 3 — Закон управления. Непрерывная склейка угловых скоростей.
Примеры синтезированных траекторий робота
В [2-3] подробно приведены примеры синтеза траекторий движения робота, состоящих из двух окружностей, соединенных спиральной кривой (рис.3). Эти случаи были также исследованы на предмет минимизации времени движения от точки к точке.
Список литературы
Буданов В.М., Девянин Е.А. «О движении колесных роботов», Прикладная математика и механика, т.67, вып. 2, 2003 г.
Охоцимский Д.Е., Павловский В.Е. «Проблемы динамики и управления мобильных колесных роботов», материалы научной школы-конференции «Мобильные роботы и мехатронные системы», М., МГУ, 2005.
Павловский В.Е., Евграфов В.В. «Синтез D2-гладких траекторий для мобильного робота с дифференциальным приводом», материалы научной школы-конференции «Мобильные роботы и мехатронные системы», М., МГУ, 2004.
Вверх
|