Анализ эффективности многошаговых многоточечных параллельных методов решения задачи Коши для обыкновенных дифференциальных уравнений

Содержание

Введение

1. Типовые структуры линий связи параллельных ВС

   
   

2. Численные методы решения задач Коши для ОДУ

   
   

3. Многошаговые методы решения задач Коши для ОДУ

   
   

   1. Явные многошаговые методы Адамса-Башфорта

      
      

   2. Неявные многошаговые методы Адамса-Мултона

      
      

4. Параллельные методы численного решения задачи Коши для ОДУ

5. Оценка параллелизма многошаговых блочных методов

Выводы

Введение

Если в один и тот же момент времени выполняются одновременно несколько операций обработки данных, то такие вычисления называются параллельными[1]. Потребность решения сложных прикладных задач с большим объемом вычислений и принципиальная ограниченность максимального быстродействия "классических" - по схеме фон Неймана - ЭВМ привели к появлению многопроцессорных вычислительных систем. Использование таких средств вычислительной техники позволяет существенно увеличивать производительность ЭВМ при любом существующем уровне развития компьютерного оборудования. При этом, однако, необходимо "параллельное" обобщение традиционной - последовательной - технологии решения задач на ЭВМ. Так, численные методы в случае многопроцессорных вычислительных систем должны проектироваться как системы параллельных и взаимодействующих между собой процессов, допускающих исполнение на независимых процессорах. Применяемые алгоритмические языки и системное программное обеспечение должны обеспечивать создание параллельных программ, организовывать синхронизацию и взаимоисключение асинхронных процессов.

Проблема создания высокопроизводительных вычислительных систем является одной из наиболее сложных научно-технических задач современности и ее решение возможно только при концентрации усилий многих талантливых ученых и конструкторов, предполагает использование всех последних достижений науки и техники и требует значительных финансовых инвестиций.

1. Типовые структуры линий связи параллельных ВС

Топология ВС – это способ соединения компьютеров в единую ВС.

К числу типовых топологий относят[2]:

- Линейка ( linear array or farm ) – представляет собой линейный массив процессоров (рис.1).

Рисунок 1 – Сеть процессоров с топологией линейка

Система, в которой каждый процессор имеет линии связи только с двумя соседними (с предыдущим и последующим) процессорами; такая схема является, с одной стороны, просто реализуемой, а с другой стороны, соответствует структуре передачи данных при решении многих вычислительных задач (например, при организации конвейерных вычислений);

- Кольцо ( ring ) – данная топология аналогична топологии линейка с тем учетом, что первый и последний компьютер соединены (рисунок 2). Связи в могут быть однонаправленными или двунаправленными. [6] Кольцевая структура сохраняет достоинства, а также сокращает максимальное расстояние между процессорами – n /2 [5].

Рисунок 2 – Сеть с топологией кольцо

- Решетка (2D-решетка, матрица, сетка – mesh) – система, в которой граф линий связи образует прямоугольную сетку, то есть процессоры расположены в виде правильной двумерной решетки и каждый процессор (кроме крайних) соединен с четырьмя соседями (рисунок 3)

Рисунок 3 – Сеть с топологией решетка

Достоинством такой схемы является простота, а недостаток состоит в том, что при обмене между отдаленными процессорами данные должны пройти через ряд промежуточных процессоров.

- Гиперкуб ( hypercube ) – данная топология представляет частный случай решетки, когда по каждой размерности сетки имеется только два процессора (то есть гиперкуб содержит n = 2 N процессоров при размерности N ).

Рисунок 4 – Сеть с топологией 3-х мерный гиперкуб

Также может быть схема соединения процессоров в четырехмерном кубе. Эта схема приведена на рисунке 5.

Рисунок 5 – Сеть с топологией 4-х мерный гиперкуб

Топология гиперкуб предоставляет возможность моделировать некоторые важные типы связей: линейка, кольцо, решетка.

- Клика или полный граф ( completely - connected graph or clique ) – система, в которой связи процессоров образуют полный граф.

Рисунок 6 – Сеть с топологией клика

- Звезда ( star ) – система, в которой все процессоры имеют линии связи с некоторыми управляющим процессором (рисунок 7). Данная топология является эффективной при организации централизованных схем параллельных вычислений.

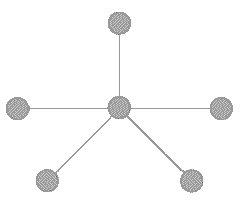
Рисунок 7 – Сеть с топологией звезда

- «Толстое дерево» («fat-tree», hypertree) – архитектура процессоры в которой локализованы в листьях дерева, в то время как внутренние узлы дерева скомпонованы во внутреннюю сеть. Поддеревья могут общаться между собой, не затрагивая более высоких уровней сети. (рисунок 8, 9)

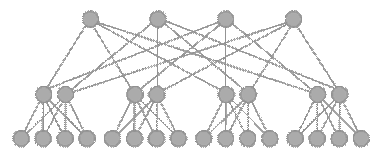
Рисунок 8 – Сеть с архитектурой «Fat-tree»

Рисунок 8 – Сеть с архитектурой «Fat-tree» (вид сверху)

При этом данная топология является наиболее эффективной.

Реальные высокопроизводительные параллельные вычислительные системы обычно используют несколько различных схем соединения процессоров. Это позволяет сочетать лучшие качества известных топологий и минимизировать недостатки. А также, поскольку способ соединения процессоров друг с другом больше влияет на производительность кластера , чем тип используемых в ней процессоров, то может оказаться более целесообразным создать систему из большего числа дешевых компьютеров, чем из меньшего числа дорогих[8].

Решение различных прикладных задач требует решения обыкновенных дифференциальных уравнений или систем обыкновенных дифференциальных уравнений высокого порядка. Сокращение времени решения, а, следовательно, и времени моделирования, возможно при использовании параллельных вычислительных систем, эффективность работы которых существенно зависит от характеристик применяемых параллельных алгоритмов.

2. Численные методы решения задач Коши для ОДУ

Обыкновенным дифференциальным уравнением (ОДУ) называется уравнение вида [3] (в него входят: независимая переменная t, неизвестная x и ее производные по t )

F(t, J(m)x, C) = 0.

В свою очередь, порядком ОДУ называется порядок старшей производной искомой функции.

Общим интегралом уравнения называют функцию , связывающую независимую переменную t, искомую функцию x(t) и n констант интегрирования с помощью уравнения

т.е. решение x(t) входитнеявным образом, причем количество констант интегрирования равно порядку ОДУ

Общим решением ОДУ называется функция

связывающая независимую переменную t и n констант интегрирования C i , т.е. решение x(t) определяется явным образом.

Для определения констант интегрирования С i задаются дополнительные условия в количестве, равном количеству констант интегрирования или порядку ОДУ.

Если в дополнительные условия подставить исходное уравнение и решить полученную систему относительно С i , а затем подставить в общий интеграл, то получим частное решение или частный интеграл

.

Аналогичные процедуры с общим решением (3) дают частный интеграл

Если все дополнительные условия задаются в одной точке x 0 , то совокупность ОДУ и дополнительных условий называют задачей Коши для рассматриваемого ОДУ. В этом случае дополнительные условия называют начальными условиями.

Если дополнительные условия задаются более чем в одной точке, то совокупность ОДУ и дополнительных условий называют краевой задачей Коши для рассматриваемого ОДУ, а дополнительные условия называют граничными или краевыми условиями.

3. Многошаговые методы решения задач Коши для ОДУ

Методы решения ОДУ бывают одношаговые и многошаговые. К одношаговым относятся: метод Эйлера, метод Рунге – Кутты и др., а к многошаговым: линейные многошаговые разностные методы, в том числе методы Адамса-Башфорта и методы Адамса-Мултона.

В многошаговых методах повышение точность вычисления происходит за счет использования информации о поведении решения на предыдущих шагах.

Общая схема построения m-шаговых разностных методов, используемых для приближенного решения задачи Коши [4]

(1)

выглядит следующим образом

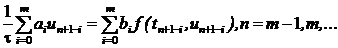(2)

где - числовые коэффициенты, не зависящие от n, причем .Уравнение (2) следует рассматривать как рекуррентное соотношение, выражающее новое значение через найденные ранее значения .

Наиболее простые и наиболее часто встречающиеся вычислительные правила для многошаговых методов имеют вид:

(3)

Среди правил (5) особенно широко известны явные (экстраполяционные) при и неявные (интерполяционные) при методы Адамса.

3.1 Явные многошаговые методы Адамса-Башфорта

Все m –шаговые методы Адамса, полученные из формулы (3), положив в ней получили название явные методы Адамса-Башфорта или э кстраполяционные методы Адамса

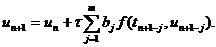(4)

Определить коэффициенты формулы (4) можно следующим образом. Пусть известно приближенное решение в m узлах сетки . Следовательно, в этих точках отрезка известно и значение правой части дифференциального уравнения (1) при i=n-m+1, ...,n-1,n, причем будет уже функцией только одной переменной . Заменим в (6) функцию интерполяционным многочленом , например, многочленом Ньютона и вычислим значение , проинтегрировав (1) на отрезке . Находим

(5)

Проводя интегрирование, получим разностную схему для решения дифференциального уравнения. Порядок схемы определяется величиной остаточного члена интерполяционного полинома. По существу, интерполяционный многочлен в формуле (5) используется вне области, т.е. в данном случае это экстраполяционный многочлен. Поэтому полученный таким образом метод часто называют экстраполяционным методом Адамса - Башфорта. Получим формулы Адамса - Башфорта для различного числа точек m. Зададим таблицу , заданных значений приближенного решения, по которым можно вычислить значения и составить таблицу .

Рассмотрим случай при m =2. В этом случае соответствующий многочлен Ньютона будет иметь вид:

Н1(t)=Fn+(t-tn)F(tn,tn-1)=Fn+(t-tn)(Fn-Fn-1)/h.

Подставив его в формулу (7) мы получим:

А после интегрирования формула для вычисления приближенного решения будет иметь вид:

3. 2 Неявные многошаговые методы Адамса-Мултона

Неявные m-шаговые методы Адамса определяются формулой (6) при . Их также называют интерполяционные методы Адамса-Мултона.

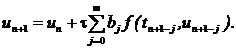(6)

Построение интерполяционных m- шаговых методов Адамса-Мултона может быть осуществлено совершенно аналогично случаю экстраполяционных формул. Для этого следует использовать интеграл (5) , в котором интерполяционный многочлен построен по следующим узлам интерполяции .

Приведем интерполяционные формулы Адамса различных порядков точности:

двухшаговый неявный разностный метод Адамса- Мултона

(7)

трехшаговый неявный разностный метод Адамса – Мултона

(8)

Определение порядка аппроксимации неявных методов Адамса-Мултона выполняется аналогично определению невязки методов Адамса-Башфорта

Погрешность аппроксимации трех шагового метода Адамса – Мултона равна

Заметим, что во всех приведенных выше интерполяционных формулах Адамса значение неизвестно, так как само пока является неизвестным. Следовательно, интерполяционные методы Адамса определяют только неявно. Так, например, интерполяционная формула второго порядка точности

(9)

действительно является уравнением относительно неизвестного значения . Поэтому интерполяционный метод Адамса называют неявным.

На практике обычно не решают уравнение (9), а используют совместно явную и неявную формулы (метод Адамса-Бошфорта-Мултона), что приводит к методу прогноза и коррекции. Одним из широко используемых методов прогноза и коррекции является объединение методов Адамса четвертого порядка точности

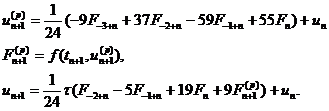(10)

При такой последовательности вычислений этот метод является явным

4 Параллельные методы численного решения задачи Коши для ОДУ

В данной главе будут рассмотрены основы распараллеливания одношаговых и многошаговых алгоритмов методов решения задачи Коши для ОДУ [5].

Для простоты понимания и вывода формул, будем рассматривать решение задачи Коши для одного обыкновенного дифференциального уравнения первого порядка

x'=f(tx),x(t0)=x0()

Множество M точек равномерной сетки { t m }, m = и t m =T с шагом ? разобьем на N блоков, содержащих к точек каждый, при этом k NхM. В каждом блоке введем номер точки i = и обозначим через t n , i точку n блока с номером i. Точку t n ,0 назовем началом блока n, а t n , k - концом блока. Очевидно, что имеет место t n , k = t n +1,0 . Условимся начальную точку t 0 = t 1,0 в блок не включать. При численном решении задачи Коши для каждого следующего блока новые k значений функции вычисляются одновременно. Поэтому блочные методы особенно удачно реализуются на параллельных вычислительных системах.

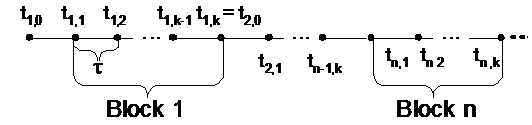
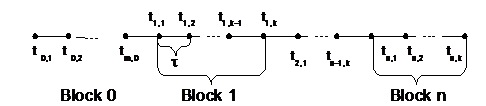
В общем случае уравнения многошаговых разностных методов для блока из k точек при использовании вычисленных значений приближенного решения в m предшествующих блоку узлах, с учетом введенных выше обозначений можно записать в виде:

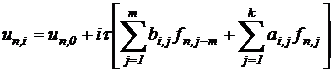, , n =1,2,…

5 Оценка параллелизма многошаговых блочных методов  

Для оценки ускорения m -шагового k -точечного блочного метода сравним время его выполнения на мультипроцессорной системе со временем выполнения алгоритма m -шагового метода Адамса-Башфорта на однопроцессорной ЭВМ. [5] Метод Адамса-Башфорта можно рассматривать как многошаговый одноточечный блочный метод. Последовательное k -кратное применение формул Адамса-Башфорта позволяет вычислить приближенное решение в тех же k узлах блока, в которых параллельно за k итераций может быть вычислено решение m -шаговым k -точечным блочным методом. В этом случае время вычисления будет приблизительно одинаково. Точность приближенного решения, полученного m -шаговым k -точечным блочным методом, имеет порядок O( , а точность приближенного решения, полученного по m шаговой формуле Адамса-Башфорта, имеет порядокO( . Поэтому для получения решения с одинаковой точностью для метода Адамса-Башфорта надо, чтобы шаги сетки для метода Адамса-Башфорта и m -шагового k -точечного блочного метода удовлетворяли условию  

Здесь шаг сетки решения задачи методом Адамса-Башфорта, а шаг сетки решения этой же задачи. Если , например, шаг для решения задачи 4 -шаговым 4 -точечным блочным методом выбран равным =0.01, то для обеспечения той же точности решения методом Адамса-Башфорта необходимо взять шаг =0.0063.В этом случае время решение задачи m -шаговым k -точечным блочным методом будет меньше в 16 раз времени решения методом Адамса-Башфорта. В приведенных здесь оценках не учитывалось время обменов между процессорами при решении на линейке.

ЭВМ и сравним времена решения задачи m -шаговым k -точечным блочным методом на однопроцессорной линейке k процессоров . Закрепим за каждым узлом блока процессор. Используя обозначения, введенные в п. 7.3. получим для времени вычисления на одном процессоре с локальной точностью O( во всех k узлах блока по формулам

Время параллельного вычисления приближенных значений решения на линейке из процессоров с той же точностью для всех узлов блока составит

Ускорение параллельных многоточечных алгоритмов можно вычислиь по формуле

Если учитывать только время вычислений правой части уравнений, т.к. времена выполнения арифметических операций и обмена значительно меньше времени вычисления правой части, то ускорение k точечного многошагового параллельного алгоритма можно считать приближенно равным

и эффективность будет равна

Отсюда следует, что при решении на однопроцессорной ЭВМ решение m -шаговым k -точечным блочным методом потребует меньше времени, чем решение этой же задачи соответствующим методом Адамса - Башфорта.

Выводы

В данный момент все чаще и чаще приходится касаться вопросов вычислительной мощности систем. Одним из способов повышения этой мощности является организация параллельных систем.

В данной работе рассмотрены параллельные алгоритмы решения задачи Коши, как многошаговых, так и одношаговых. Повышение производительности параллельных алгоритмов происходит за счет одновременного вычисления нескольких значений. В свою очередь повышение точности вычислений многошаговых методов происходит за счет учета найденных решений в нахождении новых. Т.о. параллельные многошаговые методы обладают высокой производительностью и высокой точностью вычислений.

Литература

1. Воеводин В.В. Математические основы параллельных вычислений. - М.: Изд-во МГУ, 1991. - 345 с.
   
2. Гергель В.П., Стронгин Р.Г. Основы параллельных вычислений для многопроцессорных вычислительных систем. - Н.Новгород, ННГУ, 2001
   
3. http://www.ict.nsc.ru/rus/textbooks/akhmerov/. Книга Ахмеров Р.Р "Численные методы решения обыкновенных дифференциальных уравнений"
   
4. Фельдман Л.П., Святный В.А. Параллельные алгоритмы моделирования динамических систем, описываемых обыкновенными дифференциальными уравнениями. Научн. тр. ДонГТУ. Вып. 6.– Донецк: ДонГТУ, 1999. – 330с
   
5. Фельдман Л. П. Сходимость и оценка погрешности параллельных одношаговых блочных методов моделирования динамических систем с сосредоточенными параметрами //Науковi працi Донецького державного технiчного унiверситету. Серiя: Проблеми моделювання та автоматизації проектування динамичних систем, випуск 15: – Донецк:, 2000, с. 12 – 16.
   
6. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ- Петербург, 2002
   
7. http://www.intuit.ru/ Интернет-Университет Информационных Технологий
   
8. Самарский А.А., Гулин А.В. Численные методы.- М.: Гл. ред. физ.-мат. лит., 1989.-432 с.
   
9. Ахмеров Р.Р., Садовский Б.Н. Основы теории обыкновенных дифференциальных уравнений