|
Главная
Диссертация Перечень ссылок Отчёт о поиске Индивидуальное задание Библиотека Сайт ДонНТУ Магистры ДонНТУ |
 |
Близкая Ольга Владимировна Факультет: Компьютерных информационных технологий и автоматики (ФКИТА)
|
Автореферат на тему: "Разработка методов и алгоритмов обработки медицинских изображений с использованием методов искусственного интеллекта" 1. Современные проблемы методов обработки медицинских изображений 1. Современные проблемы методов обработки медицинских изображений На сегодняшний день обработка изображений является важным направлением применения современной вычислительной техники. Известны такие задачи обработки изображений, как фильтраци я и восстановление изображений , сегментация изображений, как средства сжатия информации. Проблемы распознав а ния изображений кроме классической задачи распознавания фигур заданной формы на изображении ставят новые задачи распознавания линий и углов на изображении, распознавания края изображения. Для решения всех перечисленных выше задач в последние годы активно используются нейросетевые алгоритмы и нейрокомпьютеры . В своей магистерской работе я также решила заниматься именно использованием нейронных сетей, как нового направления среди методов искусственного интеллекта. В последние десятилетия в мире бурно развивается новая прикладная область математики, специализирующаяся на искусственных нейронных сетях (НС). Актуальность исследований в этом направлении подтверждается массой различных применений НС. Это автоматизация процессов распознавания образов, адаптивное управление, аппроксимация функционалов, прогнозирование, создание экспертных систем, организация ассоциативной памяти и многие другие приложения. С помощью НС можно, например, предсказывать показатели биржевого рынка, выполнять распознавание оптических или звуковых сигналов, создавать самообучающиеся системы, способные управлять автомашиной при парковке или синтезировать речь по тексту. Все эти разработки используют сеть обратного распространения – наиболее успешный, по-видимому, из современных алгоритмов. Обратное распространение является систематическим методом для обучения многослойных сетей, но оно не свободно от проблем. Прежде всего нет гарантии, что сеть может быть обучена за конечное время. Много усилий, израсходованных на обучение, пропадает напрасно после затрат большого количества машинного времени. Когда это происходит, попытка обучения повторяется – без всякой уверенности, что результат окажется лучше. Нет также уверенности, что сеть обучится наилучшим возможным образом. Алгоритм обучения может попасть в «ловушку» так называемого локального минимума и будет получено худшее решение. Разработано много других сетевых алгоритмов обучения, имеющих свои специфические преимущества. Но всё же следует подчеркнуть, что никакая из сегодняшних сетей не является панацеей, все они страдают от ограничений в своих возможностях обучаться . Для улучшения существующих сетей требуется много основательной работы. Должны быть развиты новые технологии, улучшены существующие методы и расширены теоретические основы, прежде чем данная область сможет полностью реализовать свои потенциальные возможности. Обработка изображений является многоплановой задачей. Сюда включают решение задач фильтрации шумов, геометрической коррекции, градационной коррекции, усиления локальных контрастов, резкости, восстановления изображений и др. Методы обработки изображений разделяют на два класса. Первый - методы обработки в частотной области, второй - методы обработки в пространственной области. Методы обработки изображений в частотной области базируются на соответствующих моделях зрения человека, например, модели Стокхема, Ч.Холла и Э.Холла. Эти модели показывают, что эффективное изменение визуального качества изображения можно проводить через изменение двух основных составных частей изображения - низкочастотной (фоновой) и высокочастотной (детальной). Алгоритмы обработки в частотной области имеют большую вычислительную сложность, которая ограничивает их использование для обработки изображений в масштабе реального времени. Однако, линейная фильтрация широко используется в когерентных оптических системах обработки информации, где как и в цифровой обработке, сигналов она базируется на использовании быстрых алгоритмов свертки и спектрального анализа. Параметры необходимых фильтров преимущественно определяют, пользуясь принципами оптимальной (винеровской) фильтрации, разработанной для среднеквадратического критерия качества фильтрации. Достижения теории фильтрации широко используют при обработке изображений. Так, согласующая фильтрация применяется в обработке изображений с позиций не просто повышения качества, а для выявления объектов на изображениях. Реальные системы формирования изображений не являются идеальными из-за аберрации, смазывания изображения во время экспозиции, низкого контраста, наличия атмосферных неоднородностей и т.п. Поэтому для этих систем в предположении их линейности и стационарности можно значительно улучшить качество изображений, применяя технику инверсной фильтрации. Метод инверсной фильтрации никак не учитывает шумовых эффектов, поэтому не удивительно, что он дает плохие результаты при наличии шума. Методы винеровской фильтрации учитывают априорное значение статистических свойств шума и потому позволяют повысить качество возобновляемых изображений. При использовании метода пространственной реставрации изображений на основе регрессии шумовое поле моделируют некоторой реализацией двумерного случайного процесса с неизвестными средним и ковариационной функцией. Тогда применяют винеровское оценивание в предположении, что идеальное изображение также является реализацией двумерного случайного процесса с известными первым и вторым моментами. Представляя результирующее изображение как свертку входного изображения с импульсной передаточной характеристикой или функцией размывания точки оптической системы, которая вносит искажение, для восстановления изображения используют также итерационный алгоритм Бугера-Ван-Циттера. Обобщая сжатый обзор некоторых алгебраических методов восстановления изображений, отметим, что он является составной частью более широкой проблемы решения некорректных задач восстановления изображений, включая реконструкцию изображений по проекциям (реконструктивную томографию). Рядом с этими методами широко используются методы линейной фильтрации для улучшения изображений. Основой большинства методов линейной фильтрации в пространственной области являются ортогональные преобразования. Существует три основных области применения двумерных ортогональных преобразований для обработки изображений. Во-первых, преобразования используют для выделения характеристик признаков изображения. Второй областью применения является кодирование изображений, когда ширина спектра уменьшается за счет отбрасывания или грубого квантования малых по величине коэффициентов преобразования. Третья область применения - это сокращения размерности при выполнении вычислений. К таким преобразованиям принадлежат преобразования Фурье, синусные, косинусные, волновые преобразования, а также преобразования Карунена-Лоева, Уолша, Хаара и Адамара. Однако и эти преобразования не обеспечивают обработки изображений в масштабе реального времени из-за своей вычислительной сложности. Другой подход к обработке изображений с целью улучшения их визуального качества состоит в непосредственном использовании разных фильтров. Область их функционирования - в основном частотная и реже - пространственная. Для этого используют разные методы синтеза фильтров, как одномерных, так и двумерных, чем обеспечивают реализацию заданных частотных характеристик. Проведенный анализ показывает, что использование фильтрации изображений с целью повышения их визуального качества с обеспечением высокого быстродействия является наиболее рациональным при реализации в пространственной области. Однако арсенал алгоритмических средств обработки при этом является недостаточным. Использование же обработки в частотной области хотя и достаточно развито, но требует значительных вычислительных затрат.
1.3 Перечень решаемых в работе задач Основная цель работы состоит в разработке принципиально нового подхода к обработке медицинских изображений (на примере изображений лёгких человека, полученных с помощью компьютерного рентгеновского томографа фирмы General Electric CT 9000 в условиях Донецкого областного клинического территориального медицинского объединения (ДОКТМО)). Поставленная цель достигается решением следующих конкретных задач : • первоначальная обработка изображения на основе использования дискретного преобразования Фурье в четырёхслойной • формирование множества информативных признаков для распознавания, которые должны быть инвариантными как к • определение оптимальных параметров нейронной сети и параметров обучающего алгоритма; • проведение корректного обучения нейронной сети. Объектом исследования является грудная клетка человека, в частности исследование проводится на основе снимков лёгких.
Рисунок 1.1 - Различные томограммы органов грудной клетки. Научная новизна работы состоит в усовершенствовании методов и алгоритмов обработки медицинских изображений при помощи такого метода искусственного интеллекта, как нейронная сеть. Практическая значимость заключается в том, что результатом работы является разработанная методика обработки реальных медицинских изображений, полученных в условиях Донецкого Диагностического Центра (ДОКТМО). 2. Теоретический анализ проблемы и его реализация Существующие методы цифровой обработки изображений с позиций использования вычислительных средств можно разделить на две категории - структурированные и неструктурированные методы. Структурированные методы – такие, которые построены на использовании крупных вычислительных (программных) блоков, оперирующих векторами отсчетов, а не отдельными отсчетами изображений. Cреда MATLAB позволяет реализовывать методы обработки изображений, оперирующие не только с векторами, но и с массивами отсчетов. Неструктурированные методы – те, которые нельзя представить более крупными стандартными блоками, чем обычные для существующих цифровых вычислительных машин арифметико-логические операции над отдельными отсчетами сигналов. Неструктурированные методы, как правило, возникают на начальной стадии поиска решения содержательных задач обработки изображений и по мере нахождения решения перерастают в структурированные. Структурирование методов обработки изображений – основа повышения их вычислительной эффективности, построения вычислительных машин обработки изображений и специального математического обеспечения таких машин. Рассмотрим класс структурированных нелинейных алгоритмов, которые осуществляют преобразование вида: где Фk(xk)– нелинейная функция, которая определяется некоторым подмножеством рангов и (или) порядковых статистик выборки, образованной отсчетами сигнала из некоторой окрестности данного элемента, в последовательности упорядоченных отсчетов сигнала. Поэтому класс алгоритмов называется ранговыми алгоритмами. Обозначим через S окрестность элемента изображения, (k,l) - заданное определенным образом множество, окружающее центральный элемент. М -окрестность - подмножество элементов S-окрестности. Варианты M - окрестностей могут быть самыми разнообразными. Приведем некоторые примеры:
Медиана элементов М -окрестности:
Приведенные статистики удобно искать по локальной гистограмме. Существующие рекурсивные алгоритмы позволяют быстро обрабатывать окрестности любых размеров. Преимуществом ранговых алгоритмов является их отличие от методов линейной фильтрации, они лишены такого характерного недостатка как пространственная инерционность, которая заключается в том, что при использовании линейных фильтров влияние отдельных деталей изображения проявляется на результирующем изображении на расстоянии порядка размеров апертуры фильтра. Это заметно в частности в размывании границ деталей при сглаживании изображений, в искажении формы деталей при их выделении из фона и т.п. На первый взгляд может показаться, что вследствие переупорядочивания данных в вариационный ряд ранговые алгоритмы не используют пространственных связей между элементами изображений, и это является принципиальным недостатком. Действительно, ранговые алгоритмы инвариантны к пространственным связям и даже к размерности сигнала. Однако, как ни удивительно, это свойство является не недостатком, а преимуществом ранговых алгоритмов , еще одной стороной их адаптивного характера. Пространственные связи между элементами изображения, определяемые, например, принадлежностью их к одной детали, проявляют себя в вариационном ряду через параметры условной гистограммы распределения значений сигнала в окрестности данного элемента. В последнее время появилось много публикаций, в которых рассматриваются алгоритмы, основанные на вычислении линейной комбинации порядковых статистик, взятых с заранее подобранными из тех или иных соображений весами. Ранговые алгоритмы могут использоваться во всех процедурах обработки изображений – стандартизации, сглаживания, усиления детальности, выделения объектов из фоновой части, выделения границ, определения статистических характеристик и т.д. Ранговые алгоритмы локально-адаптивны по своей сути, поскольку их параметры являются функциями локальной характеристики изображений - локальной гистограммы. Термин "ранговые алгоритмы" в обработке изображений появился относительно недавно, когда множество алгоритмов, которые фактически относятся к классу ранговых, были уже достаточно известны. Для фильтрации импульсных помех и сглаживания изображений давно используется предложенный Тьюки алгоритм медианной фильтрации. Известны также алгоритмы экстремальной фильтрации, которые используют значения минимума и максимума в окрестности. Все эти алгоритмы можно рассматривать как частные случаи широкого класса ранговых алгоритмов. Методы ранговых преобразований позволяют осуществить нелинейное усиление высокочастотной составляющей изображения. Это приводит к повышению детальности изображений, однако сопровождается уменьшением контрастности тонкоструктурных объектов. Возможным вариантом устранения этого недостатка является использование взвешенных ранговых преобразований. Кроме применений для сглаживания, усиления детальности, выделения деталей изображений и границ деталей, ранговые алгоритмы можно употреблять для решения многих других задач обработки изображений, в частности, для диагностики статистических характеристик искажений видеосигнала, стандартизации изображений, определения статистических характеристик видеосигнала и измерения текстурных признаков. Применимость ранговых алгоритмов для кодирования связана с возможностями адаптивного квантирования мод при пофрагментной (не скользящей) обработке. В пакете IPT предложены некоторые функции ранговой обработки изображений. Функция D=ordfilt2(S, order, domain) позволяет пикселю изображения D, соответствующему центральному элементу маски, присвоить значение с номером order в отсортированном (по возрастанию) множестве. Функция D=ordfilt2(S, order, domain, А) работает аналогично функции D=ordfilt2(S, order, domain), за исключением того, что перед сортировкой к значениям пикселей, соответствующих ненулевым элементам маски фильтра domain, прибавляются значения из матрицы А. Частным случаем ранговой фильтрации является медианная фильтрация. Анализ и сравнение приведенных выше теоретических основ ранговых методов и функций пакета обработки изображений в системе MATLAB приводит к выводу о необходимости создания программных средств, реализующих методы ранговой обработки изображений. Такие работы проводятся. Они позволяют не только исследовать существующие алгоритмы, но и, выявив их недостатки, создавать новые высокоэффективные методы ранговой обработки изображений. Психофизические эксперименты показывают, что фотографическое или телевизионное изображение с подчеркнутыми границами часто воспринимается субъективно лучше, чем фотометрически совершенная продукция. Процедуру подчеркивания границ реализуют с использованием методов нечеткого маскирования ( разностных методов ). Суть этих методов состоит в следующем. Исходное изображение сканируют двумя апертурами с различной разрешающей способностью. В одной апертуре разрешающая способность отвечает норме, а во второй - ниже нормы. В результате образуются два массива: массив элементов изображения L и массив элементов нечеткого изображения
где k - коэффициент пропорциональности (в большинстве случаев - 3/5<k<5/6). Более распространенным вариантом этого метода является выражение:
где k - коэффициент усиления контрастности;
c - константа (часто c=128). В зависимости от размеров апертуры скользящего окна результат действия разностных методов находится в пределах от локального усиления контуров до выравнивания общего фона на изображении. В пространственной области усиление высоких частот осуществляет также алгоритм, представленный формулой:
где S - заданная окрестность элемента ( i, j ) изображения, которая окружает центральный элемент с координатами ( i, j ), включая его самого; Это среднеарифметическое значение элементов S-окрестности, которая состоит из m*n элементов. Недостатком метода нечеткого маскирования, представленного выражением (2.8), является то, что коэффициент усиления k - константа. Это приводит к одинаковому усилению слабоконтрастных участков и участков с достаточным контрастом. Предложено также адаптивное определение коэффициента усиления k=K(i,j):
а параметр c- "желательное", изначально заданное значение среднего (корректирующие слагаемое). Однако этот метод имеет недостаток : рядом с усилением мелких деталей изображения, он искажает участки с одинаковыми уровнями яркостей. Предложен также метод, который позволяет формировать коэффициент усиления адаптивно относительно локальных участков изображения. Предложенный алгоритм усиления локальных контрастов обобщает рассмотренный выше метод (2.8) и представляется следующим выражением:
Q - нормирующий множитель, 0<Q<=1; Lo - среднее значение яркости всего изображения размером I*J элементов
Существуют другие, более сложные модификации метода нечеткого маскирования. К таким методам можно отнести методы коррекции фоновой составляющей, на которую накладывается высокочастотная текстура объектов и деталей изображения. Использование этого подхода приводит к усилению локальных контрастов деталей различных размеров и улучшению визуального восприятия изображений. Известны также методы представления детальной составляющей изображения через локальный контраст. Они позволяют создавать новые классы методов нечеткого маскирования, базирующиеся на нелинейных преобразованиях локальных контрастов. Это в свою очередь говорит об общности различных методов преобразования контрастности изображений. 2.1.3 Методы гистограмных преобразований Гистограмма распределения яркостей реального изображения, подвергнутого линейному квантированию, имеет ярко выраженный подъем в сторону малых уровней. Поэтому мелкие детали на темных участках видимы плохо, а сами изображения характеризуются низким контрастом. С целью повышения контраста таких изображений используют методы видоизменения гистограммы. Суть этих методов состоит в преобразовании яркостей исходного изображения таким образом, чтобы гистограмма распределения яркостей приобрела желательную форму. Оптимальным с точки зрения зрительного восприятия человеком является изображение, элементы которого имеют равномерное распределение яркостей. Множество исследователей получили ряд улучшенных изображений путем выравнивания гистограммы, то есть в каждом случае они стремились достичь равномерности распределения яркостей обработанного изображения. У. Фрэй исследовал метод видоизменения гистограмм, который обеспечивал экспоненциальную или гиперболическую форму распределения яркостей улучшенного изображения. Д. Кетчам усовершенствовал этот метод, применив скользящую "локальную" гистограмму, полученную для некоторого участка изображения. Процедура выравнивания гистограммы состоит из следующих действий:
Это преобразование эффективно для улучшения визуального качества низко контрастных деталей. Существует также ряд известных методов видоизменения гистограммы, которые приводят к получению изображений с заранее заданным распределением. Описанные методы преобразования гистограммы могут быть глобальными, то есть использовать информацию обо всем изображении, и скользящими, когда для преобразования используются локальные области изображения. Рассмотренные выше подходы служат основой широкого класса гистограммных методов преобразования изображений. Благодаря своей высокой эффективности методы гистограммных преобразований нашли широкое применение при решении задач обработки изображений. Этим объясняется существование большого количества методов класса гистограммных преобразований, что позволяет решать широкий круг задач с учетом разнообразных нюансов. Методы данного класса бывают глобальными и локальными (или еще их называют скользящими). Глобальные методы гистограммных преобразований являются, в сущности, табличными методами. Поэтому основное их преимущество состоит в быстродействии . Однако, глобальные методы не используют при преобразовании характеристик локальных областей изображения, поэтому они не обеспечивают эффективную обработку тонкоструктурных областей. Для более детальной обработки изображений используют скользящие методы. Они обеспечивают качественное контрастирование мелких деталей изображения. Вместе с тем, они более объемны по вычислительным затратам. Поэтому при использовании методов класса гистограммных преобразований нужно искать компромисс между качеством и быстродействием обработки изображений. Основным этапом при создании методов гистограммных преобразований является корректное построение гистограммы распределения яркостей элементов изображения. Для этого в большинстве случаев используются встроенные функции hist, imhist. В Matlab V.4.x функция построения гистограммы яркостей элементов изображения работает некорректно, однако этот недостаток устранен в последующих версиях.
2.1.4 Метод преобразования локальных контрастов Существуют различные подходы к визуализации. Одним из существенных недостатков этих методов является то, что в большинстве своем они обеспечивают формирование слабоконтрастных изображений. Это вызывает необходимость развития методов их обработки. Поэтому основная цель методов улучшения состоит в преобразовании изображений к более контрастному и информативному виду. Довольно часто на изображении присутствуют искажения в определенных локальных областях, которые вызваны дифракцией света, недостатками оптических систем или расфокусировкой. Это порождает необходимость выполнения локальных преобразований изображения. Рассмотрим известную технологию повышения качества изображений, которая основывается на преобразовании локальных контрастов. Основная ее идея состоит в том, что для каждого элемента изображения сначала определяется локальный контраст, а потом происходит его нелинейное усиление и восстановление яркости данного элемента изображения из уже скорректированного локального контраста. Основные шаги реализации метода представлены на рис. 2.1 в виде структурной схемы. Рисунок 2.1 - Структурная схема метода усиления локальных контрастов. На первом этапе выбирается элемент L( i, j ) с координатами (i, j) исходного изображения L,
а m=3n, n>1.Области W1 и W2 представляют собою скользящие окна в виде квадрата с центром в элементе с координатами (i,j). Скользящее окно W1 размещено внутри скользящего окна W2. Следует отметить, что форма и размеры скользящего окна, в общем случае, могут быть произвольными. В большинстве методов размеры апертуры остаются постоянными на протяжении реализации всего метода. Однако существуют методы обработки изображений с адаптивным скользящим окном. Известно, что степень обработки сигналов зависит от размеров апертуры фильтра, а именно при малом размере апертуры фильтра операции усреднения подвергается меньшее число значений, что обеспечивает лучшее сохранение контрастных деталей сигнала. Но при этом шум будет сглажен хуже. И наоборот, при большом размере апертуры фильтра сглаживание шума будет происходить лучше, но при этом возможна "потеря" некоторых контрастных деталей, присутствующих в исходном сигнале. Итак, становится ясным, что качество обработки изображения можно улучшить путем выбора наиболее подходящих размеров апертуры. К сожалению, реальные изображения не являются стационарными: они содержат как монотонные области, так и изображения перепада, поэтому на практике очень трудно подобрать оптимальные размеры апертуры фильтра. В подобных ситуациях качество обработки можно улучшить, если использовать апертуру с большими размерами в монотонных областях обрабатываемого изображения и апертуру с малыми размерами вблизи областей перепада. Третий этап рассматриваемого метода состоит в нелинейном усилении локального контраста
Функция На четвертом этапе происходит восстановление элемента изображения с координатами (i, j) и скорректированного контрастом
Расчет с помощью выражений (2.17) - (2.22) проводят для каждого элемента изображения L. Экспериментальные исследования и компьютерное моделирование данного метода показали его недостаточную эффективность , поскольку при таком подходе результирующее изображение получается размытым . Для устранения этого недостатка предложено использовать вместо усредненного значения
Рассмотренный метод является классическим примером методов класса преобразования локальных контрастов. Эти методы позволяют решать задачи не только улучшения визуального качества изображений, но и реализовывать как высокочастотную, так и низкочастотную фильтрацию с помощью применения различных функций преобразования. 2.2 Постановка задачи и её реализация В своей магистерской работе я буду ориентироваться на язык программирования Matlab , в частности на пакет Image Processing Toolbox . Этот пакет владеет мощными средствами для обработки изображений. Система MATLAB и пакет прикладных програм Image Processing Toolbox (IPT) является хорошим инструментом разработки, исследования и моделирования методов и алгоритмов обработки изображений. При решении задач обработки изображений этот пакет позволяет идти двумя путями. Первый из них состоит в самостоятельной программной реализации методов и алгоритмов. Другой путь позволяет моделировать решение задачи с помощью готовых функций, которые реализуют наиболее известные методы и алгоритмы обработки изображений. И тот, и другой способ оправдан. Но все же для исследователей и разработчиков методов и алгоритмов обработки изображений предпочтительным является второй путь. В том и другом подходе объектом исследования является изображение. Я буду ориентироваться на растровые изображения, которые представляют собой двумерный массив, элементы которого (пикселы) содержат информацию о цвете. В дальнейшем, при рассмотрении методов обработки изображений, будем считать, что изображение представляется матрицей чисел (размер матрицы N*M), где значение каждого элемента отвечает определенному уровню квантования его энергетической характеристики (яркости). Это так называемая пиксельная система координат . Она применяется в большинстве функций пакета IPT. Обработка изображений осуществляется рекурсивными и нерекурсивными методами. Рекурсивные методы используют результат обработки предыдущего пиксела, нерекурсивные - не используют. В большинстве случаев используются нерекурсивные алгоритмы обработки изображений. Обработка изображений является многоплановой задачей. Сюда включают решение задач фильтрации шумов, геометрической коррекции, градационной коррекции, усиления локальных контрастов, резкости, восстановления изображений и др. Одним из подходов к обработке изображения с целью улучшения его визуального качества является непосредственное использование разных фильтров. В зависимости от спецификации шумов могут применяться различные способы фильтрации: фильтры на основе преобразования Гаусса (которые используются обычно в тех случаях, когда необходимо уменьшить паразитные сигналы), полосовые фильтры с ограниченным носителем (которые предназначены для отфильтровывания верхних частот и применяются совместно с методами выделения краев изображения в задаче поиска полезной информации). Известны также алгоритмы линейной низкочастотной фильтрации, например, фильтрация скользящим средним, экспоненциальная и медианная фильтрация. Однако данные фильтры плохо подавляют мелкие, но контрастные образования, а также смазывает границу – расширяет полосу граничных точек в задаче сегментации. В своей магистерской работе я собираюсь использовать принципиально новый подход к фильтрации, а именно применять перспективный метод нелинейной низкочастотной фильтрации с использованием нейроподобной структуры на основе преобразования Фурье. Рассматриваемый фильтр основан на четырехслойной НС прямого распространения (рисунок 2.2). Рисунок 2.2 - Четырёхслойная НС прямого распространения. На входы НС подаются сигналы Х1 ,.. . , Х n с помехами. На выходе формируется отклик У1, ..., Yn без помех. Процедура фильтрации заключается в следующем. На первый слой сети поступают значения сигнала. На втором слое сети осуществляется дискретное преобразование Фурье (ПФ), в результате которого каждому нейрону второго слоя соответствует линия частотного спектра (рисунок 2.3). Рисунок 2.3 - График 4-хслойной НС прямого распространения. На следующем слое сети происходит непосредственно фильтрация в частотной области. Посредством синаптических весов на следующий слой формируются сигналы только тех нейронов, которые входят в полосу пропускания рассматриваемого фильтра. На посл еднем слое осуществляется обратное ПФ, которое превращает спектр в отфильтрованный сигнал. На выходе НС формируется обработанный сигнал. Путем настройки третьего слоя можно гибко менять параметры фильтра, что позволит осуществлять кроме высокочастотной фильтрации уточнение границ, контрастирование, удаление мелких локальных образований, выравнивание освещенности. С помощью спектрального анализа исходного изображения можно выявить особенности шумов и искажений, а значит, выработать и способ борьбы с ними. Преобразование Фурье действительной функции s(x) , заданной в пределах х от минус бесконечности до бесконечности, является комплексной величиной:
Полагая, что составляющие спектра S(u) существуют на частотах u в интервале от минус бесконечности до бесконечности, можно определить обратное преобразование Фурье по формуле:
Из формулы (2.25) очевидно, что спектр действительного сигнала s(x) есть:
Sc(u), Ss(u) - действительная и мнимая части спектра. При компьютерной обработке последовательности отсчётов сигнала интегральн ы е соотношения заменяют соответствующими операциями дискретного суммирования. Очевидно, что для цифрового сигнала ПФ в общем случае не может быть реализовано из-за необходимости суммирования безконечного числа членов. Компьютерные алгоритмы ПФ дискретной последовательности отсчётов s(p) , имеющей конечную длину 0<=p<=N-1 , сводятся к вычислению конечного числа коэффициентов S(q), 0<=q<=Q-1 , согласно соотношению:
Формула (2.30) представляет собой дискретную аппроксимацию преобразования (2.25), при которой функция s(x) заменяется ступенчатой функцией s(p)=s(хp) в пределах протяжённости элемента дискретизации, где: x p =pdx (dx – шаг дискретизации ). Выражение (2.30) есть приближение, качество которого должно улучшаться при увеличении N и соответствующем уменьшении шага дискретизации dx . В работе я также планирую заняться распознаванием двумерных контрастных изображений объектов по инвариантным информативным признакам, для реализации чего мною намечено в частности решение 3-ёх задач: 1. Формирование множества информативных признаков для распознавания, которые должны быть инвариантными как к смещению фигур в плоскости, так и к их поворотам. 2. Определение параметров НС, параметров обучающего алгоритма. 3. Проведение корректного обучения НС. Эффективность работы системы распознавания с выбранными параметрами будет оцениваться в результате цикла статических испытаний, по результатам которых будет приниматься решение о необходимости корректирования параметров системы. 3. Выводы по работе и перспективы исследований Результатом данной работы является обобщение и систематизация теоретических сведений о методах и алгоритмах обработки изображений. Был проведен научный поиск по теме "Разработка методов и алгоритмов обработки медицинских изображений с использованием методов искусственного интеллекта, проведен анализ существующих разработок в области использования нейронных сетей для этих целей, обоснована актуальность темы магистерской работы, определены направления исследования в данной области. Проанализировав существующие на сегодняшний день алгоритмы и методы обработки медицинских изображений, можно подвести итоги. Значительная часть задач обработки информации и анализа данных связана с изображениями. Примерами могут служить обработка и анализ данных дистанционного зондирования Земли со спутников, объемные изображения объектов, полученные с помощью голографических устройств, результаты применения методов неразрушающих исследований и контроля в промышленности, разработка “органов зрения” роботов и современных медицинских систем диагностики (рентгенография, машинная томография, эндоскопия и т.д.). Для успешного решения задач поиска и идентификации объектов, определения различного рода их количественных характеристик необходимо, чтобы первичные изображения характеризовались высоким визуальным качеством, которое теряется из-за неудовлетворительных условий получения изображений, несовершенства систем передачи видеоинформации и ее отображения, влияния помех и т.п. Поэтому актуальной является задача преобразования изображений с целью улучшения их визуального качества и повышения информативности. Все основное множество методов, которые решают эту задачу, делится на методы обработки в частотной и пространственной областях . Для обработки изображений в пространственной области наибольшее распространение получили методы пяти классов, которые были рассмотрены выше: 1) гистограммные методы; К преимуществам методов обработки изображений в пространственной области относится возможность быстрой обработки в масштабе реального времени телевизионного видеосигнала, а к недостаткам - ограниченность функциональных возможностей и недостаточная эффективность. При рассмотрении методов обработки изображений всегда остро стоит вопрос выбора критериев оценки качества их преобразования. Этот вопрос всегда был актуальным, однако ставился и решался он разными способами. Разделение на классы условно, поскольку все методы имеют в своей основе локальный контраст элементов изображения. Хотя способы обработки изображений в частотной области и достаточно развиты, но требуют значительных вычислительных затрат и для решения практических задач применяются реже. Надеюсь, что проделанная мною работа будет полезна и применима на практике.
|
|
 E-mail:
E-mail: 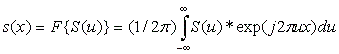 (2.26)
(2.26) 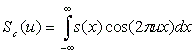 (2.28)
(2.28) 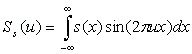
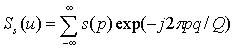 (2.30)
(2.30)