
Подсистема оптимизации материальных затрат и человеческих ресурсов крайне необходима в первую очередь для предприятий капиталоемких отраслей - топливно-энергетического комплекса, транспорта, добывающей и перерабатывающей промышленности, стройиндустрии, телекоммуникаций. Основная статья расходов у таких предприятий это, как правило, расходы на ремонтно-техническое обслуживание. Используемая в настоящее время в мировой практике стратегия ремонтно-технического обслуживания предполагает концентрацию ресурсов и усилий на профилактических ремонтах с учетом состояния оборудования. Широкое распространение получили лишь некоторые информационные системы, которые предназначены для автоматизации управления техобслуживанием и ремонтами оборудования предприятий. Это такие системы как: АСУ РТО (Украина), система SAP R3 - Германия, IFS - Швеция, M.I.S. (ANSALDO) – Италия. Основной задачей таких систем является:
• Планирование ремонтов оборудования, включающее:
- перспективное планирование;
- годовое планирование;
- планирование капитальных, средних, текущих ремонтов;
- месячное планирование;
• Организация технического обслуживания (ТО) оборудования;
• Планирование материальных ресурсов на ремонты оборудования и ТО;
• Контроль технического состояния оборудования;
• Текущее планирование ремонтных работ;
• Организация и контроль выполнения ремонтных работ;
• Оформление отчетной документации о проведенных ремонтах.
В 1998 году корпорация “Technology for Energy” провела анализ работы более чем 500 энергопредприятий США и Европы, который показал, что использование диагностического мониторинга в сочетании с АСУ РТО приводит к снижению затрат на ремонт оборудования до 50-80%, расходов на техническое сопровождение до 50-80%, объёмов материально-производственных запасов до 30% и повышению рентабельности производства до 20-60% [1]
Несмотря на все достоинства этих систем, ни в одной из них задачи оптимизации не решаются с помощью математических методов. На данный момент одна из таких систем внедрена на Киевской ТЭЦ-5 АЭК «Киевэнерго». По результатам работы АСУ РТО оценили полученный экономический эффект в размере 10-15%.
Исходя из анализа можно утверждать, что при условии использования математических методов для решения поставленной задачи материальные затраты и человеческие ресурсы можно существенно сократить и повысить процент экономического эффекта от внедрения таких информационных систем.

• анализ организации технического обслуживания и ремонта электротехнического оборудования предприятия;
• разработка концепции технического обслуживания и ремонта по объективному состоянию оборудования и методов оценки (идентификации) состояния;
• создание базы данных по используемому электрооборудованию с информацией, отражающей его техническое состояние (время выхода из строя электротехнического оборудования, время плановых ремонтов, периоды наработки на отказ, режимы эксплуатации, отказообразующие причины и т.п.);
• построение многомерной базы данных по технологии OLAP (Online Analytical Processing), где в качестве показателей фигурируют ключевые факторы, влияющие на работоспособность единиц электрооборудования
Разрабатываемая система будет использовать современные методы математического анализа факторов, влияющих на поддержание работоспособности электрооборудования, что позволит предупредить выход из строя рабочей единицы благодаря своевременным регламентным работам.
• разработка концепции системы сбора и обработки статистической информации о значениях показателей технического состояния объектов электроснабжения, а также данных о номенклатуре и количестве используемых запасных частей для изделия и его компонентов; эти данные извлекаются из специальных документов – формуляров изделия, его агрегатов и систем, в которых фиксируются результаты проведения операций технического обслуживания и ремонта, факты замены компонентов, календарные сроки выполнения операций (начало, конец), сведения о работниках, выполнявших операцию и т.д.;
• выполнение централизованного анализа накопленных эксплуатационных и логистических данных;
• проведение согласованной динамической корректировки планов технического обслуживания и ремонта, которая позволит уйти от выполнения регламентных работ по графику ППР и планировать и производить ремонты электрооборудования, исходя его фактического технического состояния;
• оптимизация затрат на ремонт и обеспечение заданного технического состояния электрооборудования при помощи математических методов.
Программа управления надежностью, основанная на CALS (Continuous Acquisition and Life cycle Support)-методологии, позволит повысить технико-экономические показатели системы электроснабжения за счет нахождения оптимального варианта системы с минимальными расчетными затратами. В основе CALS-технологий лежит минимизация затрат в ходе жизненного цикла объекта, повышение его качества и конкурентоспособности, при этом базовой является идея информационной интеграции стадий жизненного цикла электрооборудования.
Важными критериями оптимизации стоимости жизненного цикла объектов электроснабжения являются надежность и ремонтопригодность, а потому на следующем этапе «наполнения информацией» на основе предложенной технологии поддержки заданного технического состояния можно будет применить ряд соответствующих методик:
• анализ последствий возможных неисправностей и путей их предотвращения;
• сравнительный анализ эффективности методов организации обслуживания оборудования, позволяющих предотвратить возникновение неисправностей;
• анализ качества обслуживания объектов электроснабжения;
• разработка требований к вспомогательному оборудованию и подготовке персонала;
• формирование интегральных показателей (функционала), характеризующих эффективность системы.
Рассматривая проблему использования информации о техническом состоянии электротехнического оборудования для принятия решений по ремонтным воздействиям, целесообразно выделить три уровня адекватности оценок.
Первый уровень – идентификация технического состояния по показателям надежности, т.е. по параметру потока отказов или интенсивности восстановлений.
Второй уровень – идентификация технического состояния по вероятностным характеристикам дефектов и повреждений, выявленных в определенные моменты времени.
Третий уровень – идентификация состояния по непрерывно контролируемым технологическим параметрам, характеризующим техническое состояние элементов оборудования.
Реализация третьего уровня возможна лишь при условии наличия совершенных диагностических систем и адекватных математических моделей корреляционных связей между выходными параметрами и техническим состоянием оборудования. Второй уровень более доступен и требует достаточной информации по выявленным дефектам и повреждениям, а также моделей динамики их развития. Реализация первого уровня связана лишь с достаточностью статистического материала.
Корректность принятия решения о введении того или иного регламента технического обслуживания и ремонта зависит от технического состояния оборудования. Регламент технического обслуживания и ремонта как система правил, определяющих технологию, средства, объем, методы и периодичность ремонтных воздействий, зависит не только от технического состояния рассматриваемого оборудования. На него оказывает влияние структурная значимость данного оборудования в объемлющей технической системе и конкретные условия ее функционирования (в том числе чисто ремонтного характера, например, оснащенность ремонтной базы, наличие ресурсов и др.).
Перечисленные выше три уровня идентификации технического состояния, по сути, являются тремя уровнями оценки функции надежности. Первый уровень соответствует нулевому приближению, когда априорная информация отсутствует. Второй уровень соответствует случаю, когда задан априорный случайный процесс накопления повреждений данного типа. Третий уровень относится к случаю, когда прогноз осуществляется для каждой отдельно взятой реализации случайного процесса развития отказа. Использование того или иного уровня определяется необходимостью точностью прогноза и наличием соответствующих технических средств, программного и информационного обеспечения.
В общем виде задача определения времени вывода в ремонт обследуемого оборудования промышленного предприятия включает в себя следующие стадии:
• определение состава выводимого в ремонт оборудования с учетом технологических взаимосвязей;
• определение внешних (системных) ограничений;
• определение потребности конкретного оборудования в объеме и сроке ремонта;
• определение внутренних ограничений по срокам и затратам (включая все виды обеспечения ремонта);
• согласование внешних и внутренних ограничений;
• подготовка графика вывода в ремонт, включающего в себя сроки остановов и их продолжительность.
Сущность этой задачи состоит в определении ремонтных программ оборудования с одновременным использованием нормативной базы и результатов оценок технического состояния. Такое сочетание информации позволяет наиболее полно использовать любую информацию о техническом состоянии оборудования, получаемую как с помощью систем диагностики, так и по экспертным оценкам.
Под ремонтными программами подразумеваются графики и сроки выполнения конкретных наборов ремонтных работ, наиболее полно отражающих динамику изменения технического состояния оборудования.
Диагностическими параметрами могут быть:
• наработки до отказа, времена восстановлений, законы распределений;
• наработки до появления повреждения, времена восстановления, законы распределения времени появления повреждения;
• модели развития повреждения, стохастические характеристики развития повреждения, предельно допустимые уровни повреждения.
Общим критерием оптимальности при решении задачи планирования ремонтов основного заводского электрооборудования является минимум затрат, включающих затраты на выполнение ремонтных работ, а также ущерб от возможных аварийных ситуаций. В существующих условиях основным критерием оптимальности планирования ремонтов является максимальное заполнение так называемой ремонтной площадки, т.е. наиболее эффективное использование ремонтного резерва предприятия.
При такой постановке весь парк электрооборудования разбивается на ремонтные элементы Пi. Наименьшим наблюдаемым ремонтным элементом может быть единица оборудования или его составная часть. Элементы Пi могут быть сгруппированы по признакам принадлежности к одной технологической системе, технологическому комплексу (например, котельная установка, турбинная установка и т.д.), по функциональному назначению (например, группы насосов, электродвигателей), конструктивно-компоновочным особенностям или принадлежности к одному заводу-изготовителю. Такие группировки необходимы для решения задач подготовки ремонта, оценки надежности и др. Таким образом формируются пересекающиеся множества {Пi}.
Множества являются пересекающимися, так как одни и те же элементы (единицы оборудования) могут попасть в различные подмножества в зависимости от горизонта планирования и существа решаемой задачи (например, планирование потребности в запасных частях и материалах может производиться для схемы планирования трудозатрат как по иерархической соподчиненности ремонтных элементов, так и с группированием оборудования по типам, заводам-изготовителям и другим группировкам).
Каждый ремонтный элемент Пi характеризуется своей ремонтной программой Ri – определенной временной и количественной закономерностью выполнения ремонтных воздействий. При этом ремонтная программа отражает реальное техническое состояние элемента и может изменяться во времени:
Ri(t)=f(технического состояния Пi)=f(tэкс), (1)
где tэкс – длительность эксплуатации элемента.
Каждому ремонтному элементу придается его адрес (наименование, условия входимости в другие элементы) и массив информации, определяемой существом задачи (например, для задачи планирования материалов – перечень и расход материалов).
Решение задачи оптимизации и планирования объемов ремонтных работ сводится к определению базовых точек последнего выполнения известных ремонтных воздействий нормального и переменного объемов и определению состава работ, попадающих в планируемый период. Информационная модель энергосистемы предприятия для данной задачи представляется конечным связным графом. Вершины графа представляют собой адреса ремонтных элементов, а ребра характеризуют условия входимости.
Если нет математических зависимостей, характеризующих интенсивность исчерпания ресурса, то решение принимается на уровне управления по экспертным оценкам фактического состояния оборудования и возможности выполнения работы в ближайший или последующий интервалы планирования.
В любом случае базовой точкой будет считаться факт последнего выполнения данной работы. Если ресурс ремонтного элемента значительно превосходит длительность ремонтного цикла (в 2раза и более) и соизмерим с жизненным циклом изделия, работы переводятся в разряд разовых, вероятность повторения которых мала (близка к нулю).
Если имеются результаты диагностики технического состояния и известны математические зависимости изменения во времени ресурсов элементов, дата их выполнения устанавливается с учетом предполагаемой ситуации в системе технического обслуживания и ремонта. За базовую точку принимается либо начало эксплуатации оборудования (начало новой стадии жизненного цикла после выполнения в ремонтном цикле последнего ремонта), либо дата последнего выполнения данной работы.
После того как сформирован объем ремонтных работ, рассчитываются все виды затрат с использованием нормативной базы. Материальные и трудовые затраты могут быть сгруппированы по различным признакам в зависимости от интересов конкретного пользователя. Таким образом, потребность оборудования в ремонтных воздействиях рассчитывается и уточняется с учетом любых сведений, дополняющих нормативную базу и характеризующих реальное техническое состояние.
Процесс управления предприятием представляет собой непрерывную разработку управленческих решений и применение их на практике. От эффективности разработки этих решений в значительной степени зависит успех дела. И прежде чем начинать какое-либо дело, необходимо определить цель своих действий. В процессе производства очень часто приходится сталкиваться с критическими проблемами, и от того, на сколько оптимально принятое решение, будет зависеть конечный финансовый результат деятельности предприятия. Потребность в решении возникает только при наличии проблемы, которая в общем, виде характеризуется двумя состояниями - заданным (желаемым) и фактическим (прогнозируемым), и именно прогнозирование будет отправной точкой в процессе принятия управленческого решения. Рассогласование между этими состояниями предопределяет необходимость выработки – управленческого решения и контроля за его реализацией. Чтобы прогнозирование было наиболее эффективным, цели должны быть конкретными и измеримыми. То есть для каждой цели должны существовать критерии, которые позволили бы оценить степень достижения цели. Без этих критериев не возможна реализация одной из основных функций управления - контроля. Исходя из этого, можно сделать вывод, что цель, степень достижения которой можно количественно измерить, будет всегда лучше цели, сформулированной лишь словесно. Прогнозирование - это своего рода умение предвидеть, анализ ситуации и ожидаемого хода её и изменения в будущем. Так как каждое решение - это проекция в будущее, а будущее - содержит элемент неопределенности, то важно правильно определить степень рисков, с которыми сопряжена реализация принятых решений. Метод прогнозирования – это способ исследования объекта прогнозирования, направленный на разработку прогноза. Совокупность специальных правил, приемов и методов составляет методику прогнозирования. Наибольшее распространение получил эффективный алгоритм обучения нейронных сетей и несколько общепризнанных методов прогнозирования временных рядов:
• Методы Бокса-Дженкинса (ARIMA, ARMA)
• Регрессионные
• Эконометрические
В настоящее время, на мой взгляд, самым перспективным количественным методом прогнозирования является использование нейронных сетей. Можно назвать много преимуществ нейронных сетей над остальными алгоритмами, ниже приведены два основных.
При использовании нейронных сетей легко исследовать зависимость прогнозируемой величины от независимых переменных. Например, есть предположение, что поломки на следующей неделе каким-то образом зависят от следующих параметров:
• поломки в последнюю неделю
• поломки в предпоследнюю неделю
• поломки в предпоследнюю неделю
• количества неполадок (отключений)
Хотелось бы построить систему, которая бы все это естественным образом учитывала и строила бы прогнозы.
В такой постановке задачи большая часть классических методов прогнозирования будет просто несостоятельной. Можно попробовать построить систему на основе нелинейной множественной регрессии, или вариации сезонного алгоритма ARIMA, позволяющей учитывать внешние параметры, но это будут модели скорее всего малоэффективные (за счет субъективного выбора модели) и крайне негибкие.
Используя же даже самую простую нейросетевую архитектуру (персептрон с одним скрытым слоем) и базу данных (с поломками и всеми параметрами) легко получить работающую систему прогнозирования. Причем учет, или не учет системой внешних параметров будет определяться включением, или исключением соответствующего входа в нейронную сеть.
Более искушенный эксперт может с самого начала воспользоваться каким-либо алгоритмом определения важности (например, используя Нейронную сеть с общей регрессией и генетической подстройкой) и сразу определить значимость входных переменных, чтобы потом исключить из рассмотрения мало влияющие параметры.
Еще одно серьезное преимущество нейронных сетей состоит в том, что эксперт не является заложником выбора математической модели поведения временного ряда. Построение нейросетевой модели происходит адаптивно во время обучения, без участия эксперта. При этом нейронной сети предъявляются примеры из базы данных и она сама подстраивается под эти данные.
Недостатком нейронных сетей является их недетерминированность. Имеется в виду то, что после обучения имеется "черный ящик", который каким-то образом работает, но логика принятия решений нейросетью совершенно скрыта от эксперта. В принципе, существуют алгоритмы "извлечения знаний из нейронной сети", которые формализуют обученную нейронную сеть до списка логических правил, тем самым создавая на основе сети экспертную систему. К сожалению, эти алгоритмы не встраиваются в нейросетевые пакеты, к тому же наборы правил, которые генерируются такими алгоритмами достаточно объемные.
Рассмотрим, что представляет собой искусственная нейронная сеть и каковы принципы ее функционирования. Нейронная сеть, которая является основой работы самообучающихся нейропрограмм, представляет собой совокупность «нейронов» — простых элементов, связанных между собой определенным образом. «Нейроны» и межнейронные связи задаются при помощи программирования на обычном компьютере. Структура взаимосвязей между «нейронами» в нейрокомпьютере или нейропрограмме аналогична таковой в биологических объектах. Искусственный «нейрон» имеет коммуникации с другими «нейронами» через «синапсы», передающие сигналы от других «нейронов» к данному («дендриты») или от данного «нейрона» к другим («аксон»). Несколько «нейронов», связанных между собой определенным образом, и образуют нейронную сеть.
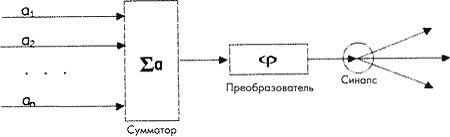
Рисунок 1 Формальный «нейрон»
На рисунке 1 представлен «нейрон» с группой «синапсов». «Нейрон» состоит из двух функциональных блоков: входного сумматора и собственно «нейрона», или преобразователя. Функционирование «нейрона» происходит следующим образом. В текущий момент времени через входные «синапсы» (на рисунке их 3) на «нейрон» направляются сигналы от других «нейронов» и/или из внешнего мира.
Каждый «синапс» имеет параметр, называемый весом «синапса» и представляющий какое-либо число. Сигнал, проходящий через «синапс», умножается на вес этого «синапса». в зависимости от веса сигнал может быть усилен (модуль веса >1) или ослаблен (модуль веса <1) по амплитуде. Сигналы от всех «синапсов», ведущих к данному нейрону, принимает сумматор.
Сумматор производит суммирование всех пришедших сигналов и подает на преобразователь одно число — полученную сумму. Величина этого числа будет зависеть как от величин исходных сигналов, так и от весов «синапсов». «Нейрон», получивший это число, преобразует его согласно своей функции, в результате которой получается другое число, и отправляет его по «аксону» всем остальным «нейронам» через соответствующие «синапсы». Последующие «нейроны» производят с полученными сигналами такие же операции, лишь с тем различием, что, во-первых, веса их «синапсов» могут быть уже другими, во-вторых, другие «нейроны» могут иметь другой вид функции преобразования. Эта функция, называемая характеристической, имеет вид 2:
f(X)=X/(C+TXT), (2)
где Х — сигнал, поступаемый с сумматора, С — константа, называемая характеристикой «нейрона». Экспериментальным путем получено, что оптимальный диапазон характеристики для решения подаляющего большинства задач составляет от 0,1 до 0,8 (рисунок 2).
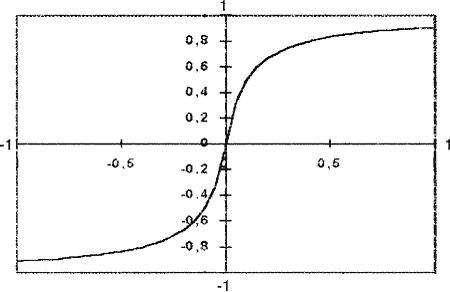
Рисунок 2 График характеристической функции.
Выбор функции такого вида обусловлен ее гладкостью, непрерывностью на всем диапазоне переменных значений Х, диапазон значений всегда ограничен.
В случае эмуляции нейросети на обычном компьютере все математические операции осуществляет программа. Таким образом, нейронная сеть, получающая на входе некоторый сигнал, способна после прохода его по «нейронам» выдавать на выходе определенный ответ, который зависит от весовых коэффициентов всех «нейронов» и от самого сигнала.
При создании новой нейросети в памяти компьютера отводится место под массив синаптических весов, называемый картой. Этот массив заполняется совершенно случайными числами из определенного диапазона. Поэтому каждая созданная сеть даже при одних и тех же параметрах (число нейронов, их характеристика) является уникальной. Уникальность сетей проявляется в том, что сети с одинаковыми параметрами, обучающиеся на одинаковых задачах, ведут себя неодинаково. Это касается времени обучения, качества обучения, уверенности в выдаваемых ответах при тестировании. В этом еще одно сходство сетей с биообъектами.
Рассмотрим работу сети безотносительно к процессу обучения или выдачи решения. После инициализации сети веса всех синапсов случайны. В начальный момент времени на входные нейроны через входные синапсы (один или несколько) подается из внешнего мира вектор входных сигналов, представляющий набор чисел (или одно число). Далее этот сигнал начинает распространяться по всем связям между нейронами, изменяясь при прохождении через каждый нейрон согласно схеме функционирования нейрона. В конечном итоге, после одного прохода выходные нейроны выдадут во внешний мир какие-либо сигналы. Вся процедура однократного прохождения сигналов по нейронной сети является тактом функционирования сети. Можно не считывать сигналы с выходных нейронов после одного такта функционирования, а продолжить обмен сигналами еще несколько раз, не подавая сигналов на вход. Обычно количество тактов функционирования между подачей сигналов на вход и снятием сигналов с выхода фиксировано для данной сети. Как правило, этот параметр задается при инициализации сети и хранится в файле сети вместе с матрицей коэффициентов (как и некоторые другие параметры - число нейронов, характеристика нейронов и т.д.).
Таким образом, нейронная сеть, получающая на входе некоторый сигнал, способна после прохода его по нейронам выдавать на выходе определенный ответ, который зависит от весовых коэффициентов всех нейронов и от самого сигнала. Очевидно, что при осуществлении таких процедур на только что инициализированной сети мы будем получать на выходе сигналы, лишенные всякого смысла (весовые коэффициенты случайны). Чтобы добиться выдачи сетью требуемого результата, необходимо обучить ее.
Если задача будет решаться с помощью нейронной сети, то необходимо собрать данные для обучения. Обучающий набор данных представляет собой набор наблюдений, для которых указаны значения входных и выходных переменных. Первый вопрос, который нужно решить, - какие переменные использовать и сколько (и каких) наблюдений собрать.
Выбор переменных (по крайней мере первоначальный) осуществляется интуитивно. Опыт работы в данной предметной области поможет определить, какие переменные являются важными. Для начала имеет смысл включить все переменные, которые, могут влиять на результат - на последующих этапах это множество сокращается.
Нейронные сети могут работать с числовыми данными, лежащими в определенном ограниченном диапазоне. Это создает проблемы в случаях, когда данные имеют нестандартный масштаб, когда в них имеются пропущенные значения, и когда данные являются нечисловыми.
Более трудной задачей является работа с данными нечислового характера. Чаще всего нечисловые данные бывают представлены в виде номинальных переменных типа Пол = {Муж , Жен }. Однако, нейронные сети не дают хороших результатов при работе с номинальными переменными, которые могут принимать много разных значений.
Нечисловые данные таких типов можно либо преобразовать в числовую форму, либо объявить незначащими. Значения дат и времени, если они нужны, можно преобразовать в числовые, вычитая из них начальную дату (время). Обозначения денежных сумм преобразовать совсем несложно. С произвольными текстовыми полями (например, фамилиями людей) работать нельзя и их нужно сделать незначащими.
Вопрос о том, сколько наблюдений нужно иметь для обучения сети, часто оказывается непростым. Известен ряд эвристических правил, увязывающих число необходимых наблюдений с размерами сети (простейшее из них гласит, что число наблюдений должно быть в десять раз больше числа связей в сети). На самом деле это число зависит также от (заранее неизвестной) сложности того отображения, которое нейронная сеть стремится воспроизвести. С ростом количества переменных количество требуемых наблюдений растет нелинейно, так что уже при довольно небольшом (например, пятьдесят) числе переменных может потребоваться огромное число наблюдений. Эта трудность известна как "проклятие размерности", и мы обсудим ее дальше в этой главе.
Для большинства реальных задач бывает достаточно нескольких сотен или тысяч наблюдений. Для особо сложных задач может потребоваться еще большее количество, однако очень редко может встретиться (даже тривиальная) задача, где хватило бы менее сотни наблюдений. Если данных меньше, то на самом деле просто недостаточно информации для обучения сети, и лучшее, что можно сделать - это попробовать подогнать к данным некоторую линейную модель.
При создании так называемых "наивных" моделей предполагается, что некоторый последний период прогнозируемого временного ряда лучше всего описывает будущее этого прогнозируемого ряда, поэтому в этих моделях прогноз, как правило, является очень простой функцией от значений прогнозируемой переменной в недалеком прошлом.
Самой простой моделью является: Y(t+1)=Y(t), что соответствует предположению, что "завтра будет как сегодня".
Вне всякого сомнения, от такой примитивной модели не стоит ждать большой точности. Она не только не учитывает механизмы, определяющие прогнозируемые данные (этот серьезный недостаток вообще свойственен многим статистическим методам прогнозирования), но и не защищена от случайных флуктуаций, она не учитывает сезонные колебания и тренды. Впрочем, можно строить "наивные" модели несколько по-другому:
Y(t+1)=Y(t)+[Y(t)-Y(t-1)], (3)
Y(t+1)=Y(t)*[Y(t)/Y(t-1)], (4)
такими способами мы пытаемся приспособить модель к возможным трендам
Y(t+1)=Y(t-s), (5)
это попытка учесть сезонные колебания.
Члены временного ряда не являются статистически независимыми и не являются одинаково распределенными. Это значит, что нельзя распространять свойства и правила статистического анализа случайной выборки на временные ряды. С другой стороны, взаимозависимость членов временного ряда создает свою специфическую базу для построения прогнозных значений анализируемого показателя.
Методы Бокса-Дженкинса (ARIMA)
В середине 90-х годов прошлого века был разработан принципиально новый и достаточно мощный класс алгоритмов для прогнозирования временных рядов. Большую часть работы по исследованию методологии и проверке моделей была проведена двумя статистиками, Г.Е.П. Боксом (G.E.P. Box) и Г.М. Дженкинсом (G.M. Jenkins). С тех пор построение подобных моделей и получение на их основе прогнозов иногда называться методами Бокса-Дженкинса. Алгоритм ARIMA встроен практически в любой специализированный пакет для прогнозирования. В классическом варианте ARIMA не используются независимые переменные. Модели опираются только на информацию, содержащуюся в предыстории прогнозируемых рядов, что ограничивает возможности алгоритма. В настоящее время в научной литературе часто упоминаются варианты моделей ARIMA, позволяющие учитывать независимые переменные. В данном учебнике мы их рассматривать не будем, ограничившись только общеизвестным классическим вариантом. В отличие от рассмотренных ранее методик прогнозирования временных рядов, в методологии ARIMA не предполагается какой-либо четкой модели для прогнозирования данной временной серии. Задается лишь общий класс моделей, описывающих временной ряд и позволяющих как-то выражать текущее значение переменной через ее предыдущие значения. Затем алгоритм, подстраивая внутренние параметры, сам выбирает наиболее подходящую модель прогнозирования. Как уже отмечалось выше, существует целая иерархия моделей Бокса-Дженкинса. Логически ее можно определить так
AR(p)+MA(q)->ARMA(p,q)->ARMA(p,q)(P,Q)->ARIMA(p,q,r)(P,Q,R)->... (6)
AR(p) -авторегрессионая модель порядка p.
Модель имеет вид:
Y(t)=f_0+f_1*Y(t-1)+f_2*Y(t-2)+...+f_p*Y(t-p)+E(t) (7)
гдеY(t)-зависимая переменная в момент времени t. f_0, f_1, f_2, ..., f_p - оцениваемые параметры. E(t) - ошибка от влияния переменных, которые не учитываются в данной модели. Задача заключается в том, чтобы определить f_0, f_1, f_2, ..., f_p. Их можно оценить различными способами. Правильнее всего искать их через систему уравнений Юла-Уолкера, для составления этой системы потребуется расчет значений автокорреляционной функции. Можно поступить более простым способом - посчитать их методом наименьших квадратов.
MA(q) -модель со скользящим средним порядка q.
Модель имеет вид:
Y(t)=m+e(t)-w_1*e(t-1)-w_2*e(t-2)-...-w_p*e(t-p) (8)
Где Y(t)-зависимая переменная в момент времени t. w_0, w_1, w_2, ..., w_p - оцениваемые параметры.
Регрессионные методы прогнозирования
Наряду с описанными выше методами, основанными на экспоненциальном сглаживании, уже достаточно долгое время для прогнозирования используются регрессионные алгоритмы. Коротко суть алгоритмов такого класса можно описать так.
Существует прогнозируемая переменная Y (зависимая переменная) и отобранный заранее комплект переменных, от которых она зависит - X1, X2, ..., XN (независимые переменные). Природа независимых переменных может быть различной. Например, если предположить, что Y - уровень спроса на некоторый продукт в следующем месяце, то независимыми переменными могут быть уровень спроса на этот же продукт в прошлый и позапрошлый месяцы, затраты на рекламу, уровень платежеспособности населения, экономическая обстановка, деятельность конкурентов и многое другое. Главное - уметь формализовать все внешние факторы, от которых может зависеть уровень спроса в числовую форму.
Модель множественной регрессии в общем случае описывается выражением
![]() (9)
(9)
В более простом варианте линейной регрессионной модели зависимость зависимой переменной от независимых имеет вид:
![]() (10)
(10)
Здесь
![]() подбираемые коэффициенты регрессии,
- компонента ошибки. Предполагается, что все ошибки независимы и нормально распределены.
подбираемые коэффициенты регрессии,
- компонента ошибки. Предполагается, что все ошибки независимы и нормально распределены.
Для построения регрессионных моделей необходимо иметь базу данных наблюдений примерно такого вида:
Таблица 1 Наблюдения для построения регрессионных моделей
| № | переменные | ||||
| независимые | зависимая | ||||
| X1 | X2 | ... | XN | Y | |
| 1 | x_11 | x_12 | ... | x_1N | Y_1 |
| 2 | x_21 | x_22 | ... | x_2N | Y_2 |
| ... | ... | ... | ... | ... | ... |
| M | x_M1 | x_M2 | ... | x_MN | Y_M |
С помощью таблицы значений прошлых наблюдений можно подобрать (например, методом наименьших квадратов) коэффициенты регрессии, настроив тем самым модель
При работе с регрессией надо соблюдать определенную осторожность и обязательно проверить на адекватность найденные модели. Существуют разные способы такой проверки. Обязательным является статистический анализ остатков, тест Дарбина-Уотсона. Полезно, как и в случае с нейронными сетями, иметь независимый набор примеров, на которых можно проверить качество работы модели.
Эконометрические методы прогнозирования
А) Средние и скользящие средние
Самой простой моделью, основанной на простом усреднении является
Y(t+1)=(1/(t))*[Y(t)+Y(t-1)+...+Y(1)], (11)
и в отличии от самой простой "наивной" модели, которой соответствовал принцип "завтра будет как сегодня", этой модели соответствует принцип "завтра будет как было в среднем за последнее время". Такая модель, конечно более устойчива к флуктуациям, поскольку в ней сглаживаются случайные выбросы относительно среднего. Несмотря на это, этот метод идеологически настолько же примитивен как и "наивные" модели и ему свойственны почти те же самые недостатки.
В приведенной выше формуле предполагалось, что ряд усредняется по достаточно длительному интервалу времени. Однако как правило, значения временного ряда из недалекого прошлого лучше описывают прогноз, чем более старые значения этого же ряда. Тогда можно использовать для прогнозирования скользящее среднее
Y(t+1)=(1/(T+1))*[Y(t)+Y(t-1)+...+Y(t-T)], (12)
Смысл его заключается в том, что модель видит только ближайшее прошлое (на T отсчетов по времени в глубину) и основываясь только на этих данных строит прогноз. При прогнозировании довольно часто используется метод экспоненциальных средних, который постоянно адаптируется к данным за счет новых значений. Формула, описывающая эту модель записывается как:
Y(t+1)=a*Y(t)+(1-a)*^Y(t), (13)
где Y(t+1) – прогноз на следующий период времени Y(t) – реальное значение в момент времени t ^Y(t) – прошлый прогноз на момент времени t a – постоянная сглаживания (0<=a<=1))
В этом методе есть внутренний параметр a, который определяет зависимость прогноза от более старых данных, причем влияние данных на прогноз экспоненциально убывает с "возрастом" данных. Зависимость влияния данных на прогноз при разных коэффициентах a приведена на графике.
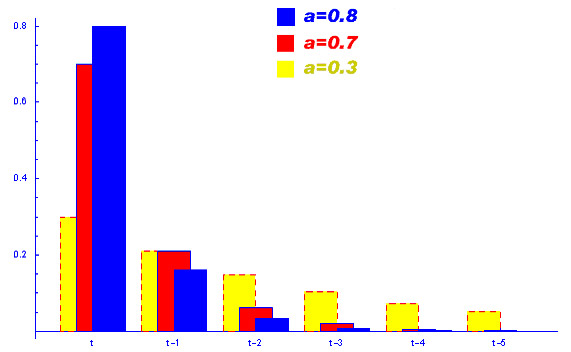
Рисунок 3 График зависимости данных на прогноз
Видно, что при a->1, экспоненциальная модель стремится к самой простой "наивной" модели. При a->0, прогнозируемая величина становится равной предыдущему прогнозу.
Б) Методы Хольта и Брауна
В середине прошлого века Хольт предложил усовершенствованный метод экспоненциального сглаживания, впоследствии названный его именем. В предложенном алгоритме значения уровня и тренда сглаживаются с помощью экспоненциального сглаживания. Причем параметры сглаживания у них различны.
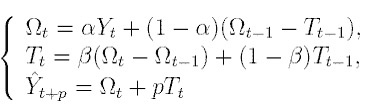 (14)
(14)
Здесь первое уравнение описывает сглаженный ряд общего уровня. Второе уравнение служит для оценки тренда. Третье уравнение определяет прогноз на p отсчетов по времени вперед.
Постоянные сглаживания в методе Хольта идеологически играют ту же роль, что и постоянная в простом экспоненциальном сглаживании. Подбираются они, например, путем перебора по этим параметрам с каким-то шагом. Можно использовать и менее сложные в смысле количества вычислений алгоритмы. Главное, что всегда можно подобрать такую пару параметров, которая дает большую точность модели на тестовом наборе и затем использовать эту пару параметров при реальном прогнозировании.
Частным случаем метода Хольта является метод Брауна, когда a=ß.
В) Метод Винтерса
Хотя описанный выше метод Хольта (метод двухпараметрического экспоненциального сглаживания) и не является совсем простым (относительно "наивных" моделей и моделей, основанных на усреднении), он не позволяет учитывать сезонные колебания при прогнозировании. Говоря более аккуратно, этот метод не может их "видеть" в предыстории. Существует расширение метода Хольта до трехпараметрического экспоненциального сглаживания. Этот алгоритм называется методом Винтерса. При этом делается попытка учесть сезонные составляющие в данных. Система уравнений, описывающих метод Винтерса выглядит следующим образом:
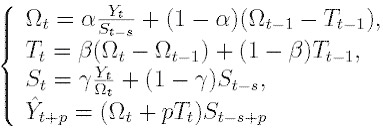 (15)
(15)
Дробь в первом уравнении служит для исключения сезонности из Y(t). После исключения сезонности алгоритм работает с "чистыми" данными, в которых нет сезонных колебаний. Появляются они уже в самом финальном прогнозе, когда "чистый" прогноз, посчитанный по методу Хольта умножается на сезонный коэффициент.
Работа современной и качественной системы невозможна без привлечения опыта специалиста в данной сфере. Также особое внимание следует обратить на полноту входной информации, на степень влияния различных факторов на задачу, в том числе и случайных. Достаточно сложно определить какие из факторов будут решающими при построении достоверного прогноза.
Оптимизация материальных затрат на ремонты – первоочередная цель многих предприятий Энергетического комплекса Украины. Как правило, все из них могут позволить себе купить дорогостоящие системы управления предприятием, но делают это единицы по той простой причине, что зарубежные системы данного класса не адаптированы для стран СНГ и время внедрения очень велико и проблематично. Но самым существенным недостатком таких систем является то, что они не занимаются непосредственной оптимизацией затрат и ни в одной из них не применяются математические методы анализа. Исследования, показали, что более эффективным будет внедрение системы оптимизации материальных и человеческих ресурсов, основанной на принципе нейронных сетей. В настоящее время можно с уверенностью сказать, что использование нейронных сетей при прогнозировании дает ощутимое преимущество по сравнению с более простыми статистическими методами.
Данная магистерская работа должна быть окончательна готова и защищена в декабре 2006 г.
1. B. Tinham, Power to the People. // Control and Instrumentation. №2. 1999. p.p.33-47
7. Стариков Алексей, Нейронные сети - математический аппарат, http://www.basegroup.ru/neural/