Донецкий Национальный Технический Университет


|
|
||||||||||||||||||||||||||
|
Автореферат к магистерской работе |
|
Актуальность Изучение основных морфо-функциональных принципов организации артериального русла большого круга кровообращения, является актуальной научной задачей, поскольку сосудистые заболевания в значительной степени обуславливают смертность и инвалидизацию населения. Высокая частота встречаемости и особая тяжесть этих заболевания требуют усовершенствования знаний в этой области и разработки новых, эффективных способов их диагностики и лечения, а также прогнозирования результатов хирургической коррекции гемодинамических расстройств. Цель и задачи Цель и задачей магистерской работы является создание программно-апаратного комплекса для расчёта оптимальных параметров морфо-функциональных принципов организации артериального русла большого круга кровообращения , на основе генетического алгоритма. Для достижения поставленной цели определены следующие задачи: 1 Изучить морфометрические закономерности артериальных русел функционально-различных органов большого круга кровообращения (скелетной мышцы, сердца, почек, головного мозга), влияющие на гемодинамическое сопротивление. 2 Создать математические модели, описывающие закономерности строения артериальных русел вышеперечисленных органов адаптированных для использования генетического алгоритма. 
Практическая значимость Сформулированные общие и индивидуальные морфо-функциональные принципы организации артериальных русел функционально-различных органов большого круга кровообращения будут способствовать лучшему пониманию законов, лежащих в основе их строения и функционирования. Смоделированные геометрические параметры модели кровеносных русел могут использоваться в качестве формализованного оценочного эталона нормального строения русел вышеперечисленных органов. Количественные данные об УКБС артерии могут служить отправной точкой для дальнейших исследований ее механических свойств и поведения при дилатации и разрушении. Использование созданной математической модели строения артериального русла в условиях эксперимента на компьютере даст возможность получения новых сведений о различных аспектах гемоциркуляции. Использование в будущем в клинических условиях: математических моделей строения артериальных русел функционально-различных органов большого круга кровообращения позволит в автоматическом режиме диагностировать их патологию, прогнозировать объем и площадь кровоснабжаемого участка, судить об адекватности кровоснабжения, в частности, использование математической модели артериального русла скелетной мышцы позволит рационально планировать объем трансплантируемого кожно-мышечного лоскута. Практическое применение математической модели гемодинамики в условиях эксперимента на компьютере даст возможность объективного планирования мероприятий по реконструкции патологически измененного артериального русла. Обзор существующих средств показывает, что сегодняшний день отсутствуют программные средства, которые позволяли бы на основе данных о входном диаметре сосуда восстанавливать всё сосудистое дерево данного органа, поэтому решаемая задача является исключительно важной для современной медицины. Теоретические сведения Впервые проблема функциональной анатомии сосудистых разветвлений была сформулирована в 1878 году в докторской диссертации немецкого анатома и эмбриолога Вильгельма Ру. На основании своих наблюдений он пришел к выводу, что форма сосудистого разветвления похожа на форму струи жидкости, вытекающей из отверстия трубки. Им впервые была установлена связь между величиной угла разветвления артериальной дихотомии и диаметрами просветов материнского ствола и его дочерних ветвей. Обнаруженные закономерности строения артериальных дихотомий он сформулировал в виде правил, получивших в специальной литературе название "правила Ру" : 1. Если некоторая артерия разветвляется на две одинаковые ветви, то они отходят под одинаковыми углами к основному стволу. 2. Если одна из двух ветвей тоньше другой, то более толстая ветвь, или продолжение основной артерии, образует с основным стволом меньший угол, чем тонкая ветвь. 3. Все ответвления, которые столь малы, что они практически не уменьшают основной ствол, отходят от него под большим углом. Для объяснения этих правил В. Ру предложил гипотезу о том, что конструкция и функционирование кровеносной системы отвечает принципу минимальных затрат биологического материала, израсходованного на ее построение, и принципу минимальной работы, необходимой для продвижения по ней крови. При этом артериальные дихотомии под влиянием гемодинамического фактора принимают конфигурации, которые для данных условий являются наилучшими из всех возможных, т. е. оптимальными. Английский физиолог Murray C. D. в 1926 году использовал изящный математический прием для анализа сосудистой дихотомии. Это позволило ему, избегая сложных вычислений, решить вопрос о соотношении диаметров и углов в сосудистой дихотомии при котором достигается минимум потерь энергии. Murray C. D. вывел формулу, позволяющую рассчитать оптимальную величину угла разветвления в сосудистой дихотомии. Модель Murray C. D. дает возможность количественно объяснить эмпирические правила Ру. |
 Рис. 1.1. Схема ветвления проводящего элемента. |
|
В новой редакции они были сформулированы в виде набора уравнений ветвления произвольной
артерии с диаметром d0 (рис. 1.1) на две
дочерние артерии с диаметрами d1 и d2
и углами ветвления α1 и α2 соответственно:
1. если d1≈d2, то α1≈α2; 2. если d1<d2, то α1>α2; 3. если d1<<d2 и d0≈d2, то α1≈90° , α2≈0. Если рассчитать параметры ветвления OABC, обеспечивающего доставку жидкости из точки O в точки B и C (рис. 1.1) с минимальными затратами энергии, то для углов оптимального ветвления можно получить:  (1.1). (1.1). Для формализации описания артериального русла его представляли в виде связанного графа, вершины которого соответствовали точкам разветвлений артерий, а ребра - артериальным сегментам. |
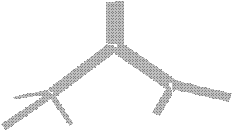 Рис. 1.2. Схема измерения участка артериального русла: Di - диаметр материнской артерии; dmin - минимальный диаметр ветви; dmax - максимальный диаметр ветви; L - длина артериального сегмента; CM - отношение числа артерий, выходящих из точки разветвления, к числу артерий, входящих в нее. |
|
На начальном этапе статистического исследования экстраорганную часть
артериального русла представляли как конструкцию, состоящую из взаимосвязанных
артериальных сегментов. Файл данных содержал следующую информацию: 1) Gr - номер генерации - порядковый номер вновь образовавшейся группы артерий, к которой относится данный сегмент ; при этом под "артерией" подразумевали линейную конструкцию, состоящую из дочерних сегментов с большим внутренним диаметром (если не выполняется одно из условий: D/dmax<3, dmax<>dmin или dmax>0,1, то артерия заканчивается); 2) i - уровень деления: вновь образовавшийся ряд артериальных сегментов (рис. 1.3); 3) внутренний диаметр (D) артериального сегмента (мм), 3) длина (L) артериального сегмента (мм) (расстояние между двумя ветвлениями); 4) фактор формы FF (отн.ед.) - отношение величины длины артериального сегмента к величине его радиуса (отн.ед.); 5) площадь поперечного сечения артериального сегмента (H= π*D2/4) (мм2); 6) площадь внутренней поверхности артериального сегмента (S=π*D*L) (мм2); 7) объем внутренней полости (V=H*L) артериального сегмента (мм3), 9) R0=128*L/π*D4 - морфологическая составляющая гемодинамического сопротивления (МСГС) (мм3) из уравнения Пуазейля (1.1); 10) CM - коэффициент 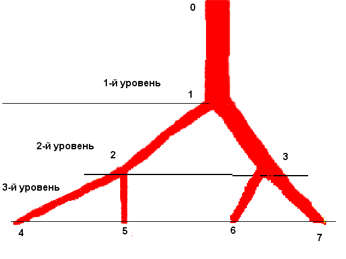 Рис. 1.3. Схематическое представление участка артериального русла. Примечание: сегменты 1-го уровня деления: 0-1; сегменты 2-го уровня деления: 1-2 и 1-3; сегменты 3-го уровня деления: 2-4, 2-5, 3-6, 3-7; сегменты 1-й генерации: 0-1, 1-3, 3-7; сегменты 2-ой генерации: 1-2, 2-4, 3-6; сегменты 3-й генерации: 2-5. увеличения количества артерий, равен - числу дочерних ветвей, образовавшихся в результате деления материнского артериального сегмента (отн.ед.). В последующем экстраорганную часть артериального русла большого круга кровообращения рассматривали как конструкцию, состоящую из взаимосвязанных артериальных разветвлений (рис. 1.4). Каждое разветвление образуют: артериальный сегмент, входящий в точку ветвления (материнский), артериальные сегменты, выходящие из нее (дочерние), и собственно точка разветвления. В качестве характеристики степени ветвления использовали показатель СМ - коэффициент увеличения количества артерий. Он мог быть равен 2 - дихотомия, 3 - трихотомия и 4 - квадритомия. 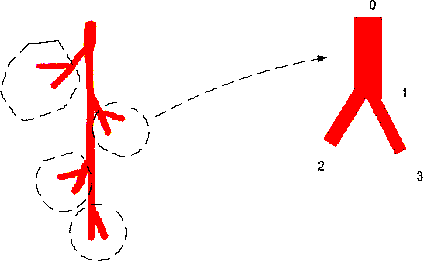 Рис. 1.4. Схема представления артериального русла как системы, состоящей из артериальных дихотомических разветвлений . Примечания: 0-1 - материнский артериальный сегмент, 1-2 - дочерний артериальный сегмент с большим диаметром, 1-3 - дочерний артериальный сегмент с меньшим диаметром, 1 - точка разветвления (собственно дихотомия). В основу теоретических построений идеального артериального дерева положен принцип минимальных затрат биологического материала и энергии. Предполагалось, что функцией сосудистого разветвления является проведение крови с минимальными затратами энергии. Реализация этого принципа осуществляется и проявляется, по мнению многих авторов путем согласования величин внутренних диаметров артерий, составляющих сосудистое разветвление. На базе описанной выше теории построена программа Vasculograph, которая моделирует структуру кровеносного русла используя некоторые средние значения показателей модели для определенных органов однако оптимум модели не всегда соответствует средним показателям поэтому необходимо использовать такой вид поиска оптимального решения при котором можно было без полного перебора всех возможных значений подобрать оптимальное решение. Методом который обеспечивает такой поиск является генетический алгоритм работающий на множестве вещественных чисел. В качестве фитнесс-функций, оценивающих параметры модели можно взять такие показатели как сопротивление и минимум расхода материала. Чтобы оценить расход материала достаточно оценить отношение объёма сосудистого русла к покрываемой им площади, чем это отношение меньше, тем расход материала меньше. Однако необходимо также учитывать также такие параметры как гемодинамическое сопротивление русла, объёмную скорость и давление крови, которые также стремится к минимуму для эффективного проведения крови по сосудам. Для того, что бы оценить параметры гемодинамики построенного русла нужно использовать следующую методику. Для расчета объемной скорости тока и давления необходимо учитывать характер соединения сосудов (последовательный или параллельный). При последовательном соединении сосудов, сопротивления их складываются: а при параллельном соединении складываются обратные величины сопротивлений: Сопротивление внутриорганных сосудов вплоть до уровня капилляров находилось с использованием данных модели деления сосудов, описанной выше. При этом сопротивление уровня вычислялось из условия параллельного соединения сосудов находящихся на данном уровне, а сопротивление всех уровней из условиях их последовательного соединения. Сопротивление капиллярного русла органов находилось из известного эмпирического соотношения , определяющего сопротивление капилляров как 1/3 от общего сопротивления внутриорганных сосудов данного органа. Используя эти уравнения можно найти регионарное сопротивление артериальной системы в любом заданном участке. Расчет объемной скорости тока в артериальной системе производился по формуле: где Qi - расход крови в ветви, отходящей непосредственно от основного ствола, Qo - расход крови в основном стволе, Ro -суммарное сопротивление всех артерий из системы основного ствола, Ri - суммарное сопротивление всех артерий из системы данной ветви. Поскольку расход крови в начальной части аорты считался заданным, то можно найти искомые величины для всех ветвей аорты, а затем рекуррентно по этой же формуле для ветвей этих ветвей и т.д. Среднее за цикл падение артериального давления на заданном сосуде находилось из соотношения:где dP0-общее падение давления в системе, Ri- сопротивление данного сосуда, Ro - общее сопротивление сосудов, включенных с данным последовательно. Рассмотрим кратко принцип работы генетического алгоритма (ГА). Генетический алгоритм Генетические Алгоритмы - адаптивные методы поиска, которые в последнее время часто используются для решения задач функциональной оптимизации. Они основаны на генетических процессах биологических организмов: биологические популяции развиваются в течении нескольких поколений, подчиняясь законам естественного отбора и по принципу "выживает наиболее приспособленный" (survival of the fittest), открытому Чарльзом Дарвином. Подражая этому процессу генетические алгоритмы способны "развивать" решения реальных задач, если те соответствующим образом закодированы. Например, ГА могут использоваться, чтобы проектировать структуры моста, для поиска максимального отношения прочности/веса, или определять наименее расточительное размещение для нарезки форм из ткани. Они могут также использоваться для интерактивного управления процессом, например на химическом заводе, или балансировании загрузки на многопроцессорном компьютере. Вполне реальный пример: израильская компания Schema разработала программный продукт Channeling для оптимизации работы сотовой связи путем выбора оптимальной частоты, на которой будет вестись разговор. В основе этого программного продукта и используются генетические алгоритмы. Основные принципы ГА были сформулированы Голландом (Holland, 1975), и хорошо описаны во многих работах. В отличии от эволюции, происходящей в природе, ГА только моделируют те процессы в популяциях, которые являются существенными для развития. Точный ответ на вопрос: какие биологические процессы существенны для развития, и какие нет? - все еще открыт для исследователей. В природе особи в популяции конкурируют друг с другом за различные ресурсы, такие, например, как пища или вода. Кроме того, члены популяции одного вида часто конкурируют за привлечение брачного партнера. Те особи, которые наиболее приспособлены к окружающим условиям, будут иметь относительно больше шансов воспроизвести потомков. Слабо приспособленные особи либо совсем не произведут потомства, либо их потомство будет очень немногочисленным. Это означает, что гены от высоко адаптированных или приспособленных особей будут распространятся в увеличивающемся количестве потомков на каждом последующем поколении. Комбинация хороших характеристик от различных родителей иногда может приводить к появлению "суперприспособленного" потомка, чья приспособленность больше, чем приспособленность любого из его родителя. Таким образом, вид развивается, лучше и лучше приспосабливаясь к среде обитания. ГА используют прямую аналогию с таким механизмом. Они работают с совокупностью "особей" - популяцией, каждая из которых представляет возможное решение данной проблемы. Каждая особь оценивается мерой ее "приспособленности" согласно тому, насколько "хорошо" соответствующее ей решение задачи. Например, мерой приспособленности могло бы быть отношение силы/веса для данного проекта моста. (В природе это эквивалентно оценке того, насколько эффективен организм при конкуренции за ресурсы.) Наиболее приспособленные особи получают возможность "воспроизводит" потомство с помощью "перекрестного скрещивания" с другими особями популяции. Это приводит к появлению новых особей, которые сочетают в себе некоторые характеристики, наследуемые ими от родителей. Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести потомков, так что те свойства, которыми они обладали, будут постепенно исчезать из популяции в процессе эволюции. Так и воспроизводится вся новая популяция допустимых решений, выбирая лучших представителей предыдущего поколения, скрещивая их и получая множество новых особей. Это новое поколение содержит более высокое соотношение характеристик, которыми обладают хорошие члены предыдущего поколения. Таким образом, из поколения в поколение, хорошие характеристики распространяются по всей популяции. Скрещивание наиболее приспособленных особей приводит к тому, что исследуются наиболее перспективные участки пространства поиска. В конечном итоге, популяция будет сходиться к оптимальному решению задачи. Имеются много способов реализации идеи биологической эволюции в рамках ГА. Традиционным считается ГА, представленный на схеме. НАЧАЛО /* генетический алгоритм */ Создать начальную популяцию Оценить приспособленность каждой особи останов := FALSE ПОКА НЕ останов ВЫПОЛНЯТЬ НАЧАЛО /* создать популяцию нового поколения */ ПОВТОРИТЬ (размер_популяции/2) РАЗ НАЧАЛО /* цикл воспроизводства */ Выбрать две особи с высокой приспособленностью из предыдущего поколения для скрещивания Скрестить выбранные особи и получить двух потомков Оценить приспособленности потомков Поместить потомков в новое поколение КОНЕЦ ЕСЛИ популяция сошлась ТО останов := TRUE КОНЕЦ КОНЕЦ В последние годы, реализовано много генетических алгоритмов и в большинстве случаев они мало похожи на этот ГА. По этой причине в настоящее время под термином "генетические алгоритмы" скрывается не одна модель, а достаточно широкий класс алгоритмов, подчас мало похожих друг от друга. Исследователи экспериментировали с различными типами представлений, операторов кроссовера и мутации, специальных операторов, и различных подходов к воспроизводству и отбору. Хотя модель эволюционного развития, применяемая в ГА, сильно упрощена по
сравнению со своим природным аналогом, тем не менее ГА является достаточно
мощным средством и может с успехом применяться для широкого класса прикладных
задач, включая те, которые трудно, а иногда и вовсе невозможно, решить другими
методам. Однако, ГА, как и другие методы эволюционных вычислений, не гарантирует
обнаружения глобального решения за полиномиальное время. ГА-мы не гарантируют и
того, что глобальное решение будет найдено, но они хороши для поиска "достаточно
хорошего" решения задачи "достаточно быстро". Там, где задача может быть решена
специальными методам, почти всегда такие методы будут эффективнее ГА и в
быстродействии и в точность найденных решений. Главным же преимуществом ГА-мов
является то, что они могут применяться даже на сложных задачах, там, где не
существует никаких специальных методов. Даже там, где хорошо работаю
существующие методики, можно достигнуть улучшения сочетанием их с ГА.
|