|
При решении дифференциальных уравнений и систем (например, системы линейных дифференциальных
уравнений [2]) часто используются матрично–векторные арифметические операции: умножение, сложение
и другие. Наиболее подходящими в плане коммуникационных затрат для таких операций являются
топологии [1, c.32–36]: кольцо, решётка (решётка-тор и её модификации) и гиперкуб. Далее будут рассматриваться
только для топологии типа кольцо и решётка. Структура топологии решётки–тора представлена на
рисунке 1.1, структура топологии кольца – на рисунке 1.2.
Рисунок 1.1 – Структура топологии решётки–тора
Рисунок 1.2 – Структура топологии кольца
Для топологии типа решётка вычисление матрично–векторных арифметических операций
можно свести к выполнению операций аналогичного типа над прямоугольными блоками матриц (далее
будут рассматриваться только квадратные матрицы и их блоки – непрерывные квадратные подматрицы).
Исходной матрице может быть поставлена в соответствие матрица, элементами которой служат блоки исходной.
Блоки матрицы могут различным образом отображаться на узлы вычислительной решётки. Для
математического описания отображения блоков вводится одномерная функция отображения. По исходному
номеру блока матрицы функция вычисляет номер узла вычислительной решётки, на который блок будет
отображён. Вид функции отображения задаётся формулой (1.1), где:
- i задаёт индекс строки/столбца матрицы,
- p представляет размерность вычислительной решётки по любому из измерений,
- pi задаёт индекс узла вычислительной решётки в строке/столбце, на котором находится
блок матрицы с индексом i.
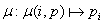 (1.1) (1.1)
Пусть рассматривается матрица, элементы которой являются блоками исходной матрицы. Если ввести
несвязанные функции отображения блоков строк матрицы и столбцов, становится возможным описать
отображение блоков матрицы на узлы вычислительной решётки. Существуют ограничения для отображений
строк и столбцов матриц, участвующих в параллельном алгоритме вычисления произведения, –
алгоритмическая совместимость матриц. Соблюдение свойства обеспечивает корректность получаемого
результата при правильной реализации параллельного алгоритма.
Сложение матриц сводится к однократному матричному сложению соответствующих блоков матриц–операндов.
Умножение матриц является более сложным и может быть эффективно выполнено с помощью ряда алгоритмов
семейств Кэннона и Фокса [3, c. 6-7]. Алгоритмы семейства Кэннона по коммуникационным затратам являются
более предпочтительными по отношению к алгоритмам семейства Фокса.
Алгоритмы семейства Фокса не меняют отображения блоков матриц–операндов и матрицы–результата на узлы
вычислительной решётки. Особенностью алгоритмов Кэннона является смена отображения блоков одной из
матриц–операндов или матрицы–результата на узлы вычислительной решётки. Существуют модификации
алгоритма Кэннона, которые сохраняют отображение блоков одной из матриц на узлы вычислительной
решётки [4, c. 26-55].
Вычислительная сложность обоих алгоритмов без учета затрат на коммуникацию определяется формулой
(1.2), где:
- p – число процессоров в измерении решётки–тора;
- k – размерность блока матриц;
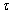 – модельный такт времени (время выполнения операции над числами с плавающей точкой).
– модельный такт времени (время выполнения операции над числами с плавающей точкой).
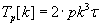 (1.2) (1.2)
Пример выполнения параллельного алгоритма Фокса для матрицы размерности 3 представлен на рисунке
1.3. Пример выполнения параллельного алгоритма Кэннона (систолического алгоритма) для матрицы
размерности 3 представлен на рисунке 1.4.
Рисунок 1.3 – Пример выполнения алгоритма Фокса для матриц 3*3
Рисунок 1.4 – Пример выполнения алгоритма Кэннона для матриц 3*3
Умножение матрицы на вектор может быть сведено к умножению матрицы на матрицу. Пусть блок вектора
– набор исходной непрерывной последовательности элементов вектора. Тогда из блоков вектора можно
построить псевдо матрицу, обладающую следующими особенностями [2, c.2]:
- блок псевдо матрицы будет представлять собой блок вектора;
- блоки каждого столбца псевдо матрицы будет в совокупности представлять исходный вектор.
При выполнении этих условий можно осуществить умножение матрицы на вектор по модифицированному
алгоритму вычисления произведения матриц. Модификация исходного алгоритма будет проявляться при
умножении блоков матрицы и вектора.
Вычислительная сложность параллельных алгоритмов Фокса и Кэннона вычисления результата матрично–
векторного произведения без учёта затрат на коммуникацию определяется формулой (1.3).
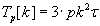 (1.3) (1.3)
|