|
Matrix–vector operations are widely used in solving of differential equations and its systems (for example, systems of
linear ordinary differential equations [2]). These operations are multiplication, addition etc. The most suitable topologies
[1, c.32–36] for performing matrix–vector operations are ring, grid (torus–grid and its modifications) and hypercube. Only
ring and grid will be discussed below. Structures of torus–grid and ring topologies are shown on figures 1.1 and 1.2
respectively.
Figure 1.1 – Structure of torus–grid topology
Figure 1.2 – Structure of ring topology
On the grid topology matrix–vector computational operations can be reduced to computations over rectangular matrix
(vector) blocks (in the text below only square matrixes and their square sub matrixes will be covered).
Original matrix could be associated with a modified matrix. Elements of such modified matrix are blocks of the original
matrix. There are various ways of original matrix blocks distribution among the processor units of the grid. Such
distributions are described mathematically by the formal one–dimensional distribution function. Original index of the
matrix block is the argument of this function. Return value is interpreted as an index of the processor unit of the grid in
fixed dimension. Distribution function is defined by the formula (1.1), where:
- i – index of the processor unit of the grid in fixed dimension,
- p – size of fixed dimension of the grid,
- pi index of the processor unit in the row/column of the grid, where the block described by the i index
is distributed
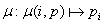 (1.1) (1.1)
Let the modified matrix have elements that are the blocks of the original matrix. And there are two independent distribution
functions for the rows and columns of the modified matrix. In this case elements of the modified matrix can be unambiguously
distributed on the processor units of two–dimensional grid. Row and column distribution functions can’t be mentioned as
arbitrary in the parallel matrix multiplication algorithm. This algorithm imposes constraints on these functions. These
constraints are known as an algorithmic compatibility of matrixes in parallel matrix multiplication algorithms.
Such characteristics compliance ensures correctness of the algorithm’s result in case of its correct implementation.
Matrix summation is reduced to the single–stage addition of the appropriate blocks of the matrixes.
Matrix multiplication is more complex then the addition and could be performed efficiently by the Cannon’s and Fox’s
algorithms [3, c. 6-7]. Cannon’s algorithms are more efficient then Fox’s algorithms.
Fox’s algorithms don’t change block distribution on the processor units of the matrixes being multiplied. Cannon’s algorithms
don’t behave in such manner. There are modifications of the Cannon’s systolic algorithm that don’t change block distribution
of the concrete matrix (result matrix or one of the operand matrixes) [4, c. 26-55].
Computational complexity of each of the algorithms (without communicational overhead) is described by formula (1.2), where:
- p – number of processor units in the dimension of the grid,
- k – matrix block dimension,
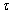 – clock tick (time of one floating point operation).
– clock tick (time of one floating point operation).
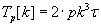 (1.2) (1.2)
The example of Fox algorithm for the 3*3 matrix is shown on figure 1.3. The example of
Cannon (systolic) algorithm for the 3*3 matrix is shown on figure 1.4.
Figure 1.3 – The example of Fox algorithm for the 3*3 matrix
Figure 1.4 – The example of Cannon (systolic) algorithm for the 3*3 matrix
Matrix–vector multiplication can be reduced to the matrix multiplication. Let the operand vector be sliced on the blocks of
the same size. In this case pseudo matrix of the special structure can be mentioned. Such pseudo matrix consists of blocks of
the original vector and can be characterized as followed [2, c.2]:
- pseudo matrix blocks are equivalent to the original vector blocks;
- blocks of each column of pseudo matrix in the aggregate are equivalent to the original vector.
In case of fulfillment of conditions mentioned above matrix–vector multiplication operation could be performed as
modified matrix multiplication algorithm. Modification of the algorithm takes place in the matrix–vector blocks multiplication.
Computational complexity of the parallel Fox and Cannon algorithms (without communicational overhead) is described by
formula (1.3).
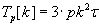 (1.3) (1.3)
|