|
Communicational overhead of matrix–vector multiplication operations might be effectively used for the Cauchy
problem (3.1) solving for the systems of linear ODE.
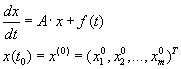 (3.1) (3.1)
This problem might be solved according to the Runge–Kutta method (3.2). Appropriate formula defines iteration process
that can be reduced to the arithmetical matrix–vector operations [2, c.1].
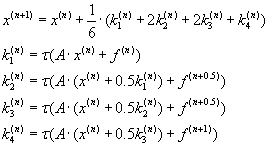 (3.2) (3.2)
All intermediate factors ki can be calculated in the consistently way only. Parallelism can be realized
during the calculation of each of factor. It can be reached via using parallel matrix–vector arithmetic operations
described above.
Alternative method of the Cauchy problem solving according to the Runge–Kutta rule is calculation of the full transitional
operator (matrix). This operation is performed preliminary and once (before performing of iterations of a method) according
to the formula (3.3). Thus, whole iterative process is reduced to a series of consecutive matrix–vector multiplication
operations [2, c.3-5].
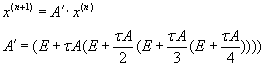 (3.3) (3.3)
Advantage of the approach with transitional matrix calculation is shown at a plenty of iterations of Runge–Kutta method.
Therefore, for the certain limited quantity of iterations the best characteristics will be shown by the approach with calculation
of intermediate factors.
Characteristic feature of algorithms of Runge–Kutta method is iterative process of Cauchy problem solving. Parallelism is
exposed during the calculation of intermediate factors on each step of method. Computational dependence of intermediate
factors generally does not allow to perform simultaneous calculations of approximated solutions on different steps of
Runge–Kutta method.
Parallelism of algorithm of Runge–Kutta method with calculation of intermediate factors on a step can be exposed at a stage
of performing of matrix–vector operations. So computation step overhead of the parallel algorithm is defined by the formula
(3.4). Parallel algorithm version of N-step-by-step Runge–Kutta method can be accomplished by the time defined by formula
(3.5). Cannon algorithm with unchanged block distribution of operand–matrix is the most suitable for performing matrix–vector
multiplication.
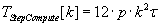 (3.4) (3.4)
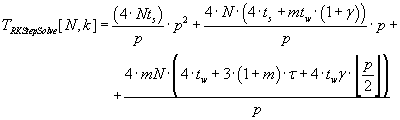 (3.5) (3.5)
Acceleration and efficiency of processor units using of parallel algorithm are defined by formulas (3.6) and (3.7)
correspondingly.
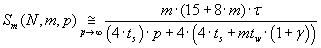 (3.6) (3.6)
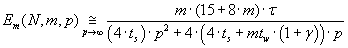 (3.7) (3.7)
In order to avoid of intermediate factors calculation on each step of Runge–Kutta method transposition operator (matrix)
should be used. Thus vector of the variables calculation is only performed on current iteration. Parallelization of
transposition matrix calculation should be performed via using Cannon’s algorithm with unchanged result–matrix
block distribution. Calculation of the approximate solution on the next iteration can be performed via calculation of
matrix–vector product by the Cannon algorithm mentioned above.
Computational overhead of parallel algorithm of transition matrix calculation (3.3) is defined by formula (3.8).
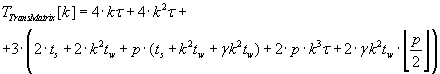 (3.8) (3.8)
Formula (3.9) reflects an equivalent of parallel algorithm acceleration function for large values of p. Efficiency of
processor units using of parallel algorithm is defined by the formula (3.10).
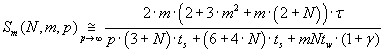 (3.9) (3.9)
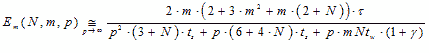 (3.10) (3.10)
Let the algorithm of the Cauchy problem solving for linear ODE system with calculation of intermediate factors via
Runge–Kutta method is designated through RKStepSolve. Therefore the alternative algorithm with preliminary
calculation of a transition matrix is designated through RKTransMatrix.
Execution time functions of parallel algorithms RKStepSolve and RKTransMatrix are shown on figures 3.1 and 3.2.
Figure 3.1 – Dependence of parallel algorithms execution time on the dimension of a computational grid for the fixed
problem dimension
Figure 3.2 – Dependence of parallel algorithms execution time on the dimension of matrixes and vectors for the fixed
dimension of a computational grid
Figure 3.3 reflects dependence of execution time of parallel algorithms RKStepSolve and RKTransMatrix on steps count for
the fixed dimensions of a computational grid and dimension of the initial problem.
Figure 3.3 – Dependence of execution time of parallel algorithms on steps count for the fixed dimensions of a computational
grid and dimension of the initial problem
|