|
Data time transfer of the distributed–memory computer systems depends on [1, p.50–51]:
- latency (ts) – time for preparing to the communication (is measured from the initiation moment of the
operation);
- machine word transfer time (tw) from one processor unit to another.
Evidently, data transfer time is proportional to the amount of transferred data (for the large amount of transferred data)
[1, p.48-69]. Therefore, reducing the size of transferred data causes decreasing of parallel algorithm total time execution.
Thus, parallel matrix–vector multiplication algorithm in general is more efficient then appropriate parallel matrix multiplication
algorithm. As the result several statements might be set:
- parallel matrix–vector multiplication algorithms are more efficient in general case than parallel matrix multiplication
algorithms;
- previous characteristic might be violated in case of transferring of matrix blocks in parallel matrix–vector multiplication
algorithm;
- the most efficient parallel matrix–vector multiplication algorithm has the lowest count of communication operations /
(transferred amount of data).
One of features of Cannon’s algorithms is changing the original distribution of blocks of the operands (A, B) or result
(C) during algorithm execution. Only one of the objects (matrix or vector) will be left unchanged in terms of block distribution
[4, p. 26–55]. Let the matrix with unchanged distribution is mentioned in the algorithm’s signature.
The whole parallel algorithms execution times are characterized by formulas (2.1) – (2.3) respectively. These
algorithms leave the block distribution of matrixes A, B and C respectively unchanged.
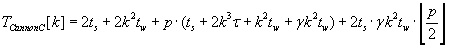 (2.1) (2.1)
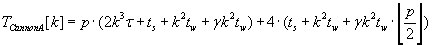 (2.2) (2.2)
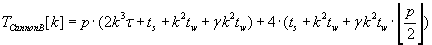 (2.3) (2.3)
As the result of analyzing of formulas (2.1), (2.2) è (2.3) the most efficient is algorithm with unchanged block distribution of
matrix C. Its advantage is caused by the lowest communication overhead against other two algorithms.
Fox’s algorithms leave the block distribution of matrixes unchanged. There are no primary and final alignings of matrix blocks
in these algorithms.
Disadvantage of Fox’s algorithms is necessity to use broadcast operation on each step of the algorithm. As the result such
behavior causes more communication overhead then Cannon’s algorithms show. The whole time of Fox’s algorithms
execution is described by formula (2.4).
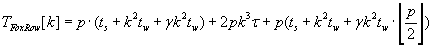 (2.4) (2.4)
Comparative diagram of algorithms execution times is shown on figure (2.1). Dimension of matrix blocks is constant,
count of the processor units is variable.
Figure 2.1 – Communication overhead of the algorithms (final aligning in the Cannon’s algorithms is taken in account)
As it was mentioned above, difference of the algorithms is caused by different communication overhead and by the final distribution
of matrix blocks. Fox’s algorithms show the worthless execution time in comparison with
Cannon’s algorithms. Such decision is proved by formulas (2.1)–(2.4).
Matrix multiplication is equivalent to the matrix–vector multiplication of the original matrix on the vector–columns of other operand
matrix. Columns elements calculations of result matrix can be performed simultaneously.
In the matrix–vector multiplication operand vector might be changed on the pseudo matrix with the same columns. In this case
result matrix can be calculated via multiplication of original operand matrix and pseudo matrix. Any of algorithms listed above can
be used.
The whole time of Cannon’s algorithms execution for matrix–vector multiplication is described by formulas (2.5) – (2.7). As the result
of these algorithms execution block distribution of objects C, A è B respectively is left unchanged.
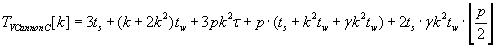 (2.5) (2.5)
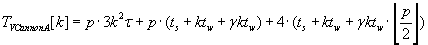 (2.6) (2.6)
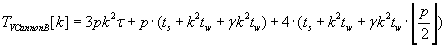 (2.7) (2.7)
According to the formulas (2.5), (2.6) and (2.7) Cannon’s algorithm with the unchanged operand matrix A has the lowest total
execution time. This result is gained by communicating by only vector blocks.
Formulas (2.5) and (2.7) prove that Cannon algorithm with unchanged matrix A is better then other two Cannon algorithms.
The whole time of execution of row and column Fox’s algorithms are mentioned by formulas (2.8) and (2.9). Comparison of
these formulas shows that column Fox algorithm is better then row Fox algorithm.
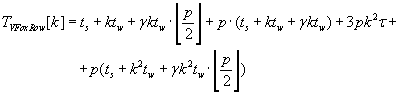 (2.8) (2.8)
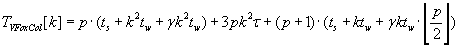 (2.9) (2.9)
Figure 2.2 shows graphical relations between total execution time of mentioned parallel matrix–vector multiplication algorithms
for fixed dimension of operand blocks and variable count of processor units.
Figure 2.2 – Parallel matrix–vector algorithms communication overhead
|