Автореферат выпускной работы магистра
на тему "Анализ и оценка эффективности параллельных разностных методов решения ОДУ на кластере"
Автор: Д.А. Завалкин, магистрант
Донецкий национальный технический университет
e-mail: dimzav@gmail.com [dimzav at gmail dot com]
Руководитель: Л.П. Фельдман, профессор, д.т.н
Донецкий национальный технический университет
Украина, 83001, Донецк, ул. Артема, 66.
тел. (062)3010856, e-mail: feldman@r5.dgtu.donetsk.ua
Анализ и оценка эффективности параллельных разностных методов решения ОДУ на кластере
Задачи, порождающие ОДУ, актуальность параллельных методов их решения
Моделирование реальных экономических, технических и других процессов, описываемых системами обыкновенных дифференциальных уравнений (СОДУ) большой размерности, представляет собой обширный класс задач, для решения которых применение высокопроизводительной вычислительной техники не только оправдано, но и необходимо. Об этом свидетельствует знаменитый список проблем "большой вызов", в котором такие задачи занимают одно из ведущих мест. Как результат, появилась проблема создания новых, высокоточных (10-15 – 10-20) методов численного интегрирования таких систем. Традиционный подход к решению этой проблемы, а именно применение явных методов Рунге-Кутты высоких порядков является неэффективным из-за многократного вычисления правых частей дифференциальных уравнений [1,2]. Методы численного интегрирования, использующие "старшие" производные, также вызывают трудности, поскольку в реальных задачах не всегда можно вычислить производные аналитически. Благодаря бурному развитию вычислительной техники в последние годы появилась возможность использовать несколько вычислительных машин для решения одной задачи, это породило проблему построения параллельных аналогов для известных последовательных алгоритмов. В частности, многие алгоритмы, успешно используемые в последовательных вычислениях, оказываются не применимыми при проведении параллельных вычислений. Отсюда вытекает необходимость построения специальных методов, адаптированных к вычислительным системам с параллельной архитектурой, распараллеливание вычислений в существующих последовательных методах не дает большого выигрыша от использования вместо одной вычислительной машины нескольких. При этом следует учитывать, что метод должен обладать численной устойчивостью и иметь оптимальную для сохранения эффективности структуру. Данным требованиям удовлетворяют блочные методы [3].
В блочных методах для блока из k точек новые k значений функции вычисляются одновременно, что вполне согласуется с архитектурой параллельных вычислительных систем. Такой принцип позволяет вычислять коэффициенты разностных формул не в процессе интегрирования, а на этапе разработки метода, что значительно увеличивает эффективность счета. В то же время для блочных методов отсутствуют оценки погрешностей и условия сходимости.
Последовательный метод
В общем случае методы Рунге-Кутта записывают в виде
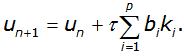
Здесь:
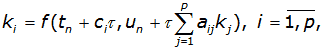
– константы
Число p, показывающее количество вспомогательных точек kj, используемых для вычисления основной точки ki, называется порядком метода.
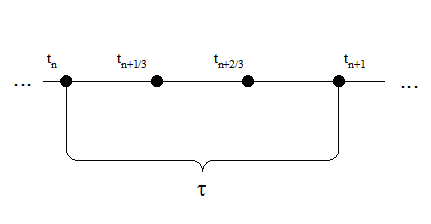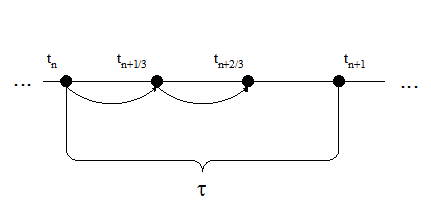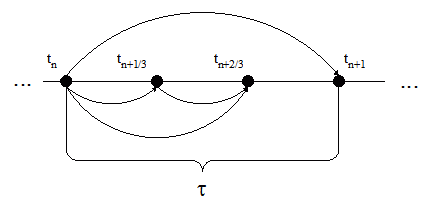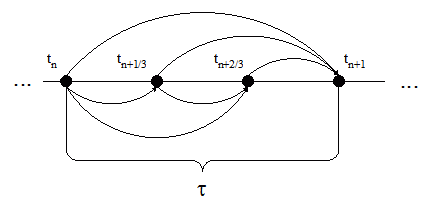
Рисунок 1 – Схема решения по классической формуле Рунге-Кутты 4-го порядка точности
(Анимация, 7 кадров, 10.7 Кб. Для повторения анимации обновите страницу)
Параллельные одношаговые методы
Рассмотрим решение задачи Коши
f(t,x), x(t0) = x0 (1)
k-точечным блочным разностным методом. Множество M точек равномерной сетки tm, m=1,2,…,M и tM=T с шагом
разобьем на N блоков, содержащих по k точек, при этом kN ≥ M. В каждом блоке введем номер точки i =0,1,…,k и обозначим через tn,i точку n –го блока с номером i. Точку tn,0 назовем началом блока n, а tn,k – концом блока. Очевидно, что имеет место tn,k = tn+1,0 . Условимся начальную точку в блок не включать [2].
Рисунок 2 – Схема разбиения на блоки множества M точек равномерной сетки tm
Если для расчета значений в новом блоке используется только последняя точка предшествующего – блочный метод считается одношаговым, а если все точки предшествующего блока – многошаговым.
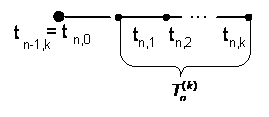
Рисунок 3 – Шаблон разностной схемы одношагового блочного метода
В общем случае уравнения одношаговых разностных методов для блока из k точек с учетом введенных обозначений можно записать в виде
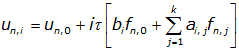(2)
– номер точки
– номер шага
Для решения полученной нелинейной системы уравнений можно использовать:
- итерационный метод;
- метод Ньютона.
Для того, чтобы сделать вывод о целесообразности реализации и выгоде, получаемой при применении параллельного метода необходимо знать его ускорение и коэффициент параллелизма.
Введем обозначения:
tf – время вычисления значения функции f(t,x);
tсл – время выполнения операции сложения;
tум – время выполнения операции умножения;
tоб – время передачи числа соседнему процессору.
Время вычисления на одном процессоре с точностью O(τk+1) во всех k узлах блока по формулам Рунге-Кутта k+1 порядка точности равно
(3)
Время параллельного вычисления на k процессорах приближенных значений решения во всех k узлах блока равно
(4)
Тогда ускорение параллельного одношагового k-точечного алгоритма равно
(5)
Коэффициент эффективности параллельного алгоритма вычисляется по формуле
(6)
Здесь Nпроц – количество используемых процессорных элементов. В нашем случае
(7)
Поэтому
(8)
Реализация параллельных методов в gridMathematica (Parallel Computing Toolkit)
Реализация параллельных алгоритмов на языке программирования – трудоемкая задача, и чем сложнее алгоритм, тем сложнее его реализовать оптимальным образом. Поэтому для упрощения реализации параллельных алгоритмов были разработаны специальные библиотеки, содержащие оптимальную реализацию многих рутинных операций, к примеру, параллельного сложения и вычитания набора чисел. Наиболее известная библиотека параллельного программирования – MPI, поддерживает много языков программирования, обеспечивает высокую скорость работы полученной в конце разработки программы, но время, затраченное на реализацию алгоритма с ее помощью довольно велико, порядка нескольких месяцев для достаточно сложных алгоритмов. Однако существует библиотека Parallel Computing Toolkit, разработанная компанией Wolfram Research, которая позволяет реализовывать параллельные алгоритмы на языке Mathematica, который ориентирован на символьные и численные вычисления и по этой причине является более привлекательным для реализации численных математических алгоритмов, чем языки C++ и Fortran, на которых чаще всего реализуют численные алгоритмов с использованием библиотеки MPI.
Приведем пример параллельного решения простой задачи на языке Mathematica с использованием библиотеки Parallel Computing Toolkit. Для этого возьмем одношаговый четырехточечный блочный метод и распараллелим вычисление правых частей ОДУ (см. рис. 4). Построим график зависимости времени выполнения алгоритма от количества используемых процессоров (см. рис. 5). В качестве тестовой задачи рассмотрим решение умеренно устойчивой задачи x' = - 10(t-1)x, x(0)=1.
Einschrit[k_,A_,B_,a_,b_]:=Block[{ai,v,q,V,Q,QI},
Array[b,k];
Array[v,k];
Array[q,{k,k}];
Array[a,{k,k}];
Do[Do[q[l-1,j]=j^(l-1),{j,1,k}],{l,2,k+1}];
Q=Array[q,{k,k}];
QI=Inverse[Q];
Do[Do[v[l-1]=i^(l-1)/l,{l,2,k+1}];
V=Array[v,k];
ai=QI.V;
Do[a[i,j]=ai[[j]],{j,1,k}],{i,1,k}];
Do[b[i]=1;Do[b[i]=b[i]-a[i,j],{j,1,k}],{i,1,k}];
B=Array[b,k];
A=Array[a,{k,k}]
];
f[t_,x_]:=-10*(t-1)*x;
Clear[a,b,A,B]
Einschrit[4,A,B,a,b];
Needs["Parallel`"];
maxSlaves=4;
timespent=Table[0,{maxSlaves}];
For[ii=1,ii≤maxSlaves,ii++,LaunchSlave["localhost",$mathkernel];
starttime=AbsoluteTime[];
k=4;q=30;n=(q+l)*k;t0=0;u0=1;tau=0.0174;l=6;
Array[w,{n,2},0];
fn=f[t0,u0];
un=u0;
tn=t0;
w[0,0]=t0;
w[0,1]=u0;
ie=ParallelTable[1,{i,k}];
Array[g, {k, k + 1}];
Do[Do[g[i, j +1] = i*a[i, j], {j, 1, k}], {i, k}];
Do[g[i, 1] =i*B[[i]], {i, k}];
G =Array[g, {k, k+ 1}];
Do[U = ParallelTable[un + i*tau*fn, {i, 0, k}];
Do[F = ParallelTable[f[tn + i*tau,un + i*tau*fn], {i, 0, k}];
V = un*ie + tau*G. F; U = Prepend [V, un], {j , l}];
r=s*k;
Do[w[r + i, 0] = tn + i*tau;w[r+i,1] =V[[i]], {i, k}];
un = V [[k]] ; tn = tn + k*tau; fn = f[tn, un] , {s , 0, q}] ;
timespent[[ii]]=AbsoluteTime[]-starttime;
];
CloseSlaves[];
Рисунок 4 – Пример параллельной реализации одношагового четырехточечного метода
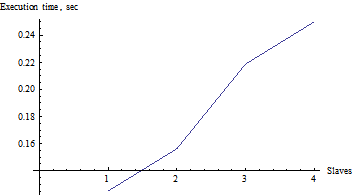
Рисунок 5 – График зависимости времени выполнения алгоритма от количества используемых процессоров
Для данной простой задачи и данного параллельного алгоритма мы видим, что использование нескольких процессоров не дает выигрыша во времени, время решения задачи только увеличивается за счет времени, затраченного на передачу данных между процессорами. Необходимо проводить дальнейшие исследования для других ОДУ и других параллельных одношаговых методов решения задачи Коши.
Литература
- Хайрер Э., Нёрсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи: Пер. с англ. – М.: Мир, 1990. – 512с.
- Арушанян О.Б., Залеткин С.Ф. Численное решение обыкновенных дифференциальных уравнений на Фортране.– М.: МГУ,1990.–336с.
- Системы параллельной обработки: Пер. с англ./ Под. ред. Ивенса Д.- М.: Мир,1985-416с.
- Фельдман Л.П. Сходимость и оценка погрешности параллельных одношаговых блочных методов моделирования динамических систем с сосредоточенными параметрами // Научные труды ДонНТУ. Серия: Информатика, моделирование и вычислительные методы, (ИКВТ-2000), выпуск 15: Донецк: ДонНТУ, 2000, с. 34-39.