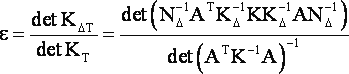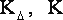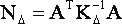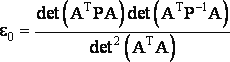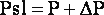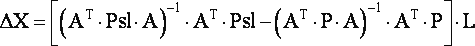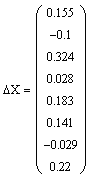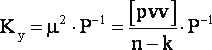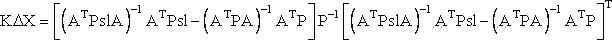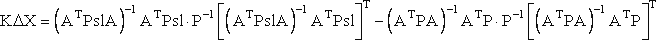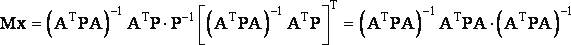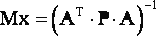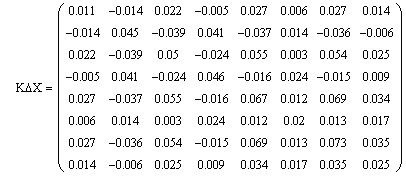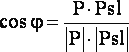Автореферат магистерской работы
Актуальность темы
На практике часто веса измерений известны с некоторыми погрешностями. Эти погрешности могут оказывать существенное влияние на результаты уравнивания и оценку точности сетей полигонометрии, а могут совсем не оказывать никакого влияния. Поэтому необходимо разработать некоторый критерий оценивания влияния ошибок весов.
Цель исследования и планируемый практический результат
Целью исследования является нахождение той минимальной величины ошибки веса, которая не оказывает влияния на точность уравнивания сетей полигонометрии, а также разработка некоторого универсального графика, который бы отражал влияние ошибок весов измерений с учётом формы и конфигурации конкретной сети.
Обзор состояний исследований и разработок по теме
Многие известные научные деятели занимались исследованием данной проблемы. Разработанные ими алгоритмы опираются на следующие обобщённые критерии точности, которые являются идентичными по выдаваемым результатам и показывают некоторую обобщённую точность всей геодезической сети в целом:
- обобщённая дисперсия, т.е. det K (здесь К - корреляционная матрица уравненных результатов измерений или параметров);
- среднее весовое от элементов корреляционной матрицы К, например Sp(FK) (здесь Sp - символ следа матрицы, F - произвольно определённая матрица);
- спектральная норма матрицы К [1].
В.И. Вершинин в статье "Влияние ошибок весов измерений на результаты уравнивания и оценку точности" в качестве основного показателя степени нарушения строгости уравнивания использует следующий коэффициент:
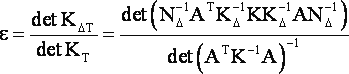 |
(1) |
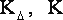 |
- приближенная и точная корреляционные матрицы измерений; |
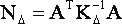 |
- матрица нормальных уравнений приближенного уравнивания. |
Путём некоторых математических преобразований автор выводит другую формулу, аналогичную (1), но без учёта отношения приближённой и точной оценок дисперсии единицы веса µ²d/µ²:
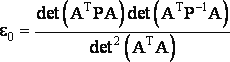 |
(2) |
На основании формулы (2) автор делает важный вывод, что при использовании лишь необходимых измерений любые ошибки в весах измерений не влияют на значение коэффициента e0. Дальнейшее исследование автор строит на соотношении числа необходимых и избыточных измерений [2].
С.Г. Могильный в статье "Метод определения необходимой точности весов измерений" предлагает другой алгоритм исследования - искать общую меру искажения всей совокупности весов уравновешиваемых измерений. Одна из возможных таких мер, по мнению автора, может быть получена при рассмотрении общёй арифметической середины.
Для выявления общего свойства совокупностей весов, которые приводят к одним и тем же искажениям результатов уравновешивания, Могильный переходит к геометрической форме и рассматривает совокупность весов как вектор в n-мерном пространстве.
Выполняя исследования в этой области, автор приходит к выводу, что искажение результата уравновешивания может определяться tg ф (ф - угол между вектором точных и приближённых весов), который и следует принять за меру искажения совокупности весов [3].
Мои достижения
На основании изученных материалов я хочу попытаться предложить иной метод исследования влияния ошибок весов измерений на результаты уравнивания и оценку точности сетей полигонометрии.
Исследования я провожу на программе Mathcad на примере несложного хода полигонометрии ломаной формы. В этом ходе известны координаты исходных пунктов А и В, дирекционные углы aАС и aВD и средние квадратические ошибки измерения длин линий и углов - 5 мм и 2", соответственно.
Данная сеть уравнивается параметрическим способом и получаются матрицы А, Р и вектор L, используемые в дальнейших расчётах. Матрица А - матрица коэффициентов уравнений поправок или матрица частных производных (рис. 1), матрица Р - матрица весов и вектор L - вектор свободных членов уравнения поправок (рис. 2).
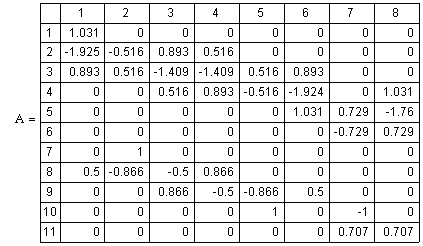 |
| Рисунок 1 - Матрица коэффициентов уравнений поправок |
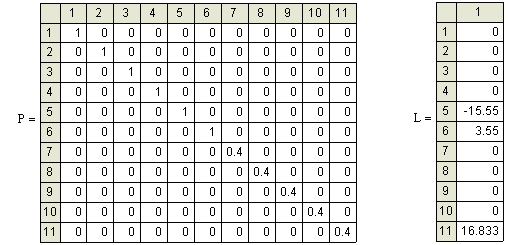 |
| Рисунок 2 - Матрица весов и вектор свободных членов уравнения поправок |
Исследовать влияние ошибок весов измерений я предлагаю используя матрицу ошибочных весов Psl (рис. 4), которая образуется путём сложения истиной матрицы весов Р и матрицы ошибок к весам dР (рис. 3), сгенерированных случайным образом:
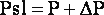 |
(3) |
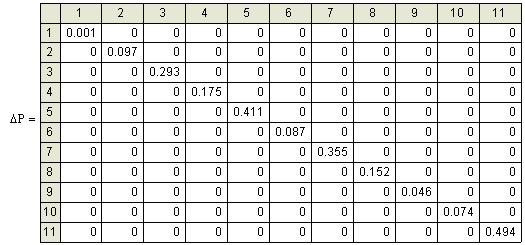 |
| Рисунок 3 - Матрица ошибок к весам |
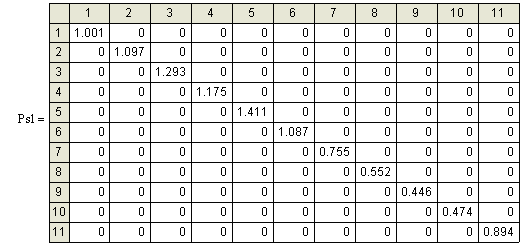 |
| Рисунок 4 - Ошибочная матрица весов |
Используя формулу нахождения вектора-решения из параметрического способа уравнивания можно найти вектор-решение для нашей сети двумя способами: по истиной матрице весов и по ошибочной. Для достижения цели исследования необходимо найти различие этих двух векторов, т.е. узнать, насколько введённые ошибки сместят истинные значения (рис. 5):
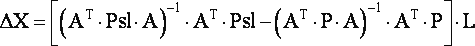 |
(4) |
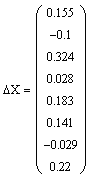 |
| Рисунок 5 - Вектор искажений результатов из-за ошибок весов |
Чтобы оценить влияние ошибок весов и установить некоторые закономерности их распределения, необходимо знать дисперсии этих ошибок, т.е. разброс относительно некоторого среднего значения.
Известно, что дисперсия нескольких функций случайных величин характеризуется ковариационной матрицей, поэтому найдём ковариационную матрицу ошибок результатов из-за ошибок весов. Для этого применим к формуле (4) обобщённую теорему оценки точности и заменим ковариационную матрицу свободных членов KL на обратную матрицу весов Р¯¹. Такую замену можно объяснить следующим образом: известно, что KL совпадает с ковариационной матрицей измеренных значений Ky, которая вычисляется по формуле (5):
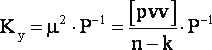 |
(5) |
Как видно из формулы (5) ошибка единицы веса µ зависит от весов измерений. Следовательно, учитывать µ в расчётах является не рациональным. Поэтому проанализируем последующие вычисления. Далее мы будем вычислять ковариационные матрицы истинных значений, поправок и другие, в которых также присутствует общий множитель µ. Мы будем находить отношения этих матриц, следовательно, множитель µ в отношении даст нам 1 и влиять не будет. Таким образом, без учёта µ, формула для нахождения ковариационной матрицы ошибок результатов из-за ошибок весов будет выглядеть следующим образом:
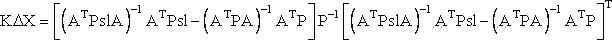 |
(6) |
Преобразуем эту формулу:
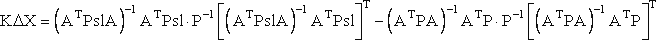 |
(7) |
Проанализируем полученную формулу (7). Здесь уменьшаемое является формулой для вычисления ковариационной матрицы поправок Kpr, а вычитаемое - для вычисления ковариационной матрицы истинных значений координат. Можно также провести некоторые преобразования Мх:
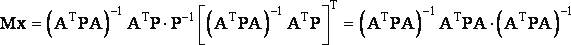 |
(8) |
Нетрудно заметить, что множитель АTРА·(ATPA)-1 является единичной матрицей и, следовательно, формула (8) преобразуется в более простую:
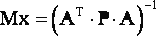 |
(9) |
Матрицы Kpr, Мх и КdХ представлены на рисунках 6, 7 и 8.
 |
| Рисунок 6 - Ковариационная матрица поправок |
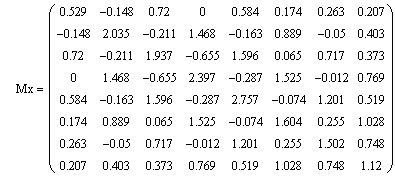 |
| Рисунок 7 - Ковариационная матрица истинных значений координат |
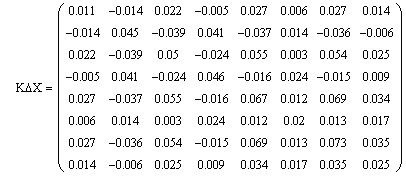 |
| Рисунок 8 - Ковариационная матрица ошибок результатов из-за ошибок весов |
Вернёмся к матрице КdХ - ковариационной матрице ошибок результатов из-за ошибок весов. Диагональные элементы этой матрицы - дисперсии ошибок результатов, или средние квадратические отклонения в квадрате - a².
Таким образом, дальнейшие вычисления будут сводиться к тому, чтобы найти какую долю составляет отклонение из-за ошибок веса в общей ошибке. Для этого необходимо найти отношение диагональных элементов матрицы КdХ и матрицы Мх - ковариационной матрицы истинных значений координат, диагональные элементы которой - средние квадратические отклонения истинных значений координат в квадрате.
Для упрощения вычислений выберем диагональные элементы матриц КdХ и Мх в векторы-столбцы kdx и mx (рис. 9). Отношение соответствующих элементов этих векторов представлено на рисунке 9.
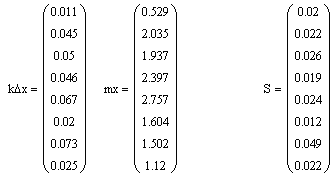 |
| Рисунок 9 - Векторы диагональных элементов матриц КdХ и Мх и вектор отношений их элементов |
Теперь из полученных значений надо найти максимальное. В данном случае это значение 0,049.
Конечным результатом исследования должен стать график, который бы показывал зависимость максимальной ошибки из-за веса от угла между истинным вектором весов и ошибочным в n-мерном пространстве весовых векторов.
Из формул векторной алгебры известно, что вычислить косинус угла между истинным весовым вектором и любым другим можно по формуле (10):
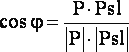 |
(10) |
Для того чтобы построить график, я сгенерировала совокупность случайных векторов весов, исказив истинный вектор веса на разные величины (от 0,05 до 100). Выполнив вычисления по предложенным выше формулам, я получила матрицу gr (рис. 10), первый столбец которой - величина угла между истинным вектором весов и ошибочными в градусах (изменяется приблизительно от 0° до 45°), а второй - значение соответствующей доли ошибки из-за веса в общей ошибке. В этой матрице находятся 90 точек - такое количество я посчитала достаточным для наглядного представления графика.
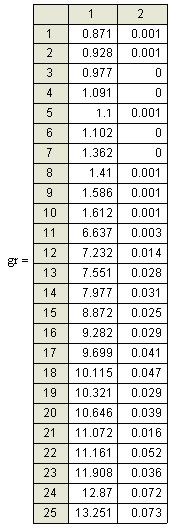 |
| Рисунок 10 - Матрица для построения графика |
Полученный график представлен на рисунке 11.
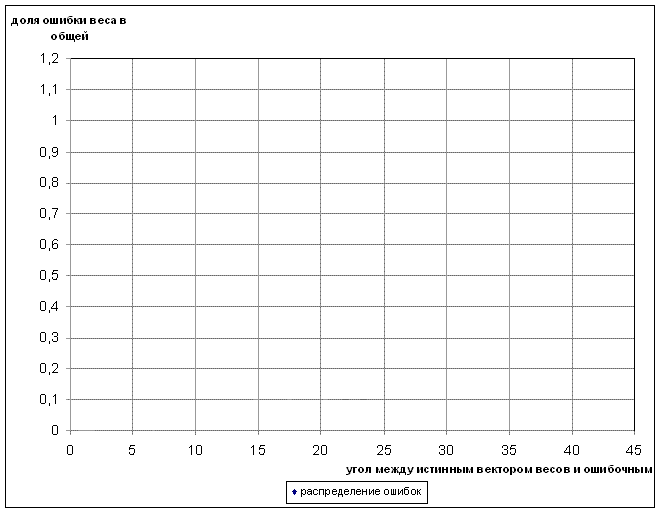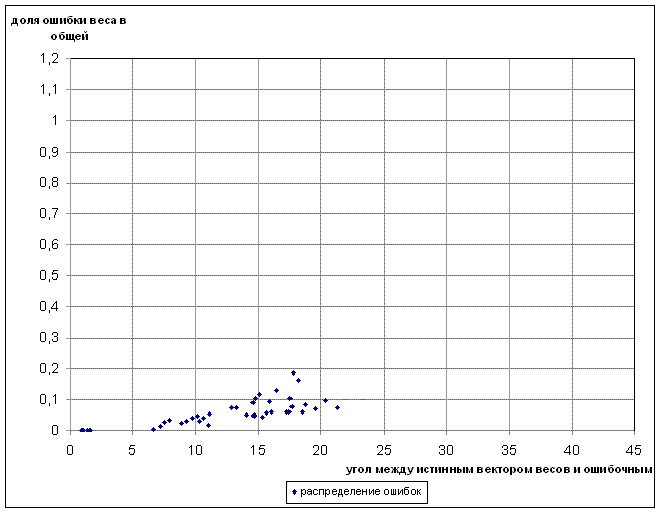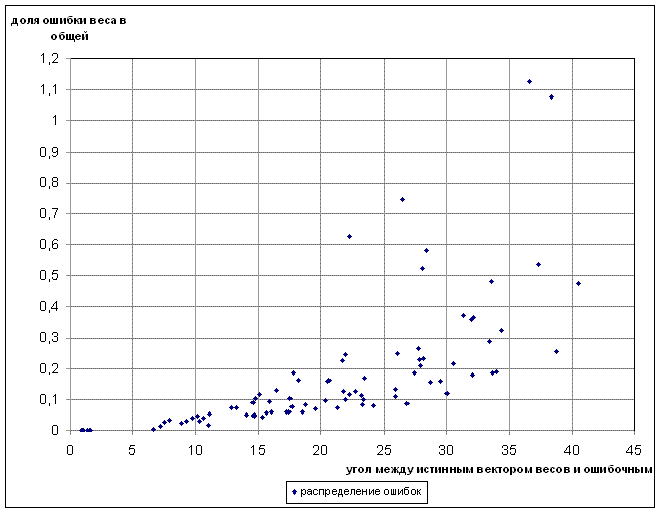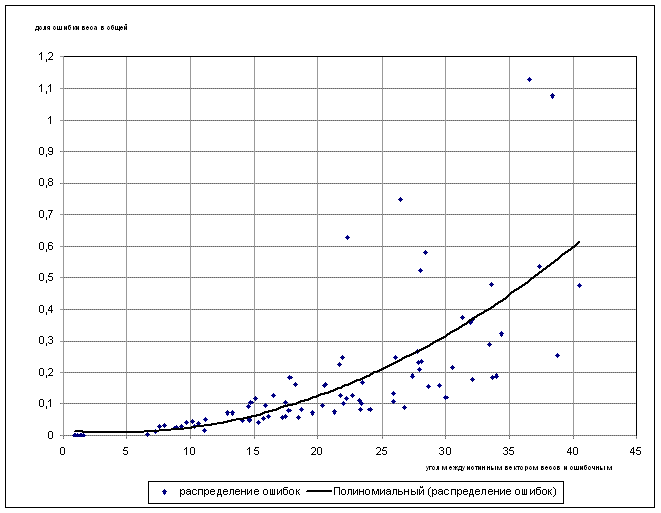 |
Рисунок 11 - График зависимости максимальной ошибки из-за веса от угла между истинным вектором весов и ошибочным
(анимация выполнена в Microsoft GIF Animator: 10 кадров, 5 циклов повторения, размер 102 Kb) |
Как видно из рисунка, график представляет собой совокупность точек. Для наглядности, проведём по этим точкам линию тренда. Теперь стало ясно видно, что доля ошибки из-за веса в общей ошибке возрастает с увеличением угла между истинным вектором весов и ошибочным. Следовательно, чем больше ошибки весов, тем сильнее они искажают результаты уравнивания.
Представим данный график таким образом, чтобы он показывал зависимость максимальной ошибки из-за веса от количества раз, в которое случайный вектор весов может отличаться от истинного. Для этого вычислим, во сколько больше каждый элемент случайных векторов весов соответственных элементов истинного вектора. Затем из полученных значений найдём максимальное и построим искомую зависимость (рис. 12).
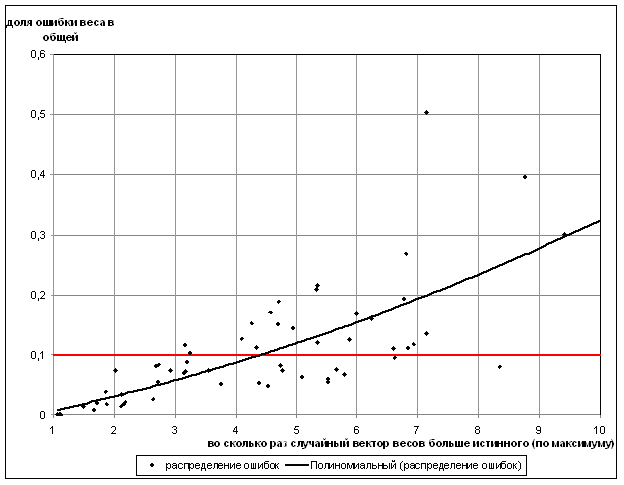 |
| Рисунок 12 - График зависимости максимальной ошибки из-за веса от количества раз, во сколько случайный вектор весов больше истинного |
В изученной мной литературе указывается, что отклонения весов меньше, чем на 10%, не оказывают влияния на результаты уравнивания. Если это действительно так, то, как следует из графика, если в данной сети максимальная ошибка элемента вектора весов искажает соответственный элемент истинного вектора меньше, чем в 4,4 раза, то ошибки вектора весов на результаты уравнивания и оценку точности влиять не будут.
Направление дальнейших исследований
Дальнейшую свою цель я вижу в поиске путей нахождения некоторого предельного значения доли ошибки, которое бы оказывало минимальное влияние на результаты уравнивания и оценку точности сетей полигонометрии. А также я планирую исследовать влияние ошибок весов на уравнивание сетей полигонометрии различной формы и конфигурации и сделать возможные общие заключения.
Литература
1. Скейвалас И.М. Обобщённая оценка точности результатов уравнивания // Изв. вузов. Сер. Геодезия и аэрофотосъёмка. - 1984. - №2. - С. 13-17;
2. Вершинин В.И. Влияние ошибок весов измерений на результаты уравнивания и оценку точности // Геодезия и картография. - 2000. - №6. - С. 17-22;
3. Могильный С.Г. Метод определения необходимой точности весов измерений // Инженерная геодезия. Респ. межвед. научн.-техн. сб. - 1972. - вып. 12. - С. 44-50.
 |
Автор
Елена Захарова |
© ДонНТУ 2008 Захарова
 Автобиография
Библиотека
Ссылки
Отчёт о поиске
Как отдыхают студенты
Автобиография
Библиотека
Ссылки
Отчёт о поиске
Как отдыхают студенты