MULTIBAND SIGNAL PROCESSING BY USING NONUNIFORM SAMPLING AND
ITERATIVE UPDATING OF AUTOCORRELATION MATRIX
Author: M. Greitans
Source: Proceedings of the 2001 International Conference on Sampling Theory and Application, May 13-17, 2001, Orlando, Florida, USA, pp. 85-89
Full Version: http://www.edi.lv/dasp-web/dasp-papers/Greitans_sampta01.pdf
Abstract
The approach to multiband signal processing is considered.The method discussed in this paper is based on nonuniform sampling, Minimum Variance filter and iterative updating of autocorrelation matrix. That allows to process a multiband signal even if the number of known signal samples is less than equivalent of Nyquist criterion for uniform sampling. The proposed approach of multiband signal processing is suitable for spectral analysis, estimation of power spectral density and autocorrelation functions as well as for signal reconstruction. The information about the limits of the signal's subband frequencies gives the possibility to reconstruct the waveform of each signal part separately. It means that the suggested multiband signal processing method provides also some capability of signal subband filtering. The performance of the method is illustrated by the conjoint GSM900 and GSM1800 signal processing example.
1 Introduction
Often the multiband signal processing is based on calculation of special sampling series in accordance with the signal spectral region location [1]. The possibility of achieving the minimum sampling density (equivalent of the Nyquist rate for uniform sampling) depends on possibility to tessellate frequency space by a group of translations. In general, the calculated sampling instants of a multiband signal are spaced nonuniformly therefore any changes of the signal subband limits leads to the necessity to recalculate signal sampling series.
This paper discusses the multiband signal processing if arbitrary nonuniform sampling series is used. If it has a quality of frequency aliasing suppression [2], then there are no special requirements regarding the exact values of the sampling moment. Only two general conditions should be considered – the maximum gap between two known samples and the sampling density should be conformed to the equivalent signal bandwidth [3, 4].
Traditionally, signal processing methods take into account only one parameter of signal power spectral density (PSD) function P(f), namely, the frequency boundaries of the spectrum. If such limits do exist, the signals are called band-limited signals. The PSD function of a multiband signal consists of several separate frequency regions. It can take different appearance within these spectral subbands. One way to characterize the form of PSD is to use the equivalent bandwidth of the band-limited signal defined as [3]
 (1) (1)
It is obvious that for real applications the value of the equivalent signal bandwidth is usually smaller than the actual signal bandwidth. Therefore, as it is shown in [4], nonuniform sampling allows to process signals employing less signal samples than it is required by the Nyquist criterion in conformity with the cumulative signal bandwidth.
2 Processing method
The existence of several subbands in a multiband signal spectrum determines the necessity for developing of a special processing method taking into account the information about the boundaries of the signal frequency regions. The suggested multiband signal processing approach is based on the Minimum Variance method [3, 5]. The basic idea of this method is to minimize the variance of the narrowband filter output signal. The frequency response of this filter adapts to the input signal spectral components on each frequency of interest. The variance of the output process is determined as:
 (2) (2)
where a is the vector of filter coefficients, while R is the signal autocorrelation matrix. In addition, filter coefficients should guarantee that on the frequency f0 the gain of the filter response will be one. This condition could be described as:
 , (3) , (3)
where  . On the other
hand, the expression (3) means that a sinusoid at frequency f0
passes through the filter designed for this frequency without
distortion. It is shown in [6] that the coefficients of the filter
under condition (3) for the frequency f0 are determined as: . On the other
hand, the expression (3) means that a sinusoid at frequency f0
passes through the filter designed for this frequency without
distortion. It is shown in [6] that the coefficients of the filter
under condition (3) for the frequency f0 are determined as:
 (4) (4)
Taking into account expression (3), the output s of the designed filter
 , (5) , (5)
can be interpreted also as a complex spectral value (analogous of Fourier transform value) of signal x on the frequency f0 [7]. Therefore the PSD value of the signal on this frequency can be calculated as
 (6) (6)
For the multiband signal processing task, each
signal subband should be covered by the set of such filters. The
distance between filter frequencies can be chosen equal to the
frequency step of Discrete Fourier transform  , where
, where  is the length
of the signal to be analyzed. According to expression (4) the
filter coefficients depend on the signal autocorrelation matrix.
Usually the values of this matrix are not known a priori. Therefore
the estimates of autocorrelation matrix values should be calculated
from known signal samples. The traditional approach for obtaining
correlation matrix is based on averaging of the mutual products
of signal samples. It is not applicable in the nonuniform sampling
case, because the time intervals between sampling points are not
distributed regularly. Instead of that the cross-relation of signal's
autocorrelation and power spectral density functions is the length
of the signal to be analyzed. According to expression (4) the
filter coefficients depend on the signal autocorrelation matrix.
Usually the values of this matrix are not known a priori. Therefore
the estimates of autocorrelation matrix values should be calculated
from known signal samples. The traditional approach for obtaining
correlation matrix is based on averaging of the mutual products
of signal samples. It is not applicable in the nonuniform sampling
case, because the time intervals between sampling points are not
distributed regularly. Instead of that the cross-relation of signal's
autocorrelation and power spectral density functions
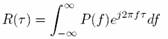 (7) (7)
is employed for R calculation [8]. Moreover,
the expression (7) allows to take into account also the known
values of signal spectral subbands, because the integration should
be done only in the defined frequency regions. The most popular
and simple way to obtain P(f)
estimate from signal samples in the nonuniform sampling case is
to use DFT. In accordance with approach described above the spectral
analysis is performed in the fixed set of frequencies f =
[f1; f2; :::fM].
The known signal values x = [x1;
x2; :::xN] are sampled
at defined time instants t = [t1;
t2; :::tN]. Thereby the
values of autocorrelation function can be obtained as:
 (8) (8)
where  and (0)
means that it is zero order estimate of R. Signal autocorrelation
matrix values obtained by (8) are rather rough estimates that
lead to rough estimation of signal complex spectral function values and (0)
means that it is zero order estimate of R. Signal autocorrelation
matrix values obtained by (8) are rather rough estimates that
lead to rough estimation of signal complex spectral function values
 (9) (9)
and PSD function values
 (10) (10)
A special iterative updating algorithm, similar to described in [4, 7], is used to improve the results of processing. According to this algorithm the (i+1)-th order estimate of signal autocorrelation matrix is updated from the i-th order P(i) estimate in the following way
 (11) (11)
Now, using matrix  , the estimates , the estimates  and and  can be calculated using expressions (9)-(10). In effect, an iterative algorithm has been derived. The iteration process (9)-(11) can be stopped when the difference can be calculated using expressions (9)-(10). In effect, an iterative algorithm has been derived. The iteration process (9)-(11) can be stopped when the difference  becomes small.
Although becomes small.
Although  is a positive definite symmetric matrix, it becomes ill conditioned as the number of the known samples increase [9]. In that case, the direct inversion of R^ (i) leads to processing errors. Therefore the expression for obtaining PSD of signal could be derived as is a positive definite symmetric matrix, it becomes ill conditioned as the number of the known samples increase [9]. In that case, the direct inversion of R^ (i) leads to processing errors. Therefore the expression for obtaining PSD of signal could be derived as
 (12) (12)
where matrix d is solution of following matrix equation:
 (13) (13)
The equation (13) could be solved by iterative methods [9, 10], for example, the conjugate gradient method. As it was mentioned above, the vector S can be interpreted as complex spectral values, therefore the inverse DFT could be used to obtain the values of reconstructed signal [7]. If the multiband signal processing task is to perform some subband filtering then for inverse DFT input only certain parts of estimated S values could be exploited.
References
[1] J. R. Higgins, ‘Some gap sampling series for multiband signals", Signal Processing, vol. 12, no. 3, pp. 313-319, 1987.
[2] I. Bilinskis and A. Mikelsons, Randomized Signal Processing, Prentice-Hall, 1992.
[3] S. M. Marple Jr., Digital spectral analysis with applications, Prentice-Hall, 1987.
[4] M. Greitans, “Iterative Reconstruction of Lost Samples Using Updating of Autocorrelation Matrix", in Proc. SampTA'97, Workshop on Sampling Theory & Applications, Aveiro, Portugal, pp. 155-160, Jun. 1997.
[5] S. M. Kay and S. L. Marple Jr., “Spectrum analysis - a modern perspective", Proc. of the IEEE, vol. 69, no. 11, pp. 1525-1578, 1981.
[6] McDonough R. N., “Aplication of the Maximum-Likelihood Method and the Maximum-Entropy Method to Array Processing", Chapter 6 in Nonlinear Methods of
Spectral Analysis, 2nd ed., S. Haykin, ed., Springer-Verlag, New York, 1983.
[7] V. Liepinsh, “An algorithm for estimation of discrete Fourier transform from sparse data", Automatic control and computer sciences, vol. 29, no. 3, pp. 27-41, 1996.
[8] J. S. Bendat, A. G. Piersol, Engineering applications of correlation and spectral analysis, John Wiley & Sons Inc., 1980.
[9] A. K. Jain and S. Ranganath, “Extrapolation algorithms for discrete signals with application in spectral analysis", IEEE Trans. Acoust., Speech, Signal Processing, vol. ASSP-29, no. 4, pp. 830- 845, 1981.
[10] G. H. Golub and C. F. van Loan, Matrix computations, The Johns Hopkins University Press, Baltimore, 1989.
[11] M. Mouly and M. B. Pautet, The GSM System for Mobile Communications, Cell & Sys, 1992.
|

