


Специальность: Электрические сети и системы
Тема магистерской работы: Анализ статической устойчивости электрической системы, в которой генераторы оснащены АРВ сильного действия
Руководитель: Ларин Аркадий Михайлович
Объектом разработок и исследований есть простейшая электрическая система. Нужно исследовать влияние автоматического регулятора возбуждения сильного действия на устойчивость системы.
Цель работы – разработка программного обеспечения по результатам исследований влияния коэффициента усиления, постоянной времени и угла на устойчивость системы.
Разработки выполнялись с использованием знаний полученных из курса «Переходные электромеханические процессы в электрических системах». В соответствии с исходными данными был составлен порядок расчета, описанная его реализация, учитывая особенности задачи. С помощью программного пакета MathCAD расчеты были реализованы. А также были созданные методические указания к программному продукту.
С помощью этой дипломной работы можно продемонстрировать эффективность использования АРВ сильного действия, а также убедиться, что использования ПЕОМ и программного пакета MathCAD, разрешает уменьшить затраты времени на расчеты и повысить их точность.
Автоматическое регулирование возбуждения в настоящее время, как правило, применяется на всех электростанциях (генераторах), присоединенных к электрическим системам. Пересчитаем основные задачи (что относятся к статическим свойствам системы и что рассматриваются с помощью метода малых колебаний), решаемые с помощью регулирования возбуждения:
- повышение границы передающей мощности за счет управления величиной ЭДС генератора и устранения факторов, способных вызвать самораскачивание системы близ границы устойчивости;
- улучшение качества режима системы за счет поддержки напряжения в начале передачи и обеспечения возможно более быстрого затухания малых колебаний, которые возникают в нормальном режиме и неблагоприятно отображаются на качестве работы системы;
- улучшение параметров системы, вчастности, изменение собственной частоты колебаний и устранения возможности резонанса колебаний.
Чтобы регуляторы возбуждения могли удовлетворительно решать вышеперечисленные задачи, необходимо определенным образом подобрать параметры всей системы возбуждения, включая и параметры самых регуляторов. Решения каждой задачи накладывает на выбор параметров системы регулирования свои требования, которые изменяются при изменении схемы и параметров регулированной системы, а также и при изменении его режима.
Задача анализа – проверка устойчивости системы и определения качества переходного процесса при заданных параметрах регулятора и системы;
Задача синтеза – когда, исходя из определенных требований к устойчивости и качества переходного процесса регулированной системы определяется вид регулятора (структурная схема системы регулирования) и его параметры.
В работе рассматривается система, которая состоит из станции, которая работает через передачу (возможно, с промежуточными нагрузками) на шины неизменного напряжения и частоты.
При анализе регулированной системы, ровно как и при синтезе, надо математически описать процессы что в ней происходят, с тем чтобы с решения соответствующих дифференциальных уравнений найти все необходимые коэффициенты, которые характеризуют стойкую работу системы при заданном или чтобы при заданных параметрах проверить, будет ли система устойчивая.
Составление такого уравнения и анализ его свойств для системы регулирования возбуждения сильного действия будет основной целью и задачей дипломной работы.
Для достижения цели работы были поставленные и решенные следующие задачи:
- разработка программного обеспечения для изучения теоретических положений анализа статической стойкости электрических систем с АРВ сильного действия;
- разработка программного обеспечения для выполнения расчетов относительно определения условий статической устойчивости методом малых колебаний;
- исследования электрической системы с АРВ сильного действия;
- разработка методических рекомендаций для создания лабораторной работы по изучению условий статической устойчивости более простой электрической системы с АРВ сильного действия.
Оснащения электрических систем быстродействующими регуляторами возбуждения, заставляет применять этот метод и для исследования стойкости электрических систем.
При этом элементы электрической системы - генераторы с их системами возбуждения, линии электропередачи и нагрузка - рассматриваются как единый объект, устойчивость которого в целом должна быть обеспечена. В результате исследования оказываются требования и к автоматическому регулятору и к самой системе возбуждения, а в отдельных случаях может быть поставлен вопрос и об изменении параметров основного оборудования: генераторов и синхронных компенсаторов.
Метод малых колебаний основанный на исследовании уравнений переходного процесса в рассмотренной системе, причем употребятся не самые уравнения, а их линейное приближение.
Возможность исследования статической устойчивости по линеаризованным уравнением показанная А. М. Ляпуновим, который доказал, что система устойчивая в малом , если устойчиво ее линейное приближение.
Чтобы линеаризировать нелинейные дифференциальные уравнения переходного процесса, нужно:
- допустить, что отклонения координат (независимых переменных) маленькие;
- все нелинейные функции, которые входят у уравнение, разложить в ряды Тейлора в окраинах заданных значений координат (исходного режима):
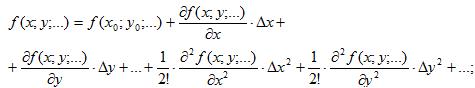
- в разложениях оставить лишь члены, которые содержат отклонение в первых степенях (линейные члены);
- из полученных уравнений исключить уравнение равновесия.
Судить о устойчивости системы можно по знаку действительной части корней характеристического уравнения, которым есть главный определитель полученной системы уравнений. Система устойчивая, если все действительные корни и действительные части комплексных корней мнимые, то есть все корни расположены по левую сторону от мнимой вехе комплексной плоскости. Однако определить корни характеристического уравнения довольно тяжело, так как порядок характеристического уравнения обычно высокий, - пятый и выше. Для этого используют методы, которые разрешают, не определяя корней характеристического уравнения, судить про их расположение на комплексной плоскости. Это критерии Гурвица, Раусса, Михайлова, метод выделения областей устойчивости в плоскости одного или двух параметров (D-разбиения) и т.д.
Схема простейшей электрической системы, относительно которой будет изучаться статическая устойчивость, показана на рис.1. Система имеет автоматическое регулирование возбуждения, которое состоит из трех элементов, параметры которых представленные на рис.1.
Регулятор выполнен с помощью электрических элементов (отдельные элементы обведены пунктиром).
- на выходе регулятора пропорционально отклонению напряжения , которое измеряется на измерительном элементе. Измерительный элемент имеет мостовую схему с нелинейным элементом в левом верхнем плече. Нелинейность подобрана так, что при
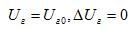
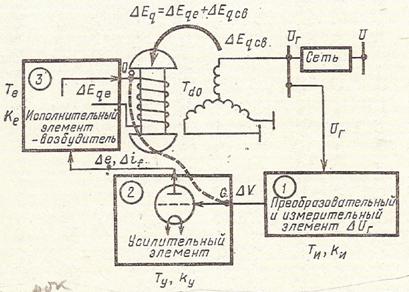
Рисунок 1. Схема простейшей электрической системы, которая имеет регулятор возбуждения сильного действия, представленное тремя элементами (1, 2, 3 ): - - - обратная связь, в результате действия которой 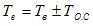 .
.
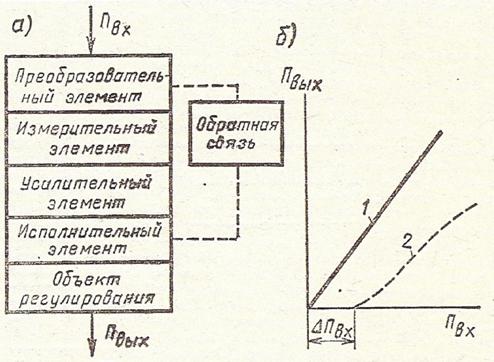
Рисунок 2. Функциональная схема регулятора и его действие: а - структура регулятора; б - изменение исходного параметра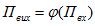 при сильном регулировании без зоны бесчувственности (1) и с зоной бесчувственности
при сильном регулировании без зоны бесчувственности (1) и с зоной бесчувственности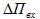 (2).
(2).
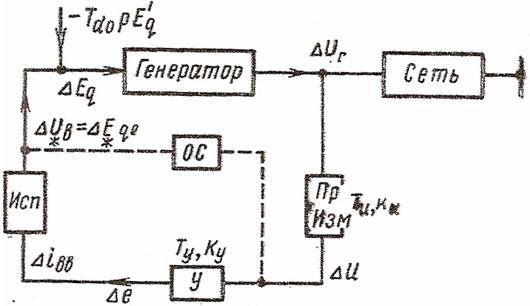
Рисунок 3. Структурная схема регулированной системы, показанной на рис.1
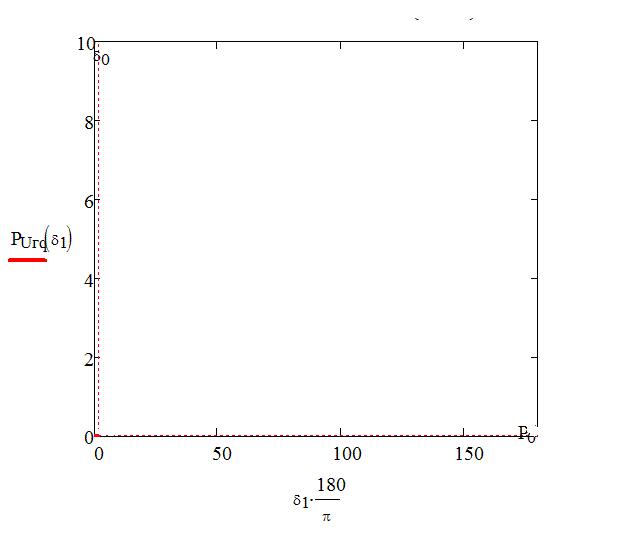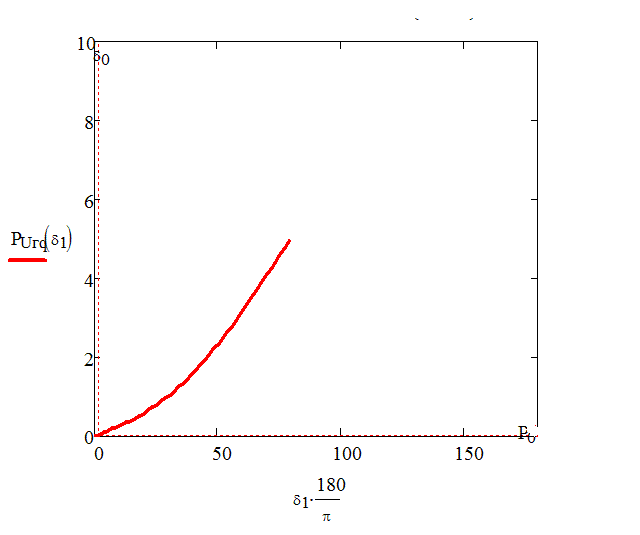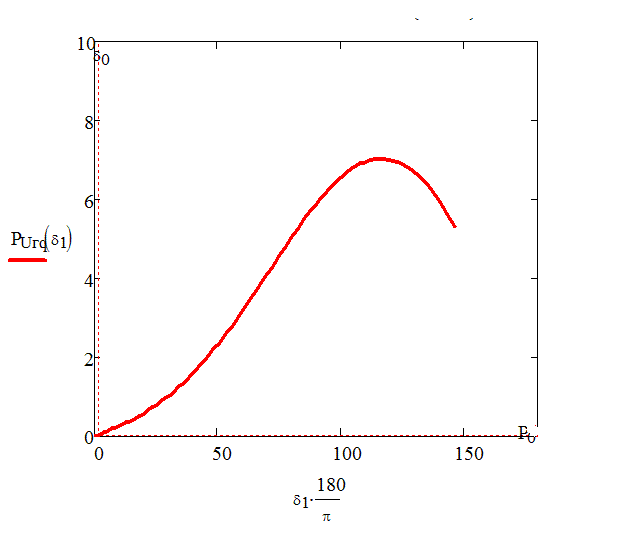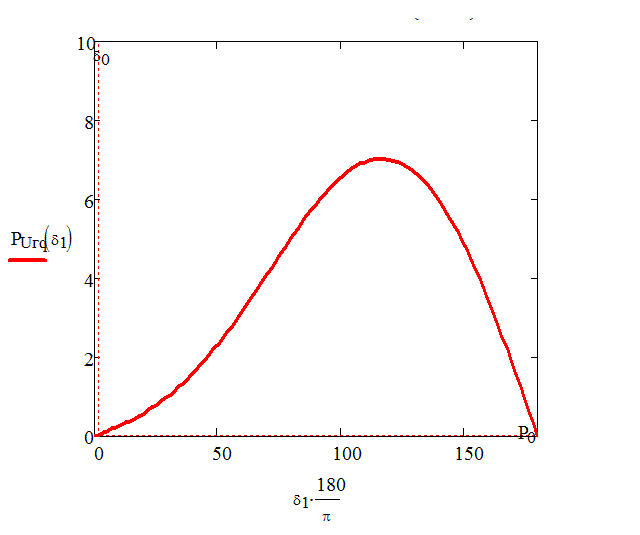
Рисунок 4 -Угловая характеристика генератора с АРВ сильного действия (в данной анимации использовано 10 кадров, количество циклов – 10, размер – 17 КБ)
Исходные дифференциальные уравнения
При исследовании устойчивости электрических систем обычно рассматриваются электромеханические и электромагнитные переходные процессы в электрической системе. К ним в первую очередь относятся переходные процессы, связанные с относительным перемещением роторов синхронных машин – электромеханические процессы и переходные процессы в обмотке возбуждения генератора и самому возбудителю – электромагнитные процессы. Эти переходные процессы в первом приближении описываются следующими дифференциальными уравнениями: Уравнения относительного движения ротора генератора:
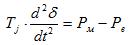 (1)
(1)
где-постоянная инерции генератора (рад.);
-механическая мощность турбины (в относительных единицах);
-электрическая мощность генератора (в относительных единицах);
Укажем, что при решении практических задач удобные другие формы записи этого уравнения, а именно:
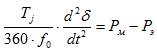 (2)
(2)
где постоянная инерции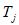 и время t выраженные в сек, а угол
и время t выраженные в сек, а угол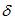 – в градусах, и
– в градусах, и
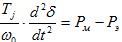 (3)
(3)
где - постоянная инерции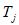 и время t выраженные в сек, а угол
и время t выраженные в сек, а угол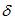 – в рад. Эти уравнения могут быть получены с уравнения (1) путем соответствующих подстановок. Уравнения переходного процесса в обмотке возбуждения генератора:
– в рад. Эти уравнения могут быть получены с уравнения (1) путем соответствующих подстановок. Уравнения переходного процесса в обмотке возбуждения генератора:
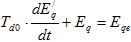 (4)
(4)
где 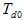 – постоянная времени обмотки возбуждения генератора при разомкнутой обмотке статора (рад. или сек),
– постоянная времени обмотки возбуждения генератора при разомкнутой обмотке статора (рад. или сек),
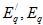 – продольные ЭДС соответственно за переходными и синхронным реактивными сопротивлениями;
– продольные ЭДС соответственно за переходными и синхронным реактивными сопротивлениями;
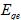 – ЭДС постоянного режима, которое равняется в относительных единицах напряжению возбудителя,
– ЭДС постоянного режима, которое равняется в относительных единицах напряжению возбудителя,
t – время (рад. или сек);
Уравнения переходного процесса в возбудителе:
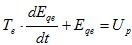 (5)
(5)
где 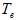 – постоянная времени обмотки возбуждения возбудителя (рад. или сек);
– постоянная времени обмотки возбуждения возбудителя (рад. или сек);
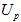 – постоянное значение напряжения возбудителя, которое равняется в относительных единицах напряжению на выходе регулятора.
– постоянное значение напряжения возбудителя, которое равняется в относительных единицах напряжению на выходе регулятора.
Это уравнение может быть получено ниже приведенным путем.
Для возбудителя (см. рис. 1) связь между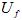 в его обмотке возбуждения (без учета насыщения) может быть представлена в следующем виде:
в его обмотке возбуждения (без учета насыщения) может быть представлена в следующем виде:
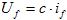 (6)
(6)
Для обмотки возбуждения возбудителя можно записать:
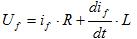
или в операторной форме
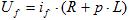 (7)
(7)
Уберём из (1.6) и (1.7) ток возбуждения и обозначим
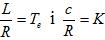 ,
,
Получим
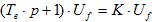
что в обычной форме и отвечает уравнению (5).
Уравнения идеального автоматического регулятора напряжения сильного действия, которое мгновенно изменяет напряжение на ОВВ, пропорционально отклонению напряжения на зажимах генератора:
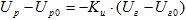 (8)
(8)
Где 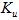 – коэффициент усиления (регулирования) регулятора.
– коэффициент усиления (регулирования) регулятора.
Система приведенных уравнений содержит шесть переменных: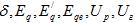
Дополнительные уравнения, которые связывают их между собою, могут быть получены из векторной диаграммы генератора рис.4:
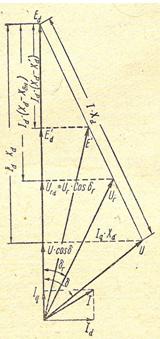
Рисунок 4. Векторная диаграмма синхронной машины с неявно выраженными полюсами.
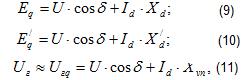
Где
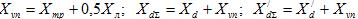
Определив с (9) ток 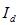 и подставив его у уравнение (10) и (11), запишем отсутствующие уравнения:
и подставив его у уравнение (10) и (11), запишем отсутствующие уравнения:
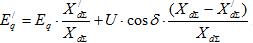 (12)
(12)
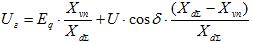 (13)
(13)
Таким образом, для исследования системы, которая содержит генератор с АРВ сильного действия нужно иметь систему из шести уравнений. С учетом выполненного анализа эта система исходных дифференциальных уравнений может быть записана в следующем виде если не учитывать влияние демпфирования.
Запишем шесть уравнений:
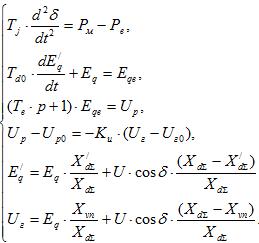 (14)
(14)
Для генератора с автоматическим регулятором возбуждения, которое реагирует на отклонение напряжения, при работе через линию электропередачи на шины постоянного напряжения, могут быть записанные следующие уравнения переходного процесса:
уравнения относительного движения ротора генератора:
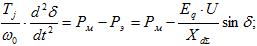 (15)
(15)
уравнения переходного процесса в роторе генератора:
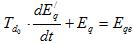 (16)
(16)
уравнения переходного процесса в возбудителе:
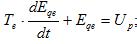 (17)
(17)
уравнение регулятора:
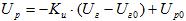 (18)
(18)
где 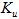 – коэффициент усиления регулятора
– коэффициент усиления регулятора
Знак минус перед 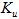 поставлен потому, что возрастание
поставлен потому, что возрастание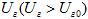 должно сопровождаться уменьшением
должно сопровождаться уменьшением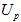 , а снижения
, а снижения 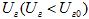 – увеличением
– увеличением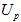 .
.
Для исследования полученной системы уравнений ее необходимо дополнить еще двумя, так как уравнений всего 4, а переменных 6: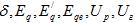 .
.
Отсутствующие уравнения могут быть получены из векторной диаграммы генератора (см. рис. 4):
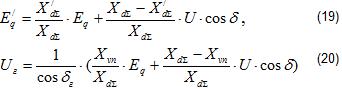
Последнее уравнение можно упростить, приняв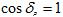 .
.
При этом:
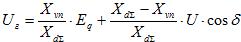
Среди приведенных выше дифференциальных уравнений переходного процесса, рассмотренных при анализе устойчивости электрической системы, уравнения движения ротора генератора нелинейно, так как выражение электрической мощности есть синусоидальной функцией угла. Это обстоятельство, за исключением частных случаев не разрешает найти решения, которое описывает переходный процесс в системе, в общем виде.
Поэтому для определения условий статической устойчивости, то есть устойчивости при маленьких смещениях параметров режима, исследования проводятся на основании линеаризованных уравнений, полученных путем линеаризации исходных нелинейных дифференциальных уравнений.
Линеаризированные уравнения.
Соответственно уравнениям (15) – (21) линеаризированные уравнения, записанные для малых возмущений в дифференциальной форме, имеют такой вид:
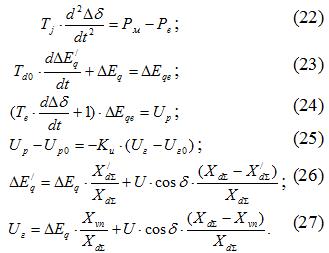
После осуществления замены 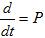 , получим соответствующую систему линейных уравнений записанных в операторном виде.
, получим соответствующую систему линейных уравнений записанных в операторном виде.
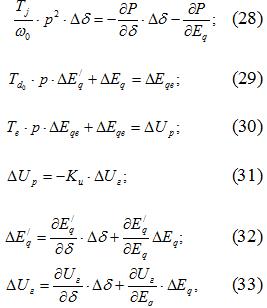
где
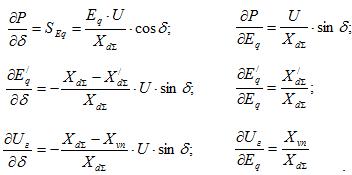
Рассмотрим процессы, которые происходят при регулировании автоматическим регулятором возбуждения сильного действия. Исходя из структурной схемы (рис.3) регулятора, запишем основные соотношения, которые характеризуют его работу.
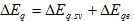 (34)
(34)
Первая составляющая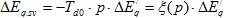 , обусловленная процессами, которые происходят непосредственно в генераторе, отображает влияние реакции якоря.
, обусловленная процессами, которые происходят непосредственно в генераторе, отображает влияние реакции якоря.
Вторая составная
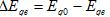
или
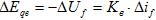 (35)
(35)
отображает изменения тока возбуждения. Это изменение обусловленная изменением ЭДС, приложенной к обмотке возбуждения возбудителя и в свою очередь зависимой от действия регулятора возбуждения (рис. 1). Очевидно, что
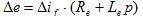
откуда
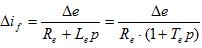 (36)
(36)
Подставляя (36) в (35), получим
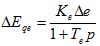 (37)
(37)
где 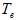 – эквивалентная постоянная времени возбудителя, определенная с учетом обратной связи;
– эквивалентная постоянная времени возбудителя, определенная с учетом обратной связи;
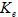 – коэффициент усиления;
– коэффициент усиления;
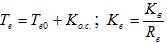
Дале, учитывая, что усилитель есть инерционным элементом с постоянной времени 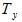 и коэффициентом усиления
и коэффициентом усиления 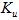 запишем:
запишем:
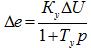 (38)
(38)
Рассматривая преобразовальний и измерительный элементы приблизительно как одно звено с постоянной времени 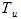 и коэффициентом усиления
и коэффициентом усиления 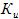
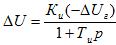 (39)
(39)
Подставляя (39) в (38) и потом в (37), получим
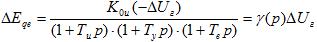 (40)
(40)
где 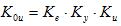 – коэффициент усиления системи
– коэффициент усиления системи
В постоянном режиме 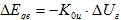 , где
, где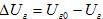 . Отсюда, с учетом (35), можно определить коэффициент усиления:
. Отсюда, с учетом (35), можно определить коэффициент усиления:
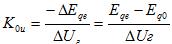
тут
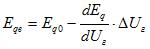
значит
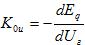
Характеристическое уравнение.
Запишем уравнение движения системы в более компактной форме:
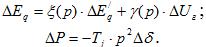
В этих уравнениях имеем пять неизвестных 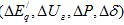 . Выразим прирост мощности
. Выразим прирост мощности 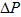 через приросты ЭДС.
через приросты ЭДС. 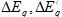 , и прирост напряжения
, и прирост напряжения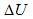 , получим таким образом, еще три уравнения.
, получим таким образом, еще три уравнения.
Прирост мощности 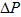 имеет вид:
имеет вид:
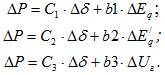
Значения 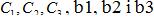 будут следующими:
будут следующими:
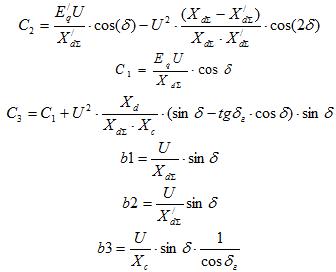
где
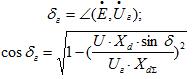
После несложных преобразований будем иметь три уравнения:
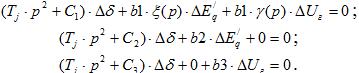
Определитель системы этих трех уравнений – это и есть характеристический детерминант.
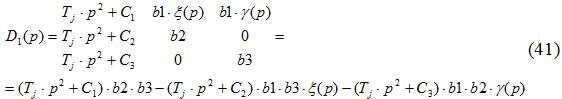
Для того чтобы получить характеристическое уравнение, можно сделать следующее: значение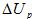 с (31) подставить в (30); значение
с (31) подставить в (30); значение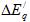 из полученного уравнения, а также
из полученного уравнения, а также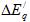 с (32) и
с (32) и 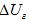 с (33) подставить в (29); составить с (28) и уравнения, которые вышло, определитель и раскрыть его.
с (33) подставить в (29); составить с (28) и уравнения, которые вышло, определитель и раскрыть его.
Получено харатеристичне уравнения четвертого порядка
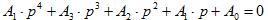 (42)
(42)
запишем в следующем виде:
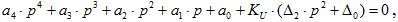
где
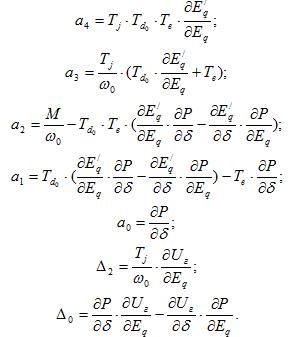
Подставляя в 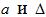 значения частиц производных и вводя новые обозначения, получим
значения частиц производных и вводя новые обозначения, получим
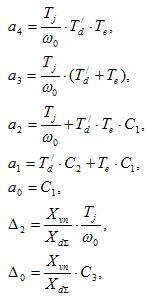 (44)
(44)
где
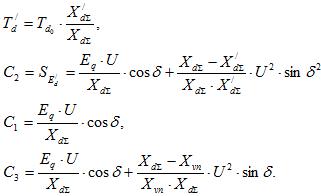
Правая часть характеристического уравнения (43) определяет устойчивость нерегулированной системы (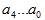 – коэффициенты характеристического уравнения, которые не зависят от регулирования нарушения), а вторая его часть есть математическим отображением влияния автоматического регулирования нарушения (
– коэффициенты характеристического уравнения, которые не зависят от регулирования нарушения), а вторая его часть есть математическим отображением влияния автоматического регулирования нарушения (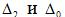 единичные добавки к соответствующим коэффициентам характеристического уравнения, пропорциональные коэффициенту усиления регулятора).
единичные добавки к соответствующим коэффициентам характеристического уравнения, пропорциональные коэффициенту усиления регулятора).
1.Регулирование сильного действия (без зоны бесчувственности) расширяет область стойкой работы и разрешает работать при углах, больших 90°. Предельный угол оказывается тем более, чем меньше постоянная времени возбудителя. При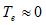 предельный угол стойкой работы определяется условием
предельный угол стойкой работы определяется условием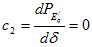 .
.
2. Чем меньше постоянная времени возбудителя 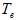 , тем меньше оказывается максимальный возможный коэффициент усиления (рис. 4). Это означает, что выбирая такие большие коэффициенты усиления, при которых напряжение генератора поддерживается неизменным, нельзя обеспечить его роботу с большими предельными углами. Если отказаться от жесткой поддержки напряжения, допуская его снижение с возрастанием нагрузки, то устойчивая работа может быть обеспечена при углах порядка 90° и даже более (рис. 5,б).
, тем меньше оказывается максимальный возможный коэффициент усиления (рис. 4). Это означает, что выбирая такие большие коэффициенты усиления, при которых напряжение генератора поддерживается неизменным, нельзя обеспечить его роботу с большими предельными углами. Если отказаться от жесткой поддержки напряжения, допуская его снижение с возрастанием нагрузки, то устойчивая работа может быть обеспечена при углах порядка 90° и даже более (рис. 5,б).
В простейшем регуляторе сильного действия может обеспечиваться работа при хорошей поддержке напряжения, но тогда устойчивость поднимается при углах, меньших 90°. Обеспечить роботу при углах 90° или нескольких больших можно при худшей поддержке напряжения. Предельная передаваемая мощность оказывается при этом близкая к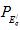 , то есть к максимуму мощности, определенного при постоянности
, то есть к максимуму мощности, определенного при постоянности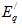 . В упрощенных расчетах генераторы, обеспеченные регуляторами возбуждения сильного действия, вводятся в схему замещения реактивным сопротивлением
. В упрощенных расчетах генераторы, обеспеченные регуляторами возбуждения сильного действия, вводятся в схему замещения реактивным сопротивлением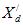 и приложенной за ним е.д.с.
и приложенной за ним е.д.с.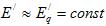 .
.
1. Переходные процессы в системах электроснабжения: Учебник / В. Н. Винославский, Г.Г. Пивняк, Л.И. Несен и др.; Под ред. В. Н. Винославского. – К.: Выща шк. Головное изд-во, 1989. – 422 с.: ил.
2. Методические указания к лабораторным работам по электромеханическим переходным процессам в электрических системах (для студентов специальностей 1001, 1002, 1004.01) / Сост.: Г. Г. Рогозин, А. М. Ларин, Н. Г. Пятлина. – Донецк: ДПИ, 1990. – 48 с.
3. Переходные электромеханические процессы в электрических системах: Учеб. для электроэнергет. спец. вузов. – 2-е изд., перераб. и доп. В. А. Венников / М.: Высш. шк., 1970. – 472 с., ил.
4. Статическая устойчивость электрических систем с синхронными машинами, снабженными автоматическими регуляторами возбуждения.:Лекции / М. Н. Розанов – М. 1959.
5. Переходные электромеханические процессы в электрических системах: Учеб. для электроэнергет. спец. вузов. – 4-е изд., перераб. и доп. / В. А. Венников / М.: Высш. шк., 1985. – 536 с., ил.
6. Жданов П. С. Статическая устойчивость сложных электрических систем. – М.: 1940,
7. Ульянов С. А. Электромагнитные переходные процессы. – М.: Энергия, 1970, 518с.
8. Кафедра ЭСИС- разработка автоматизированной системы управления электрическими системами http://etf.donntu.ru
9. Методы расчетов предельных по статической устойчивости режимов энергосистем http://referats.allbest.ru/programming/103021.html
10. РД 34.20.577 Методические указания по определению устойчивости энергосистем. Литкенс И.В., Васин В.П. Работа электрических систем с АРВ сильного действия вблизи границы области устойчивости. "Электричество", 1968, № 7. 57. Автоматические регуляторы возбуждения. Под ред. Г.Р.Герценберга. http://docyment.ru/doc/5933.htm