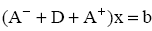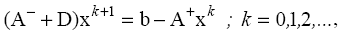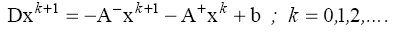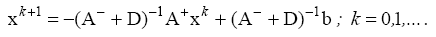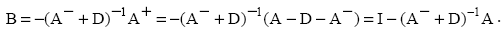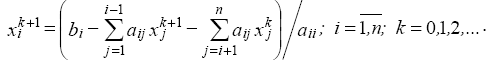|
Автореферат
"Параллельные методы
решения систем
линейных
алгебраических уравнений на вычислительном кластере"
ВВЕДЕНИЕ
На
сегодняшний день производительность вычислительных систем во
многом увеличивается не столько за счет увеличения частоты
работы устройств, сколько за счет привлечения параллельной
обработки [1-3]. Данный процесс затрагивает как создание
аппаратных средств (процессоры с несколькими АЛУ,
коммуникационное оборудование для многопроцессорных систем и
т.д.), так и разработку эффективных алгоритмов для различных
параллельных платформ. Современные параллельные системы
весьма дороги и используются для решения задач, требующих
больших вычислительных ресурсов: предсказания погоды и
климата, построения полупроводниковых приборов, исследования
генома человека и т.д.
Как бы то ни было,
существует возможность создания достаточно дешевой и
относительно эффективной параллельной системы на базе
обычных компьютеров, соединенных при помощи
коммуникационного оборудования и, таким образом, образующих
один вычислительный ресурс. Такие системы называются
кластерами и относятся к классу параллельных систем с
распределенной памятью [1,3]. Узким местом кластеров
является то, что для взаимодействия отдельных узлов
привлекается наиболее распространенное и дешевое
коммуникационное оборудование (Fast Ethernet), которое
использует общую среду передачи данных и обладает не очень
большой пропускной способностью (в сравнении со скоростью
обработки данных современными процессорами). Поэтому круг
задач, решаемых на подобных системах, ограничивается
задачами с небольшим числом обменов по сравнению с
количеством вычислений. Неоспоримым преимуществом подобных
систем является их относительная дешевизна и фактическое
наличие больших компьютерных классов во многих учебных
заведениях. Для программирования подобных систем применяются
системы передачи сообщений, в которых отдельные компьютеры
взаимодействуют посредством передачи и приема данных.
На сегодняшний день
наиболее популярным стандартом является MPI (message
passing interface -
интерфейс передачи сообщений) [1-3]. Конкретные реализации
MPI
стандарта создаются производителями программного обеспечения
и поставляются вместе с оборудованием. Большинство
реализаций стандарта
MPI
называются
MPICH.
Этот стандарт описывает имена, вызовы и результат работы
процедур. Для каждой конкретной параллельной системы с
передачей сообщений MPI имеет свою оптимизированную
реализацию, а правильно написанная программа переносима
между различными MPI системами на уровне исходных кодов. Для
написания MPI программ используются современные языки
программирования, такие как C/C++ и Fortran.
Исследования в области
MPI
программирования ведутся в двух направлениях: создание
эффективных параллельных алгоритмов и создание эффективных
реализаций
MPI
стандарта для кластерных систем. Параллельные алгоритмы
разрабатываются с учетом низкой скорости передачи данных, в
связи с этим предпочтение отдается методам с наименьшим
числом обменов. Текущая реализация
MPI
для кластерных систем осуществляет обмены посредством
протокола
TCP/IP
[4], что приводит к невозможности эффективного использования
широковещательных обменов, которые в текущей реализации
осуществляются посредством парных обменов. Поэтому сегодня
ведутся работы по созданию
MPI
реализации с реальным использованием широковещательных
пересылок. Еще одна возможность увеличения
производительности
MPI
программ – совмещение обменов и вычислений, однако для
используемой в работе реализации данная техника не приводит
к существенным улучшениям.
Данная работа посвящена созданию эффективных параллельных
алгоритмов метода сопряженных градиентов для симметрических
положительно определенных пятидиагональных систем линейных
алгебраических уравнений. Системы подобного рода появляются
при конечноразностной аппроксимации дифференциальных
уравнений в частных производных. На сегодняшний день
разработано большое число эффективных последовательных
алгоритмов данного типа [1]. Однако большинство из них
неприемлемо для параллельной реализации. Это связано с их
рекурсивным характером, а, следовательно, малым
параллелизмом.
Целью данной работы является исследование
существующих последовательных и параллельных алгоритмов
метода сопряженных градиентов, выделение из них, а также
создание собственных эффективных алгоритмов метода
сопряженных градиентов, пригодных для применения на
кластерных системах.
В
ходе работы было исследовано большое число алгоритмов метода
сопряженных градиентов. При выборе метода для исследования
предпочтение отдавалось методам с минимальным числом
межпроцессорных обменов. В результате этого было выделено
три класса методов: блочно-диагональные методы,
полиномиальные методы и методы аппроксимации обратной
матрицы.
Результаты исследования показали, что при реализации задачи
на кластерах больших размеров целесообразно использовать
методы с минимальным числом обменов, а на кластерах малых
размеров - методы, обладающие лучшей сходимостью.
1.
Вычислительный кластер
Кластер - это связанный
набор полноценных компьютеров, используемый в качестве
единого вычислительного ресурса [1,2].
В качестве
вычислительных узлов кластера используются доступные на
рынке одно-, двух- или четырехпроцессорные компьютеры.
Каждый узел такой системы работает под управлением своей
копии операционной системы, в качестве которой чаще всего
используются стандартные операционные системы: Windows,
Linux, Solaris и т.п. Состав и мощность узлов кластера может
меняться, давая возможность создавать неоднородные системы
[1,2].
В качестве
коммуникационного протокола в таких системах используются
стандартные протоколы ЛВС, характеризуемые низкой стоимостью
и низкой скоростью передачи данных. Основные характеристики
коммуникационных сетей: латентность – время начальной
задержки при посылке сообщения и пропускная способность сети,
определяющая скорость передачи информации по каналам связи
[1,2]. Наличие латентности определяет тот факт, что
максимальная скорость передачи данных по сети не может быть
достигнута на сообщениях с небольшой длиной. Чаще всего
используется сеть Fast Ethernet, основное достоинство
которой – низкая стоимость оборудования. Однако большие
накладные расходы на передачу сообщений в рамках Fast
Ethernet приводят к серьезным ограничениям на спектр задач,
которые можно эффективно решать на таком кластере. Если от
кластера требуется большая универсальность, то нужно
переходить на более производительные коммуникационные сети,
например, SCI, Myrinet и т.п.
В качестве средств
организации параллельного программирования в кластерах
используются различные системы передачи сообщений,
посредством которых осуществляется взаимодействие узлов
кластера. Наиболее распространенным на сегодняшний день
стандартом программирования для систем с передачей сообщений
является
MPI.
Конкретная
MPI
реализация создается производителями параллельных систем и
поставляется вместе с оборудованием.
Кластер кафедры ЭВМ, на котором
проводились исследования (рис 1.1)
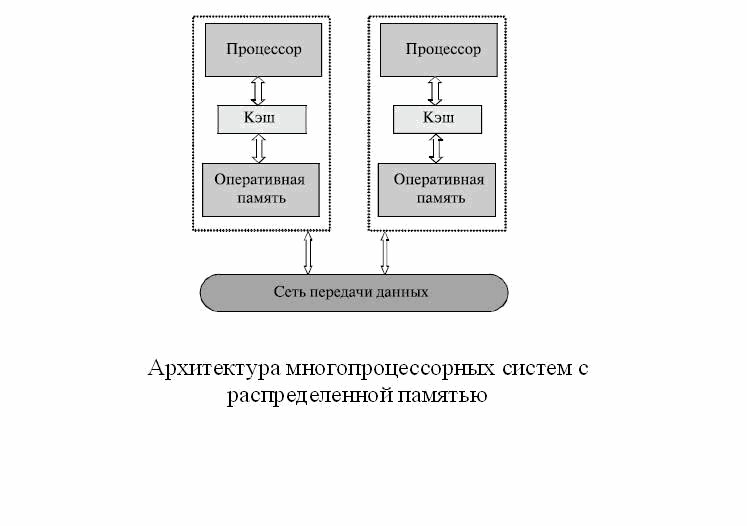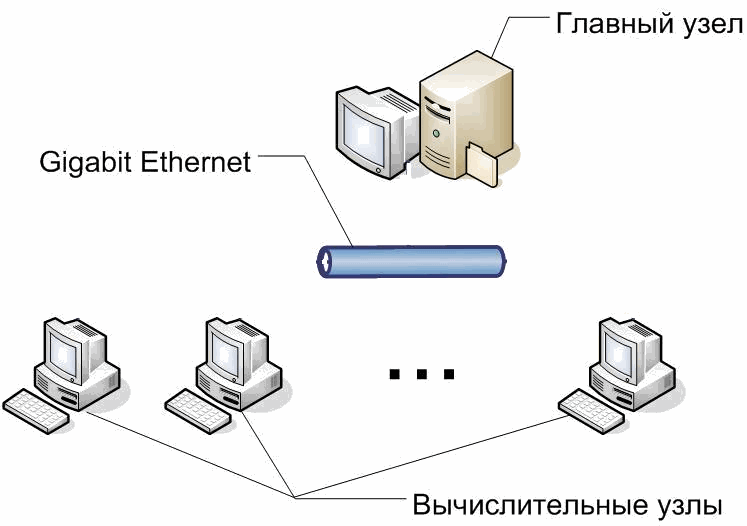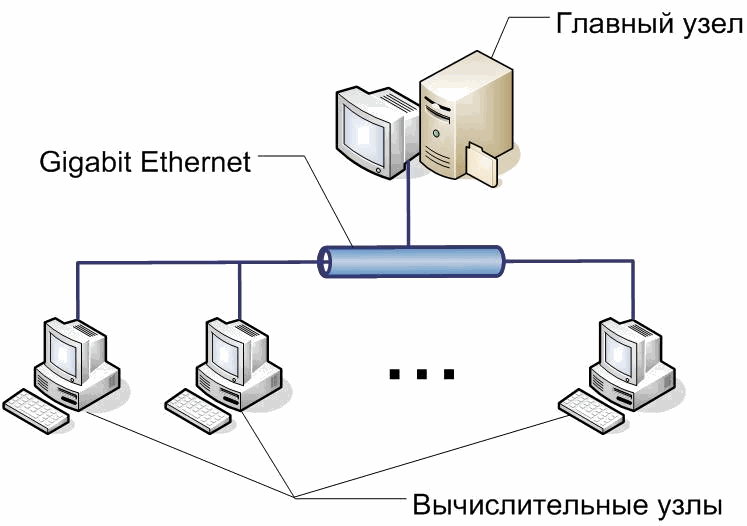
Рис1.
Структура кластера
Структура кластера
состоит из :
·
1
главный узел (head
node)
·
11
вычислительных узлов (compute
nodes)
·
cетевой
интерфейс
Gigabit
Ethernet,
1 Гбит/c
·
кластерное
ПО
– Microsot Windows Compute Cluster Server 2003
·
Языки
программирования – С, С++,
Fortran
·
Параллельное
программирование –
MPI
Технические характеристики кластера
Характеристики главного и вычислительных узлов
1.
Процессор:
Intel Pentium Core2 64bit, 1.86 ГГц
2.
Оперативная память: 1 Гб
3.
Жесткий диск: 80 Гб
4.
Сетевой интерфейс:
Gigabit
Ethernet,
1 Гбит/с
5.
Операционная
система:
Microsoft Windows Server
2003Enterprise
x64 Edition SP2
2.Интерфейс
передачи
данных
(message passing interface – MPI)
Для
организации информационного взаимодействия между
процессорами в самом минимальном варианте достаточно
операций приема и передачи данных (при этом, конечно, должна
существовать техническая возможность коммуникации между
процессорами – каналы или линии связи). В MPI существует
целое множество операций передачи данных. Они обеспечивают
разные способы пересылки данных. Именно данные возможности
являются наиболее сильной стороной MPI (об этом, в частности,
свидетельствует и само название MPI).
Подобный
способ организации параллельных вычислений получил
наименование модели "одна программа множество процессов"
(single program multiple processes or SPMP1)).
разработкой параллельных программ с применением MPI
[2-4].
·
MPI позволяет в значительной степени снизить остроту
проблемы переносимости параллельных программ между разными
компьютерными системами – параллельная программа,
разработанная на алгоритмическом языке C или FORTRAN с
использованием библиотеки MPI, как правило, будет работать
на разных вычислительных платформах;
·
MPI содействует повышению эффективности параллельных
вычислений, поскольку в настоящее время практически для
каждого типа вычислительных систем существуют реализации
библиотек MPI, в максимальной степени учитывающие
возможности компьютерного оборудования;
·
MPI уменьшает, в определенном плане, сложность
разработки параллельных программ, т. к., с одной стороны, а
с другой стороны, уже имеется большое количество библиотек
параллельных методов, созданных с использованием MPI.
3.Классификация параллельных методов решения СЛАУ
Метод Гаусса–Зейделя.
Пусть решаемая система представлена в виде[1-2]
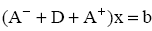
Итерационная схема Гаусса–Зейделя следует из этого
представления системы:
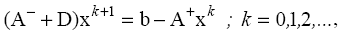
или
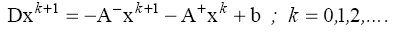
Приведем метод Гаусса–Зейделя к стандартному виду:
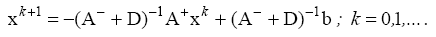
Стандартная форма метода позволяет выписать его
итерационную матрицу и провести над ней очевидные
преобразования:
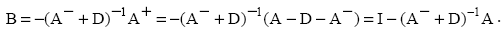
Представим метод Гаусса–Зейделя в координатной форме для
системы общего вида:
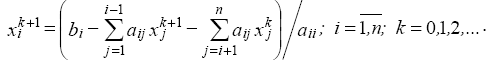
Координатная форма метода Гаусса–Зейделя отличается от
координатной формы метода Якоби лишь тем, что первая
сумма в правой части итерационной формулы содержит
компоненты вектора решения не на k-й, а на (k+1)-й
итерации.
Параллельный алгоритм метода Гаусса–Зейделя
Отличие
метода Гаусса–Зейделя от метода простой итерации
заключается в том, что новые значения вектора
вычисляются не только на основании значений предыдущей
итерации, но и с использованием значений уже вычисленных
на данной итерации .
Текст
последовательной программы для вычисления новых значений
компонент вектора представлен ниже.
void
GaussZeidel (double *A, double *X, int size)
/* задана матрица А,
начальное приближение вектора Х,
размерность матрицы
size, вычисляем новое значение вектора Х */
{ unsigned
int i, j;
double Sum;
for (i = 0;
i < size; ++i) {
Sum = 0;
for (j = 0;
j < i; ++j)
Sum +=
A[ind(i,j,size)] * X[j];
for (j =
i+1; j < size; ++j)
Sum +=
A[ind(i,j,size)] * X[j];
X[i]=(A[ind(i,size,size)]
– Sum) / A[ind(i,i,size)];
}
}
Рис. 2. Процедура
вычисления значений вектора по методу Гаусса-Зейделя
Следующая система
уравнений описывает метод Гаусса-Зейделя.
Вычисления каждой
координаты вектора зависят от значений, вычисленных на
предыдущей итерации, и значений координат вектора
вычисленных на данной итерации. Поэтому нельзя
реализовывать параллельный алгоритм, аналогичный методу
простой итерации: каждый процесс не может начинать
вычисления пока, не закончит вычисления предыдущий
процесс.
Можно предложить
следующий модифицированный метод Гаусса–Зейделя для
параллельной реализации. Разделим вычисления координат
вектора по процессам аналогично методу простой итерации.
Будем в каждом процессе вычислять свое количество
координат вектора по методу Гаусса Зейделя, используя
только вычисленные значения вектора данного процесса.
Различие в параллельной реализации по сравнению с
методом простой итерации заключается только в процедуре
вычисления значений вектора (вместо процедуры
Iter_Jacoby используем процедуру
Gauss-Seidel).
void
GaussZeidel(int size, int MATR_SIZE, int first)
/* задана матрица А,
размерность матрицы MATR_SIZE, количество
вычисляемых элементов
вектора в данном процессе size, вычисляем новые
значения вектора Х с
номера first, используя значения вектора Х */
{ int i, j;
double Sum;
for (i = 0;
i < size; ++i) {
Sum = 0;
for (j = 0;
j < i+first; ++j)
Sum +=
A[ind(i,j,MATR_SIZE)] * X[j];
for (j =
i+1+first; j < MATR_SIZE; ++j)
Sum +=
A[ind(i,j,MATR_SIZE)] * X[j];
X[i+first]=(A[ind(i,MATR_SIZE,MATR_SIZE)]
– Sum) /
A[ind(i,i+first, MATR_SIZE)];
}
}
Рис. 1. Процедура вычисления значений вектора по
методу Гаусса–Зейделя(параллельная версия)
4.Направления дальнейших исследований
-
•Разработка
программной системы для
параллельного решения СЛАУ на
кластере
-
•Сравнение
эффективности различных
параллельных методов решения
СЛАУ на кластере
Литература
1. Программирование
для многопроцессорных систем в стандарте MPI:
Пособие / Г. И.
Шпаковский,
Н. В. Серикова. – Мн.: БГУ, 2002. – 323с.
2.
Теория и практика параллельных
вычислений: учебное пособие/ В.П.Гергель.- М.:
Интернет- Университет Информационных технологий;
Бином. Лаборатория знаний, 2007.-423с.
3.
Компьютерные сети. Принципы, технологии,
протоколы / В. Г. Олифер, Н. А. Олифер. – СПб: Питер, 2001.
– 672с.
4. Параллельное программирование
с использованием Open MP.-М.: Бином. Лаборатория знаний
Интуит., 2008.- 118с.
5.
Group W, Lusk E,
Skjellum A. Using MPI. Portable Parallel Programming with
the Message-Passing Interface. - MIT Press, 1994. (http://www.mcs.anl.gov/mpi/index.html)
6. Параллельные информационные технологии: учебное
пособие/ А.Б. Барский-
M.:
Интернет- Университет Информационных технологий; Бином.
Лаборатория знаний, 2007.-504с.
7.
Корнеев В.Д.
Параллельное программирование в MPI. - Москва-Ижевск:
Институт компьютерных исследований, 2003. - 304 с.
8.
Миллер Р., Боксер Л. Последовательные и параллельные
алгоритмы: Общий подход. - М.: БИНОМ. Лаборатория знаний,
2006. - 406 с.
9. посвященный международной
конференции по высокопроизводительным вычислениям
(http://www.supercomp.de)
10.
Антонов А.С. Параллельное программирование с использованием
технологии MPI: Учебное пособие
(http://parallel.ru/tech/tech_dev/MPI/)
|