Щеглов Максим Игоревич
Факультет: Вычислительной техники и информатики
Специальность: Программное обеспечение автоматизированных систем
Тема магистерской диссертации: "Анализ и оценка эффективности параллельных многошаговых блочных методов решения ОДУ на кластере"
Научный руководитель: Фельдман Лев Петрович профессор, д.т.н.
Библиотека
Авторы: Л.П. Фельдман, И.А. Назарова
Донецкий национальный технический университет
Украина, 83001, Донецк, ул. Артема, 66.
Применение технологии локальной экстраполяции для высокоточного решения задачи Коши на SIMD-структурах
Abstract
Feldman L.P., Nazarova I.A. Application of the local extrapolation technology for high exact solution of Cauchy’s problem on the SIMD-structures. Parallel algorithms for system’s of ordinary differential equations on base the method of local extrapolation provided high exact solutions are considerated. The potential system and algorithm parallelism is exploited. Obtained algorithms are realized on SIMD-structures with matrix topology. The estimations of the execution time, acceleration and efficiency parallel solution are defined.
Введение
В различных предметных областях часто встречаются в качестве математических моделей изучаемых процессов системы обыкновенных дифференциальных уравнений(СОДУ) большой размерности. Бурное развитие большинства современных естественно-научных направлений поставило проблему создания новых, высокоточных (10-15 – 10-20) методов численного интегрирования таких систем. Традиционный подход к решению этой проблемы, а именно применение явных методов Рунге-Кутты высоких порядков является неэффективным из-за многократного вычисления правых частей дифференциальных уравнений[1,2]. Методы численного интегрирования, использующие "старшие" производные, также вызывают трудности, поскольку в реальных задачах не всегда можно вычислить производные аналитически. Интересным и плодотворным является подход, базирующийся на идее локальной экстраполяции Ричардсона, привлекательность которого резко возросла в связи с развитием высокопроизводительных параллельных вычислительных систем.
1.Общая характеристика технологии локальной экстраполяции
Пусть численно решается задача Коши для системы обыкновенных дифференциальных уравнений с известными начальными условиями:
.
(1)
Интегрирование такой системы с некоторой наперед заданной точностью возможно при существовании механизма управления шагом интегрирования на основе определения апостериорной локальной погрешности. Известными способами решения этой проблемы являются: дублирование шага по правилу Рунге, вложенные методы Рунге-Кутты[1,2]. Метод локальной экстраполяции Ричардсона является обобщением технологии удвоения шага по правилу Рунге. Идея этого метода заключается в многократном измельчении шага интегрирования, и также в многократном применении процесса вычисления, названного локальной экстраполяцией (см. рис. 1) .
Рисунок 1 – Технология локальной экстраполяции
Решение задачи Коши рассматривается при переходе из точки
в точку
,
- базовая длина шага,
. Выбирается ряд натуральных чисел такой, что:
и, соответственно, последовательность шагов:
, где
. Задается опорный численный метод порядка
и, выполняя
шагов интегрирования длиной
, вычисляют приближенное решение исходной задачи:
.
(2)
Выполнив вычисления для ряда последовательных значений i, по реккурентному соотношению(2) определяют экстраполированные значения
для произвольных i,j по формуле (3)[]. Этот процесс получил название локальная полиномиальная экстраполяция:
.
(3)
Здесь величина b равна
единице в общем случае, в тоже время для симметричных опорных
методов, имеющих разложение погрешности по степеням 
, b равно двум (каждая экстраполяция исключает две степени h
вместо одной)[2-3]. Достоинство этого метода состоит в том, что он дает
полную таблицу результатов вычислений, которые образуют
последовательность вложенных методов и позволяют оценить
локальную погрешность, выбрать стратегию для методов переменного
порядка.
Таблица 1 – Экстраполяционная таблица
| p | p+b | p+2b |
p
|
|
|
|
|||||
|
|
||||
|
|
|
|||
| … | ……… | ... | … |
|
|
|
|
|
… |
|
|
В таблице (1)
- есть приближенное решение задачи Коши, полученное численным методом порядка
с шагом
. Величина
соответствует аппроксимации наивысшего порядка, равного 2k, в случае, если вычислены первые k строк экстраполяционной таблицы, а величина
соответствует аппроксимации порядка 2k-2. Для управления шагом интегрирования естественно использовать выражение:
.
Экстраполяционные методы имеют то преимущество, что у них на каждом шаге можно менять не только длину шага, но и порядок метода. Следовательно, экстраполяцию можно рассматривать как метод с переменным порядком (столбцы таблицы) и переменным шагом интегрирования (строки таблицы).
Для получения множества шагов интегрирования используются числовые последовательности, образованные гармоническим рядом, степенями двойки, различными четными рядами чисел.
Таким образом, экстраполяционная технология Ричардсона включает численный метод решения задачи Коши, последовательность сеток, рекуррентное правило вычисления значений приближенного решения. Эффективность применения технологии локальной экстраполяции напрямую зависит от правильного выбора и сочетания всех трех составляющих этого метода.
2. Исследование эффективности последовательных алгоритмов на основе метода локальной экстраполяции
Наиболее эффективным последовательным методом, реализующим технологию локальной полиномиальной экстраполяции cчитается алгоритм Грэгга-Булирша-Штера(ГБШ), базирующийся на модифицированном методе средней точки [3]:
(4)
Оценим
вычислительную сложность этого метода, используя тот факт, что опорный
метод ГБШ имеет второй порядок точности и допускает разложение по
степеням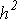 
. Накладные расходы для получения решения экстраполяционным методом порядка
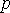на основе (4) определяются количеством обращений к функции f – правой части уравнения (1):
.
Несколько числовых рядов положительных чисел применяются для обеспечения последовательности сеток интегрирования[1:
1)
= 2,4,8,16,32,64,128,… –
;
2)
= 2,4,6,8,10,12,14,16,20,22,… –
;
(5)
3)
= 2,4,6,8,12,16,24,32,48,64,… –
.
Эффективность использования той или иной, обязательно четной, последовательности натуральных чисел для расчета шагов интегрирования в методе ГБШ можно оценить по графикам рисунка 2:
Рис.2 – Эффективность использования четных последовательностей
На рисунке 2 представлены зависимости объемов вычислительной работы
от порядка
экстраполяционного метода. Наиболее оптимальной
последовательностью является вторая четная последовательность с
минимальным числом вычислений f, для которой: 
.
Рассмотрим применение рассмотренной выше технологии для решения систем линейных однородных уравнений с постоянными коэффициентами :
(6)
Для сравнения возьмем оптимальный метод ГБШ и оригинальный экстраполяционный экспоненциальный алгоритм на основе гармонического ряда. Точным решением задачи Коши вида (6) является матричная експонента:
,
.
Приближенное решение (6) можно построить, аппроксимировав матричную экспоненту отрезком ряда Тейлора :
,
(7)
причем, (7) определяет численный метод решения (6) порядка
[1].
Время последовательной реализации метода ГБШ без учета локальной экстраполяции:
где
– время умножения матрицы на вектор;
– время умножения вектора на скаляр;
– время выполнения сложения векторов.
Время последовательной реализации экстраполяционного экспоненциального метода без локальной экстраполяции:
,
где
– время вычисления скалярного произведения матриц;
- время сложения двух матриц,
– время умножения матрицы на скаляр. Заметим, что для получения метода порядка p в случае ГБШ и любого другого симметричного метода необходимо вычислить
строк экстраполяционной таблицы, а для экспоненциального метода – р-1- строку.
График зависимости времени обоих последовательных алгоритмов
с учетом локальной экстраполяции от порядка метода p и размерности исходной системы линейных дифференциальных уравнений m
приведен на рисунках 3 и 4(здесь и далее пунктирная линия соответствует
экспоненциальному методу, а сплошная – методу ГБШ).
Рисунок 3а - Графики времени выполнения последовательных алгоритмов ГБШ и экспоненциального от размерности системы
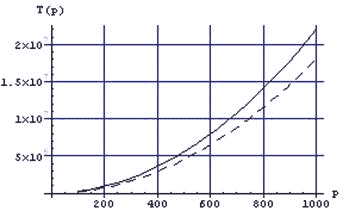
Рисунок 3б - Графики времени выполнения последовательных алгоритмов ГБШ и экспоненциального от порядка метода
Таким образом, экстраполяционный экспоненциальный метод решения СЛОДУ с постоянными коэффициентами даже без наличия
- экстраполяции требует существенно меньшего времени для последовательной реализации.
3. Оценка качества параллельных алгоритмов с локальной экстраполяцией
Рассмотрим
отображение описанных алгоритмических схем с локальной
экстраполяцией на многопроцессорные вычислительные
системы SIMD-структуры с распределенной памятью. Конфигурацию
системы считаем фиксированной: число процессорных элементов
и схема их соединения не изменяются в процессе счета. Каждый процессор
может выполнить любую арифметическую операцию за один такт, временные
затраты, связанные с обращением к памяти отсутствуют. Параллельная
реализация рассмотренных методов в применении к СЛОДУ требует
распараллеливания таких базовых операций, как матричное и
векторное умножение и сложение, поэтому в качестве топологического
решения принимается замкнутая решетка 
или тор. На такой топологической схеме наиболее
эффективно выполняются матричные операции. Для простоты изложения
рассмотрим случай, когда количество процессорных элементов в
строке или столбце матрицы совпадает с размерностью задачи, m.
Вычисление матричного умножения и умножения матрицы на вектор
может быть выполнено по систолическому алгоритму, который
является наиболее эффективным для SIMD- систем[5]:
,
(8)
где
,
,
- времена выполнения одиночных операций умножения, сложения и
сдвига. Вычисление систолического умножения матрицы на
вектор на базе алгоритма сдваивания, подробно описано в [6] и
требует следующего времени выполнения:
(9)
и
.
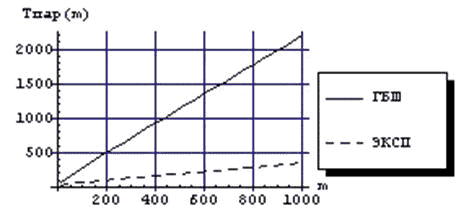
Рисунок 4 – Зависимость времени выполнения параллельных алгоритмов от размерности системы
В качестве показателей эффективности параллельных алгоритмов будем использовать коэффициенты ускорения и эффективности.
Коэффициент ускорения, получаемого при использовании параллельного алгоритма для p процессоров, по сравнению с последовательным вариантом выполнения вычислений определяется:
,
как отношение времени решения на однопроцессорной ЭВМ:
к времени выполнения параллельного алгоритма:
. Величина
- параметр, количество входных данных задачи, в данном конкретном случае порядок СОДУ. Величина
может быть определена, как минимально возможное время выполнения
параллельного алгоритма при использовании неограниченного числа
процессоров (концепция паракомпьютера):
.
Эффективность использования параллельным алгоритмом процессоров при решении задачи определяется :
.
Величина эффективности определяет среднюю долю времени выполнения алгоритма, в течении которой процессоры реально используются для решения задачи. Графики зависимости характеристик параллелизма от размерности исходной задачи приведены на рисунках 6 и 7.
При расчете характеристик эффективности считаем, что последовательные варианты этих схем реализованы на однопроцессорной ВС с быстродействием арифметического процессора и объемом ОЗУ равным суммарному объему всех ЗУ арифметических процессоров и с необходимым числом внешних устройств, имеющих скорости обмена такие же, что и МПВС типа SIMD.
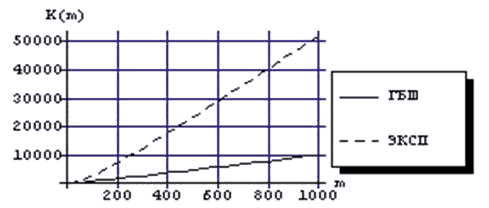
Рис. 6 – Зависимость коэффициентов ускорения от порядка системы
Рис. 7 – Зависимость коэффициентов эффективности от порядка системы
Таким образом, предложенный экспоненциальный метод со схемой локальной экстраполяции имеет высокие характеристики потенциального и реального параллелизма при решении СЛОДУ.
Определение характеристик параллелизма осуществлялось с помощью пакета MathematicaÒ (Wolfram Research Inc.).
Заключение
Численный эксперимент и проведенный сравнительный анализ различных последовательных и параллельных вычислительных схем на основе технологии локальной экстраполяции показал как достоинства этого подхода, так и его недостатки. Основным недостатком этого подхода является его высокая вычислительная сложность при решении задач общего вида, даже для наиболее эффективных из известных последовательных методов, таких как ГБШ. Областью приложения экстраполяционных методов остаются высокоточные применения, где такие накладные расходы могут быть оправданными. Одним из путей решения этой проблемы является разработка новых узкоспециализированных методов в рамках общей технологии экстраполяции, а также построение параллельных алгоритмов и схем их отображения на структуры многопроцессорных ВС.
Перспективным направлением дальнейших исследований является
оценка области и характера устойчивости полученных методов, анализ влияния различных топологий соединения процессоров на характеристики качества параллельных алгоритмов, разработка параллельных алгоритмов для решения СОДУ общего вида.
Литература
- Хайрер Э., Нёрсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи: Пер. с англ. – М.: Мир, 1990. – 512с.
- Арушанян О.Б., Залеткин С.Ф. Численное решение обыкновенных дифференциальных уравнений на Фортране.– М.: МГУ,1990.–336с.
- Houwen P.J., Sommeijer B.P. Parallel ODE solver.// Proceedings of the International Conference on Supercomputing. –ACM Press, 1990,p.71-81.
- Jackson K.R., Norsett S.P. The potential for parallelism in Runge-Kutta methods. Part 1: R-K formulas in standard form, SIAM J.Numer. Anal. 32,p.49-82.
- Бройнль Т. Паралельне програмування: Початковий курс: Навч. посібник/ Вступ.слово А.Ройтера;Пер. з нім. В.А.Святного. – К.: Вища шк.,1997. –358с.