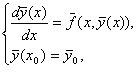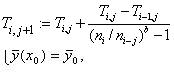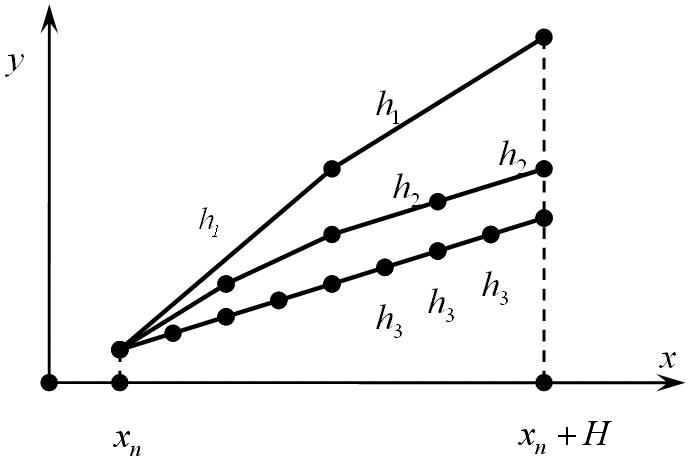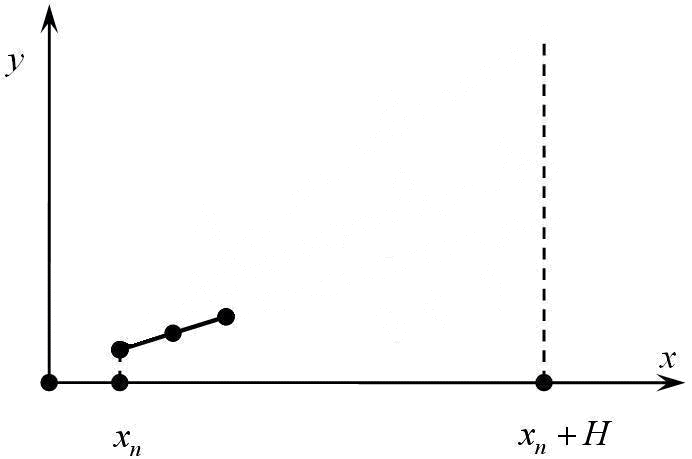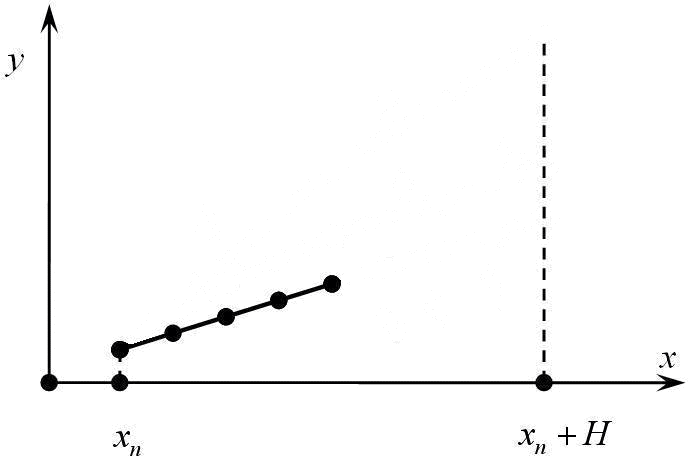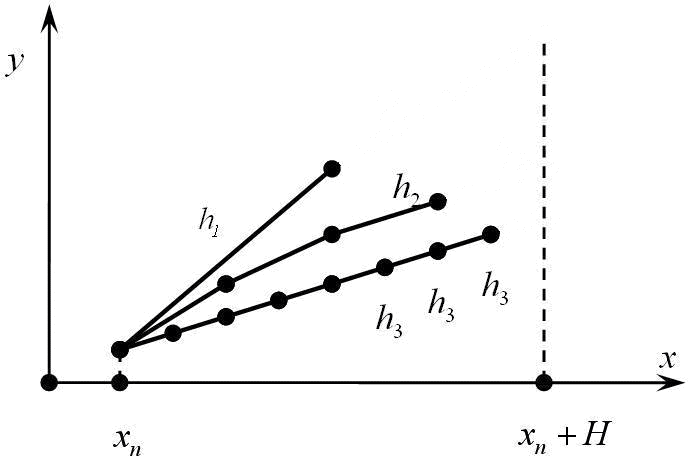
Автореферат з теми випускної роботи магістра

Введення

Системи звичайних диференційних рівнянь (СЗДР) великої розмірності є найважливішим інструментом для опису безлічі явищ та процесів різної природи. Висока обчислювальна складність чисельного рішення багатовимірних початкових завдань вимагає побудови ефективних паралельних алгоритмів для інтегрування таких систем. Сучасний ефективний алгоритм чисельного розв'язання задачі Коші для СЗДР повинен містити механізм управління кроком інтегрування на основі інформації про локальну апостеріорної похибки. Одним з відомих способів оцінки крокової похибки є технологія локальної екстраполяції, що володіє високим ступенем внутрішнього паралелізму, а, отже, перевагами при реалізації на паралельних комп'ютерах. Метою даної роботи є розробка і аналіз ефективності паралельних екстраполяціонних однокрокових методів, а також програмну реалізацію розроблених програм.

Актуальність

Диференціальні рівняння та системи диференціальних рівнянь є найважливішим інструментом для опису безлічі явищ і процесів, що відбуваються в світі (фізичні, біологічні, хімічні і т.д.) Результати досліджень часто являють собою системи диференціальних рівнянь великих розмірів, що робить їх рішення дуже трудомістким на однопроцесорних системах. Мультипроцесорні ж системи набагато полегшують цей процес, що робить рішення задачі Коші і подальші розробки в даній області актуальними на сьогоднішній день.

Наукова новизна

Запропоновані паралельні алгоритми чисельного рішення нелінійної задачі Коші для СЗДР на базі явних і неявних однокрокових схем з вбудованими способами оцінки локальної апостеріорної похибки: локальна екстраполяція Річардсона.

Мета і завдання розробки та дослідження

Мета роботи

Aналіз й рішення завдання Коші екстраполяціонним однокрокових паралельним методом з використанням різних видів топологій, а також характеристик розпаралелювання на обчислювальному кластері, розробка і реалізація програмної системи, що дозволяє отримати рішення даної задачі.

Завдання

Вивчення багатокрокових паралельних блокових методів рішення задачі Коші, рішення задачі Коші даними методами на обчислювальному кластері з використанням Microsoft Visual Studio 2005 і технології Message Passing Interface (MPI).

Рішення завдання і результати досліджень

Метод локальної екстраполяції Річардсона (ЛЕР) є узагальненням технології подвоєння кроку за правилом Рунге [1-2]. Ідея методу полягає в багаторазовому подрібненні кроку інтегрування, і також в багаторазовому застосуванні процесу обчислення - локальна екстраполяція (Мал. 1).

Мал.1. Технологія локальної екстраполяції (анімація: об'єм - 49,7 КБ, кількість кадрів - 9, кількість циклів повторення - 5, розмір - 692x459)

Рішення задачі Коші для систем звичайних диференціальних рівнянь першого порядку

розглядається при переході з точки в точку , де H – базова довжина кроку. Обирається ряд натуральних чисел такий, що: і, відповідно, послідовність кроків інтегрування: , де . Задається опорний чисельний метод порядку і, обчислюється наближене рішення вихідної задачі: . Виконавши обчислення для ряду послідовних значень i, по рекурентного співвідношення (2), визначають – екстрапольовані значення для довільних i, j (Мал. 2). Процес обчислення за (2) отримав назву Поліноміальна екстраполяція Ейткен-Невілла [1-3]:

Тут величина b дорівнює одиниці у загальному випадку, в теж час для симетричних опорних методів b дорівнює двом.

Мал.2 Обчислення за схемою поліноміальної екстраполяції, при k=4

Екстраполяціонная технологія включає:

1. опорний чисельний метод розв'язання задачі Коші
2. послідовність сіток
3. рекурентної правило обчислення значень наближеного рішення

Ефективність застосування ЛЕР безпосередньо залежить від правильного вибору і поєднання всіх трьох складових. В якості опорного методу був обраний метод Рунге-Кутта 4-го порядку. Даний метод є симетричним. Це означає, що він має асимптотичну розкладання за ступенями, і кожна екстраполяція виключає два ступені. Тоді, кількість рядків екстраполяціонной таблиці, визначається з наступного співвідношення:

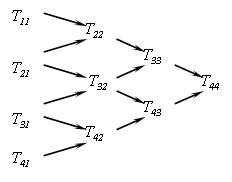
Мал.3 Екстраполяційна таблиця

Отже, якщо обчислені k рядків екстраполяціонной таблиці, то для симетричних опорних методів маємо в якості апроксимації найвищого порядку точності, рівного 2k, при цьому точність апроксимації складе - (2k - 2). Для отримання множини кроків інтегрування використовується числова послідовність: , що дозволяє скористатися властивістю симетричності [3].

Гідність цього методу полягає в тому, що він дає повну таблицю результатів обчислень, які утворюють послідовність вкладених методів, і дозволяють оцінити локальну похибка, вибрати стратегію для методів змінного порядку. У таблиці (1) – є наближений розв'язок задачі Коші, отримане чисельним методом порядку з кроком

Екстраполяціонние методи мають ту перевагу, що у них на кожному кроці можна міняти не тільки довжину кроку, але й порядок методу. Отже, екстраполяцію можна розглядати як метод зі змінним порядком (стовпці таблиці) і змінним кроком інтегрування (рядки таблиці).

Потенційно обчислення за технологією локальної екстраполяції містять три джерела внутрішнього паралелізму:

• системний паралелізм (обмежений розмірністю СЗДР).
• паралелізм екстраполяції (обмежений розмірністю таблиці екстраполяції).
• паралелізм опорного методу (мала ступінь паралелізму).

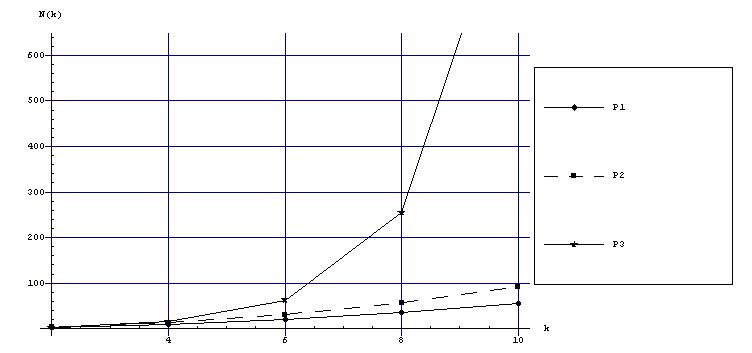
Оскільки в основу обчислень покладена явна чисельна схема, реально є можливість використовувати системний і екстраполяціонний паралелізм.

Для отримання множини кроків інтегрування розглянемо числові послідовності, утворені гармонійним поруч, ступенями двійки, парними рядами чисел [Х]:

Ефективність використання послідовностей натуральних чисел для розрахунку кроків інтегрування в методі локальної екстраполяції можна оцінити за графіками рисунка 3, де показана залежність накладних витрат на формування сіток інтегрування від довжини екстраполяціонной таблиці. При одному і тому ж опорному методі найбільш витратною є послідовність , яка фактично повторює процес подвоєння кроку, а найбільш ефективними є послідовності і . Вибір опорного методу інтегрування базується на дослідженні впливу порядку методу і його властивостей на обсяг необхідних обчислень. Нехай опорний метод має порядок – , довжина екстраполяціонной таблиці дорівнює k, а число стадій явного методу - s, визначимо необхідний розмір екстраполяціонной таблиці для отримання рішення методом порядку r.

Мал.4 Накладні витрати при використанні чисельних послідовностей від числа рядків екстраполяційної таблиці для довільного опорного методу

Підсумовуючи всі отримані результати, можна зробити висновок, що для зменшення накладних витрат при застосуванні технології локальної екстраполяції, слід вибирати опорний метод малого порядку, зокрема другого, але з достатніми властивостями стійкості. Однак, є ще один момент вимагає аналізу. Теоретично немає ніяких обмежень на довжину екстраполяціонной таблиці, але кінцівку пам'яті машини і накопичення помилок округлення, обмежують довжину екстраполяціонной таблиці зверху і, як правило, використовується . Тому, для отримання високоточної рішення не є іншої можливості отримати рішення, як використовувати технологію Річардсона на базі опорного методу високого порядку.

Загальна схема алгоритму локальної екстраполяції:

1. визначається розмірність екстраполяціонной таблиці на основі необхідного порядку екстраполяціонного методу;
2. відповідно до використовуваним типом паралелізму розподіляються дані між процесорами;
3. обчислюється початкове наближення, на основі опорного методу (перший стовпець екстраполяціонной таблиці);
4. обчислюються значення екстраполяціонной таблиці за формулою Ейткен-Невілла;
5. виконуються необхідні пересилання даних між процесорами через керуючий процесор у силу особливостей вибраної топології.

Висновки

Порівняльний аналіз динамічних характеристик паралельних алгоритмів локальної екстраполяції на основі явних методів Рунге-Кутта показав, що областю додатків ЛЕР є високоточне рішення, складна права частина та багатовимірні завдання, однак потрібен ретельний облік всіх складових паралельної системи для того, щоб таке рішення було ефективним. Планується провести дослідження з використанням різних топологій, варіюванням числових послідовностей для генерації сіток інтегрування, а також застосуванням неявних опорних методів, придатних для вирішення жорстких задач. Отримані результати будуть використані при розробці бібліотеки паралельного чисельного аналізу для кластера WCCS-2003 Донецького національного технічного університету.

Література

1. Хайрер Э., Нерсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи.– М.: Мир, 1990. – 512с.
2. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи: Пер. с англ. – М.: Мир, 1999. – 685с.
3. Холл Дж.,Уатт Дж. Современные численные методы решения обыкновенных дифференциальных уравнений. – М.: Мир, 1999. – 311с.
4. Вержбицкий В.М. Основы численных методов. – М.: Высшая школа, 2002. – 840с.
5. Арушанян О.Б., Залеткин С.Ф. Численное решение обыкновенных дифференциальных уравнений на Фортране.– М.: МГУ,1990.–336с.
6. Foster I. Designing and Building Parallel Programs. – Addison-Wesley, 1999. – 302 с.
7. Немнюгин С.А., Стесик О.Л. Параллельное программирование для многопроцессорных ВС. – СПб.: БХВ-Петербург, 2002. – 400 с.
8. Гергель В.П., Стронгин Р.Г. Основы параллельных вычислений для многопроцессорных вычислительных машин. – Нижний Новгород: Изд-во ННГУ им. Н.И.Лобачевского, 2000. – 176с.
9. Арушунян О.Б., Залеткин С.Ф., Калиткин Н.Н. Тесты для вычислительного практикума по обыкновенным дифференциальным уравнениям.// Вычислительные методы и программирование, 2002, т.3, c.11-19.
10. Thomas Rauber, Gudula Runger Lecture Notes in Computer Science 817 [Електронний ресурс]: http://citeseerx.ist.psu.edu/viewdoc/download&rep=rep1&type=pdf