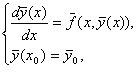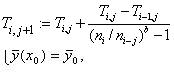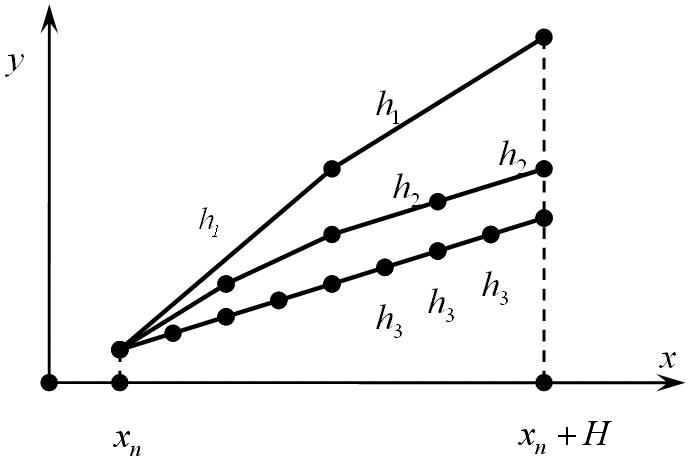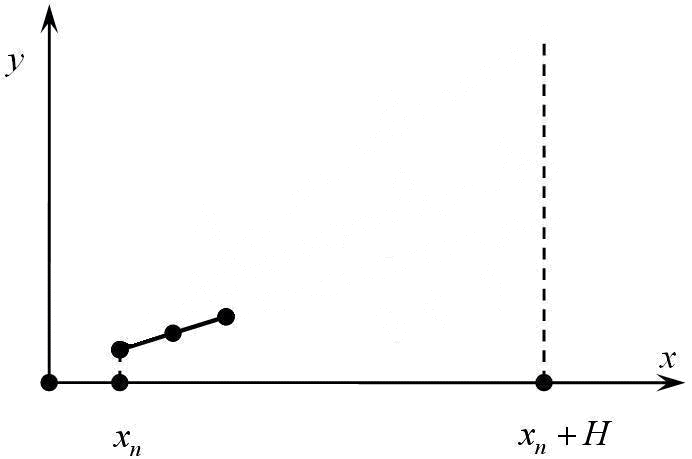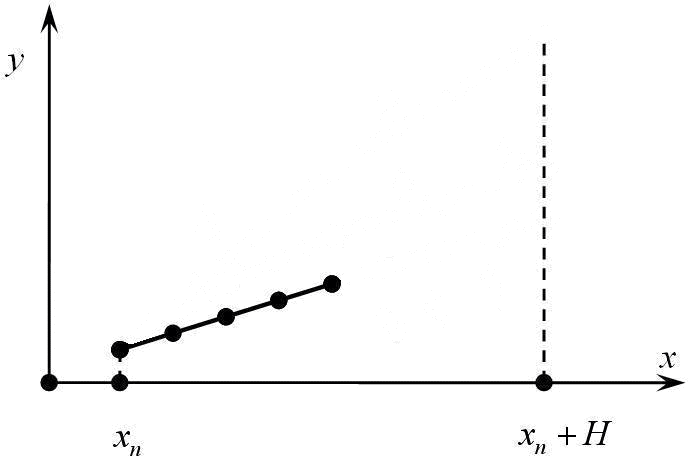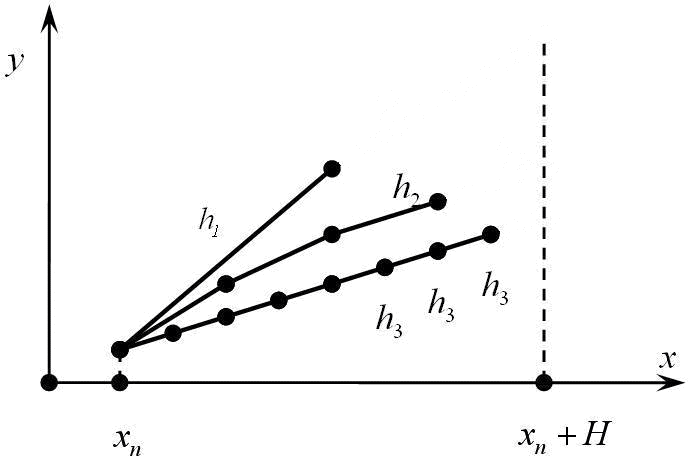
Автореферат по теме выпускной работы магистра

Введение

Системы обыкновенных дифференциальных уравнений (СОДУ) большой размерности являются важнейшим инструментом для описания множества явлений и процессов различной природы. Высокая вычислительная сложность численного решения многомерных начальных задач требует построения эффективных параллельных алгоритмов для интегрирования таких систем Современный эффективный алгоритм численного решения задачи Коши для СОДУ должен содержать механизм управления шагом интегрирования на основе информации о локальной апостериорной погрешности. Одним из известных способов оценки шаговой погрешности является технология локальной экстраполяции, обладающая высокой степенью внутреннего параллелизма, а, следовательно, преимуществами при реализации на параллельных компьютерах. Целью данной работы является разработка и анализ эффективности параллельных экстраполяционных одношаговых методов, а также программная реализация разработанных приложений.

Актуальность

Дифференциальные уравнения и системы дифференциальных уравнений являются важнейшим инструментом для описания множества явлений и процессов, происходящих в мире (физические, биологические, химические и т.д.) Результаты исследований часто представляют собой системы дифференциальных уравнений больших размеров, что делает их решение очень трудоемким на однопроцессорных системах. Мультипроцессорные же системы намного облегчают этот процесс, что делает решение задачи Коши и дальнейшие разработки в данной области актуальными на сегодняшний день.

Научная новизна

Предложены параллельные алгоритмы численного решения нелинейной задачи Коши для СОДУ на базе явных и неявных одношаговых схем с встроенными способами оценки локальной апостериорной погрешности: локальная экстраполяция Ричардсона.

Цель и задачи разработки и исследования

Цель работы

Aнализ и решение задачи Коши экстраполяционным одношаговым параллельным методом с использованием различных видов топологий, а также характеристик распараллеливания на вычислительном кластере, разработка и реализация программной системы, позволяющей получить решение данной задачи.

Задачи

Изучение многошаговых параллельных блочных методов решения задачи Коши, решение задачи Коши данными методами на вычислительном кластере с использованием Microsoft Visual Studio 2005 и технологии Message Passing Interface (MPI).

Решение задачи и результаты исследований

Метод локальной экстраполяции Ричардсона (ЛЭР) является обобщением технологии удвоения шага по правилу Рунге [1-2]. Идея метода заключается в многократном измельчении шага интегрирования, и также в многократном применении процесса вычисления – локальная экстраполяция (рис. 1).

Рис.1. Технология локальной экстраполяции (анимация: объем — 49,7 КБ, количество кадров — 9, количество циклов повторения — 5, размер — 692x459)

Решение задачи Коши для систем обыкновенных дифференциальных уравнений первого порядка

рассматривается при переходе из точки в точку , где H – базовая длина шага. Выбирается ряд натуральных чисел такой, что: и, соответственно, последовательность шагов интегрирования: , где . Задается опорный численный метод порядка и, вычисляется приближенное решение исходной задачи: . Выполнив вычисления для ряда последовательных значений i, по рекуррентному соотношению (2), определяют – экстраполированные значения для произвольных i, j (рис. 2). Процесс вычисления по (2) получил название полиномиальная экстраполяция Эйткена-Невилла [1-3]:

Здесь величина b равна единице в общем случае, в тоже время для симметричных опорных методов b равно двум.

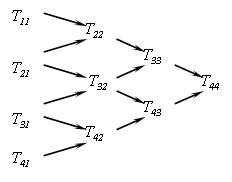
Рис.2 Вычисления по схеме полиномиальной экстраполяции, при k=4

Экстраполяционная технология включает:

1. опорный численный метод решения задачи Коши
2. последовательность сеток
3. рекуррентное правило вычисления значений приближенного решения

Эффективность применения ЛЭР напрямую зависит от правильного выбора и сочетания всех трех составляющих. В качестве опорного метода был выбран метод Рунге-Кутта 4-го порядка. Данный метод является симметричным. Это значит, что он имеет асимптотическое разложение по степеням , и каждая экстраполяция исключает две степени. Тогда, количество строк экстраполяционной таблицы, определяется из следующего соотношения:

Рис.3 Экстраполяционная таблица

Следовательно, если вычислены k строк экстраполяционной таблицы, то для симметричных опорных методов имеем в качестве аппроксимации наивысшего порядка точности, равного 2k, при этом точность аппроксимации составит – (2k - 2). Для получения множества шагов интегрирования используется числовая последовательность: , позволяющая воспользоваться свойством симметричности [3].

Достоинство этого метода состоит в том, что он дает полную таблицу результатов вычислений, которые образуют последовательность вложенных методов, и позволяют оценить локальную погрешность, выбрать стратегию для методов переменного порядка. В таблице (1) – есть приближенное решение задачи Коши, полученное численным методом порядка с шагом

Экстраполяционные методы имеют то преимущество, что у них на каждом шаге можно менять не только длину шага, но и порядок метода. Следовательно, экстраполяцию можно рассматривать как метод с переменным порядком (столбцы таблицы) и переменным шагом интегрирования (строки таблицы).

Потенциально вычисления по технологии локальной экстраполяции содержат три источника внутреннего параллелизма:

• системный параллелизм (ограничен размерностью СОДУ).
• параллелизм экстраполяции (ограничен размерностью таблицы экстраполяции).
• параллелизм опорного метода (малая степень параллелизма).

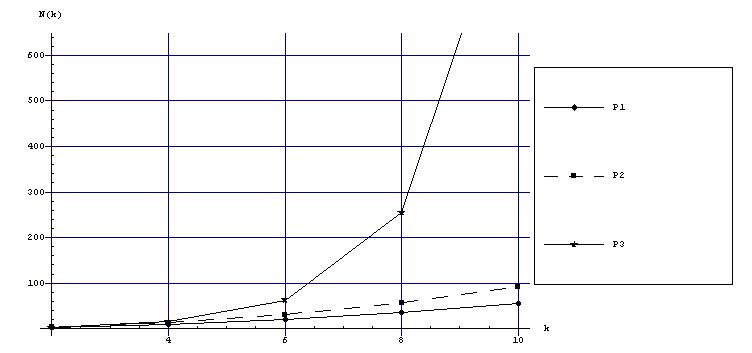
Поскольку в основу вычислений положена явная численная схема, реально имеется возможность использовать системный и экстраполяционный параллелизм.

Для получения множества шагов интегрирования рассмотрим числовые последовательности, образованные гармоническим рядом, степенями двойки, четными рядами чисел [Х]:

Эффективность использования последовательностей натуральных чисел для расчета шагов интегрирования в методе локальной экстраполяции можно оценить по графикам рисунка 4, где показана зависимость накладных расходов на формирование сеток интегрирования от длины экстраполяционной таблицы. При одном и том же опорном методе наиболее затратной является последовательность , которая фактически повторяет процесс удвоения шага, а наиболее эффективными являются последовательности и . Выбор опорного метода интегрирования базируется на исследовании влияния порядка метода и его свойств на объем необходимых вычислений. Пусть опорный метод имеет порядок – , длина экстраполяционной таблицы равна k, а число стадий явного метода – s, определим необходимый размер экстраполяционной таблицы для получения решения методом порядка r.

Рис.4 Накладные расходы при использовании числовых последовательностей от числа строк экстраполяционной таблицы для произвольного опорного метода

Суммируя все полученные результаты, можно сделать вывод, что для уменьшения накладных расходов при применении технологии локальной экстраполяции, следует выбирать опорный метод малого порядка, в частности второго, но с достаточными свойствами устойчивости. Однако, есть еще один момент требующий анализа. Теоретически нет никаких ограничений на длину экстраполяционной таблицы, но конечность памяти машины и накапливание ошибок округления, ограничивают длину экстраполяционной таблицы сверху и, как правило, используется . Поэтому, для получения высокоточного решения не имеется другой возможности получить решение, как использовать технологию Ричардсона на базе опорного метода высокого порядка.

Общая схема алгоритма локальной экстраполяции:

1. определяется размерность экстраполяционной таблицы на основе требуемого порядка экстраполяционного метода;
2. в соответствии с используемым типом параллелизма распределяются данные между процессорами;
3. вычисляется начальное приближение, на основе опорного метода (первый столбец экстраполяционной таблицы);
4. вычисляются значения экстраполяционной таблицы по формуле Эйткена-Невилла;
5. выполняются необходимые пересылки данных между процессорами через управляющий процессор в силу особенностей выбранной топологии.

Выводы

Сравнительный анализ динамических характеристик параллельных алгоритмов локальной экстраполяции на основе явных методов Рунге-Кутты показал, что областью приложений ЛЭР является высокоточное решение, сложная правая часть и многомерные задачи, однако требуется тщательный учет всех составляющих параллельной системы для того, чтобы такое решение было эффективным. Планируется провести исследования с использованием разных топологий, варьированием числовых последовательностей для генерации сеток интегрирования, а также применением неявных опорных методов, пригодных для решения жестких задач. Полученные результаты будут использованы при разработке библиотеки параллельного численного анализа для кластера WCCS-2003 Донецкого национального технического университета.

Литература

1. Хайрер Э., Нерсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи.– М.: Мир, 1990. – 512с.
2. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи: Пер. с англ. – М.: Мир, 1999. – 685с.
3. Холл Дж.,Уатт Дж. Современные численные методы решения обыкновенных дифференциальных уравнений. – М.: Мир, 1999. – 311с.
4. Вержбицкий В.М. Основы численных методов. – М.: Высшая школа, 2002. – 840с.
5. Арушанян О.Б., Залеткин С.Ф. Численное решение обыкновенных дифференциальных уравнений на Фортране.– М.: МГУ,1990.–336с.
6. Foster I. Designing and Building Parallel Programs. – Addison-Wesley, 1999. – 302 с.
7. Немнюгин С.А., Стесик О.Л. Параллельное программирование для многопроцессорных ВС. – СПб.: БХВ-Петербург, 2002. – 400 с.
8. Гергель В.П., Стронгин Р.Г. Основы параллельных вычислений для многопроцессорных вычислительных машин. – Нижний Новгород: Изд-во ННГУ им. Н.И.Лобачевского, 2000. – 176с.
9. Арушунян О.Б., Залеткин С.Ф., Калиткин Н.Н. Тесты для вычислительного практикума по обыкновенным дифференциальным уравнениям.// Вычислительные методы и программирование, 2002, т.3, c.11-19.
10. Thomas Rauber, Gudula Runger Lecture Notes in Computer Science 817 [Електронний ресурс]: http://citeseerx.ist.psu.edu/viewdoc/download&rep=rep1&type=pdf