Реферат по теме выпускной работы

Содержание

1. Введение.

2. Общие положения анализа устойчивости узлов нагрузки при малых возмущениях.

3. Основные математические соотношения для анализа статической устойчивости узлов нагрузки.

3.1. Расчет устойчивости асинхронных и синхронных двигателей.

3.2. Учет влияния электрической сети.

4. Учет влияния компенсации реактивной мощности.

5. Выводы.

6. Список использованных источников.

1 Введение

Определение условий устойчивости электрической нагрузки энергосистем является одним из необходимых этапов общего анализа энергосистем, определение пропускной способности линий электропередач, выбор средств управления, регулирования и т.д.. Такие исследования выполняются как на различных этапах проектирования, так и при эксплуатации - главным образом для уточнения области допустимых режимов.

Расчеты устойчивости нагрузки необходимы при проектировании систем электроснабжения промышленных предприятий для разработки мер, обеспечивают непрерывность технологичность процессов в различных режимах работы предприятий и при различных возмущениях.

Исследование устойчивости энергетических систем в общем случае предполагает анализ устойчивости статической или динамической как генераторов, так и двигателей. В энергосистемах возможны случаи, когда нарушение устойчивости генераторов не приводит к нарушению работы двигателей. В то же время возможны системные ситуации, которые вызывают торможение и последующее отключение больших групп двигателей при сохранении параллельной работы генераторов. Поэтому задача обеспечения устойчивости двигателей очень актуальна.

Целью работы является анализ статической устойчивости промышленных потребителей с двигательной нагрузкой при наличии синхронных и асинхронных двигателей.

Для исследования цели работы были поставлены и решены следующие задачи:

• разработка программного обеспечения для изучения теоретических положений вторичных критериев статической устойчивости;

• разработка программного обеспечения для выполнения расчетов по определению условий статической устойчивости методом малых колебаний;

• разработка методических указаний для создания лабораторной работы по изучению условий статической устойчивости более простой электрической системы.

Особенностью расчетов устойчивости узлов нагрузки является применение ЭВМ с использованием соответствующих математических моделей. Математическое описание двигательной нагрузки складывается в зависимости от числа двигателей, включенные в узле. Надо различать три основных случая [7].

1. Небольшая группа двигателей. Двигатель вводиться в расчет непосредственно: каждый из них учитывается своими уравнениями и параметрами.

2. Группы из многих двигателей, обслуживающих одно производство. Такие группы заменяют небольшим количеством двигателей.

3. Мощные узлы нагрузки. Их описание для расчетов устойчивости составляется на основе конкретных данных о составе нагрузки и параметров распределительной сети с использованием некоторых параметров, полученных путем статистического анализа.

Использование на промышленных предприятиях полупроводниковых преобразователей, дуговых печей прямого нагрева для плавки стали, электросварочных установок вызывают большое потребление реактивной мощности. Поэтому при анализе электромеханических переходных процессов необходимо учитывать влияние реактивной мощности на устойчивость узлов электрических нагрузок.

В практике исследования устойчивости узлов нагрузки применяемые комплексные расчетные модели [4] описывают простую одноузловую схему. Такие модели позволяют воспроизвести основные особенности переходных процессов в электродвигателях и учесть влияние других электроприемников.

Комплексные расчетные модели нагрузки содержат уравнения эквивалентных асинхронного и синхронного двигателей, а также статической нагрузки. Под статической нагрузкой понимают нагрузку, которая не имеет магнитных полей, вращающихся: освещение, электропечи, коммунально-бытовые приборы, конденсаторные батареи, индуктивные и активные сопротивления элементов сети.

2 Общие положения анализа устойчивости узлов нагрузки при малых возмущениях

Малые возмущения могут возникать под действием системы питания (изменение напряжения и частоты), а также вследствие изменения работы самой системы и ее электропотребителей по условиям технологического процесса (изменение количества линий питания, оперативные переключения и т.п.). В таких условиях электроснабжения свойства и тип электроприемников узла нагрузки существенно влияет на его устойчивость.

Статическую устойчивость узла промышленного нагрузки рассчитывают в такой последовательности [1]:

- Заменяют узел нагрузки расчетной моделью и определяют ее параметры;

- Выделяют существенные параметры и критерии устойчивости для данной схемы электроснабжения;

- Оценивают допустимый режим по критическому значению существенных переменных запасом устойчивости.

Узел нагрузки с асинхронными двигателями замещают расчетной моделью в виде эквивалентного асинхронного двигателя. Погрешность замещения зависит от способа ее осуществления [3]. Выбор критерия замещения зависит от цели задачи, которая решается, и необходимой точности. В приближенных расчетах можно использовать статистические параметры эквивалентного двигателя.

Разнотипность синхронных двигателей в узлах нагрузки невелика. Это позволяет учитывать их по фактическим параметрам и параметрам нормального режима. В приближенных расчетах устойчивости узлов нагрузки используют средние значения параметров синхронных двигателей. Они отличаются в зависимости от типа двигателей (явнополюсный,  неявнополюсный).

Узел нагрузки, где есть асинхронные и синхронные двигатели, представляющие комплексной расчетной моделью. Ее параметры можно установить замещением отдельных характерных составляющих нагрузки, которые описываются статическими характеристиками. Для приближенных расчетов можно использовать средние значения параметров модели, которые приведены в [1].

Устойчивость узла нагрузки анализируют в схеме замещения всей системы электроснабжения и параметрами ее режима. В зависимости от конкретных условий расчетную схему электроснабжения сводят к одному из основных видов, приведенных на рис. 1.

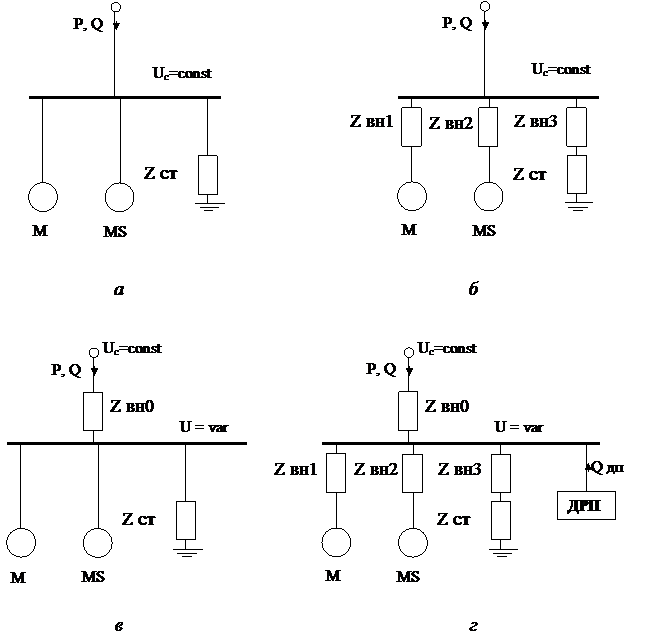
Рисунок 1 - Расчетные модели узла нагрузки

Это дает возможность использовать практические критерии устойчивости. Таким образом, получают четыре расчетных моделей узла нагрузки, которые отличаются между собой критериями устойчивости [2]:

1. Модель, где напряжение в узле нагрузки является независимой переменной, которая не зависит от режима работы электроприемников, что позволяет рассчитывать устойчивость независимо для каждой из характерных групп электроприемников по основному критерию (рис. 1 а).

2. Модель, где характерные группы электроприемников радиально связанные с помощью внешнего сопротивления с шинами узла нагрузки, напряжение на которых является независимой переменной режима (рис. 1, б).

3. Модель, где характерные группы электроприемников соединены с узлом нагрузки с помощью внешнего сопротивления и независимым переменным режима является э.д.с. источника питания (рис. 1, в).

4. Модель, где узел нагрузки содержит все характерные составляющие, а также источник реактивной мощности (ИРМ) (рис. 1, г).

3 Основные математические соотношения для анализа статической устойчивости узлов нагрузки

3.1 Расчет устойчивости асинхронных и синхронных двигателей

Нарушение статической устойчивости в своей начальной стадии может характеризоваться меняющимся (апериодическим) изменением параметров режима, например, увеличением угла нагрузки, если мощность, приводного механизма превышает максимальное значение. При некоторых условиях возможно также нарушение статической устойчивости при возникновении и росте колебаний параметров режима (колебательное возбуждение). Основными причинами, которые вызывают нарушения апериодического типа является рост мощности, значительное увеличение внешнего сопротивления и чаще всего снижение напряжения в узле нагрузки. Конечно, запас по статической устойчивости нагрузки оценивается величиной допустимого снижения напряжения в точке питания при нормальном состоянии сети [8].

Значение напряжения на зажимах двигателей и независимым от режима работы двигателей э.д.с. источники питания называются критическими (), если они соответствуют границе апериодической устойчивости. Критический режим для синхронного двигателя, связанного с источником э.д.с. постоянным сопротивлением, определяются следующим выражением

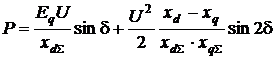
Независимая оценка устойчивости узла нагрузки по отдельным группам асинхронных и синхронных двигателей выполняется для расчетных моделей согласно рис. 1 а и б. Существенной независимой переменной в этом случае является напряжение на шинах узла нагрузки. Для оценки его устойчивости используют главные критерии устойчивости:

   и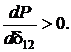  

При этом необходимо учитывать характеристики представленных механизмов и их загрузки.

Для асинхронных двигателей (или их эквивалента) главным требованием нарушения устойчивости является граничное уравнение. При Ммх=соnst  и непосредственным включением двигателей к шинам узла нагрузки критические параметры, соответствующие граничному режиму его статической устойчивости, определяются по формулам:

При включении двигателей к узлу нагрузки через собственные внешние сопротивления zвн.1, zвн.2 і zвн.3 (см. рис. 1, б) расчет предельных параметров режима и запаса устойчивости выполняется аналогично с учетом этих сопротивлений.

Если активными сопротивлениями пренебрегать, то расчетные формулы в таком случае имеют вид:

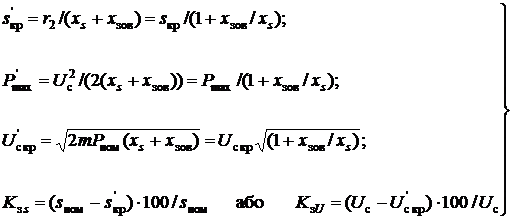 (1)

Наличие внешнего сопротивления при включении к узлу нагрузки асинхронных двигателей снижает пороговое по статической устойчивостью значение скольжения.

При известной характеристике представленного механизма Ммх = f (s) пороговые параметры режима находят при решении системы уравнений:

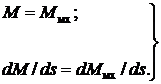 (2)

С учетом выражения для расчета предельного скольжения

и системы уравнений (1) после соответствующих преобразований система уравнений (2) принимает вид:

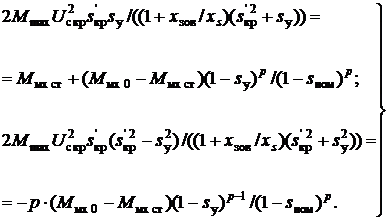  (3)

Рассчитав систему уравнений (3), можно определить параметры Uскр и Sу для предельного по устойчивости режима, где соответствующее границе статической устойчивости скольжения Sу будет больше предельного скольжения при М < Mmax / (1+xзов / xs).

В приближенных расчетах считают . Тогда после решения системы уравнений (3) получаем

  (4)

При p = 0 имеет место особый случай  и выражение для определения критического напряжения превращается в соответствующее выражение, получаемый из (1).

Критическое напряжение на выводах двигателя определяется при допущении равенства тока статора  и сводного тока ротора . Поскольку

, 
а с учетом (1)

,

 выражение для определения критического напряжения на зажимах двигателя можно записать в следующем виде:

 . (5)

Статическая устойчивость синхронных двигателей, подключенных к узлу нагрузки с неизменным значением напряжения и частоты, нарушается при граничном условии . С учетом

 и

 это условие можно представить в следующем виде:

 . (6)

 При отсутствии устройств АРВ двигателей производная и предельный за статической устойчивостью режим соответствует значению угла , когда

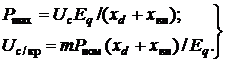 (7)

 Электродвижущая сила  в долях ее значение при холостом ходу определяется выражением

 ,(8)

 где ;   .

  

 При наличии автоматического регулятора пропорциональной действия синхронный двигатель и генератор можно представить в виде переходного сопротивления  и ЭДС . В этом случае критическое напряжение на зажимах двигателя определяется зависимостью

 (9)

 и всегда менее критического напряжения, которое определяется выражением (7) При отсутствии АРВ, поскольку переходное сопротивление значительно меньше синхронного.

Присутствие внешнего сопротивления при подключении к узлу нагрузки асинхронных и синхронных двигателей снижают предельное по статической устойчивостью значение максимальной активной мощности и повышают значение критического напряжения в узле нагрузки. Это, в свою очередь, делает более жесткими требованиями к стабильности напряжения питания.

3.2 Учет воздействия электрической сети

Если двигатели узла нагрузки присоединены к центру питания с постоянным напряжением через внешнюю сеть (см. рис.1, в), то условия устойчивости узла нагрузки существенно зависят от параметров этой сети с сопротивлением и режима работы всех электроприемников. В этом случае напряжение в узле нагрузки является переменной величиной и ее значение будет зависеть от изменения упомянутых факторов. Поэтому устойчивость узла нагрузки оценивают на основе независимой переменной - напряжения в узле нагрузки. При этом используются побочные критерии

 (10)

или

. (11)

 При использовании критерия (10) Переменные режима можно аналитически связать между собой, применив статические характеристики узла нагрузки  и :

 

 . (12)

 Исследование этого выражения в области значений функций (10) и (11) имеют целью определить координаты  и минимума функции, соответствующие пределы статической устойчивости .

Согласно критерию (11) Статическую устойчивость оценивают при нарушении в узле нагрузки баланса реактивной мощности, который вызывается снижением напряжения. Для точки уравновешенности режима должно выполняться условие баланса , а в ее окресности – неравенство .

Метод исследования изменения реактивной мощности

 (13)

 выбирают в зависимости от исходной информации о узле нагрузки. Если известны статические характеристики нагрузки, то условия статической устойчивости определяют аналитически. В противном случае статической устойчивости анализируют графическим исследованием выражения

 (14)

 по зависимостям составляющих от напряжения в узле нагрузки.

Цель графического анализа - определить статическую устойчивость режима по условию .

Составляющие небаланса реактивной мощности (14) определяют следующим образом.

Зависимость реактивной мощности, которая поступает от электрической системы, от напряжения в узле нагрузки определяется уравнением

 . (15)

 Реактивную мощность, потребляемую эквивалентным асинхронным двигателем, можно рассчитать по формуле

 , (16)

где . (17)

Если соотношение  и  при условии неизменности частоты заменить их значения:

;

,

 то получаем выражение для определения реактивной мощности через напряжение в узле нагрузки:

,

 или

 . (18)

 На границе статической устойчивости  и . При этом критическое значение напряжения на выводах асинхронного двигателя определяется выражением

 , (19)

 а критическое значение потребляемой им реактивной мощности - выражением

 . (20)

 Последнее выражение с учетом (17) можно упростить:

 . (21)

 Устойчивость синхронных двигателей обычно анализируют без учета насыщения и асимметрии ротора.

Реактивную мощность синхронного двигателя рассчитывают по выражению

 , (22)

 где  - ЭДС холостого хода, которая обусловлена ​​током возбуждения и определяется следующим выражением:

 . (23)

 Если , то двигатель потребляет из сети реактивную мощность, при  он работает в режиме ; если , то двигатель генерирует реактивную мощность в сеть.

При нагрузке синхронного двигателя ЭДС статора, которая образуется результирующим магнитным потоком в его воздушном зазоре, можно определить по формуле

 , (24)

 где  - сопротивление рассеяния двигателя (в практических расчетах можно принимать для явнополюсных двигателей ).

Реактивная мощность, которую генерирует синхронный двигатель, зависит от отношения короткого замыкания и кратности изменения тока возбуждения. Это отношение является конструктивным параметром двигателя и в расчетах принимают . Связь тока возбуждения с существенной переменной (напряжение сети) при анализе устойчивости узла нагрузки определяется структурой системы возбуждения синхронного двигателя.

При отсутствии регулирования возбуждения и при питании обмотки возбуждения от машинного возбудителя ток возбуждения не зависит от напряжения сети.

При питании обмотки возбуждения от выпрямителей и отсутствия АРВ ток возбуждения практически пропорционально зависит от напряжения сети.

При наличии АРВ ток возбуждения увеличивается при снижении напряжения на обмотке статора двигателя.

Зависимость ЭДС статора от тока возбуждения СД определяется выражением

 , (25)

 где  - коэффициент, характеризующий степень насыщения обмотки статора (в расчетах без учета насыщения;  - ток возбуждения холостого хода;  - номинальный ток возбуждения;  - кратность тока возбуждения, обусловленная системой возбуждения;  - тоже при холостом ходе двигателя.

При изменении тока возбуждения изменяется реактивная мощность СД по выражению

. (26)

 Зависимость (26) можно использовать для анализа реактивной мощности СД в функции напряжения на его выводах, если известен закон регулирования возбуждения .

Для границы статической устойчивости узла нагрузки критическое напряжение на выводах СД с учетом (7) и при регулировании тока возбуждения в соответствии с (25) определяется выражением

 . (27)

 После подстановки этого выражения в уравнение (26) получаем

 . (28)

 Из уравнения (28) следует, что на границе статической устойчивости узла нагрузки синхронный двигатель потребляет из сети реактивную мощность.

4 Учет влияния компенсации реактивной мощности

 К узлу нагрузки реактивная мощность поступает с электрической системы. Но она может генерироваться и местными источниками реактивной мощности (ИРМ). Такими ДРП могут быть конденсаторные батареи, синхронные компенсаторы, синхронные двигатели (рис. 1, г).

Реактивная мощность конденсаторной батареи существенно зависит от напряжения в узле и может быть определена следующим образом

, (29)

где  - номинальная мощность конденсаторной батареи; С - результирующая емкость батареи.

Синхронный компенсатор или синхронный двигатель могут генерировать и потреблять реактивную мощность, которая определяется выражением

, (30)

Режим работы синхронного компенсатора задается системой его возбуждения.

Главное назначение местных источников реактивной мощности - разгрузка сети питания и распределение от перетоков реактивной мощности. Батарея конденсаторов может устанавливаться в любой точке электрической сети. Синхронные компенсаторы располагают в мощных узлах нагрузки с напряжением 6-10 кВ. Это обычно соответствует районной подстанции электрической системы. Благодаря местным ДРП снижаются потери энергии в электрической сети, повышается уровень и качество напряжения у потребителей и изменяются условия устойчивости узла нагрузки.

В оценке устойчивости узла нагрузки с компенсирующими устройствами реактивной мощности существенными факторами является расположение этих устройств в узле асинхронного нагрузки и использования в узлах комплексной нагрузки.

При размещении ДРП в узле асинхронной нагрузки изменяются условия внешнего электроснабжения. В результате этого напряжение в электроприемниках из-за уменьшения падения напряжения в сети питания повышается. Падение напряжения определяется выражением

. (31)

 Изменение эквивалентных параметров внешней сети при включении конденсаторной батареи можно определить следующим образом:

, (32)

. (33)

 То есть осуществляется увеличение напряжения в электроприемниках узла нагрузки и сопротивления связи узла с шинами бесконечной мощности, что приводит к соответствующему изменение критических параметров:

критическое скольжение (1) уменьшается до значения

, (34)

а критическое напряжение увеличивается до значения

. (35)

Как видим это соответствует уменьшению запасов статической устойчивости узла нагрузки. При этом условие устойчивости узла нагрузки по активной мощностью зависит от соотношения сопротивлений .

Повышение мощности конденсаторной батареи негативно сказывается на устойчивости узла асинхронного нагрузки, поскольку при этом падает .

Если узел комплексной нагрузки удален от источника неизменного напряжения и содержит местный ДРП (см. рис. 1, г), то статическую устойчивость такого узла необходимо анализировать по критерию (11). В этом случае уравнения небаланса реактивной мощности в узле имеет вид

 . (36)

Исследования (36) на экстремум выполняется графически.

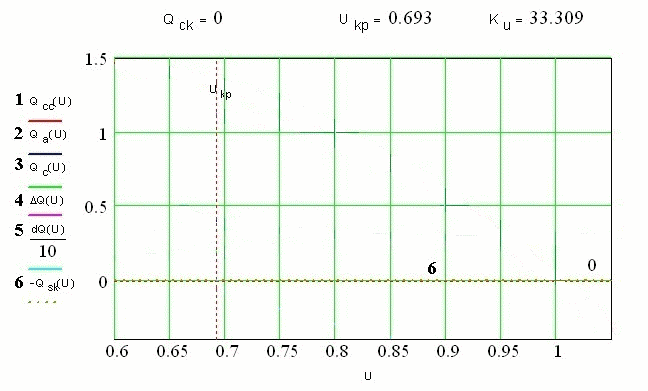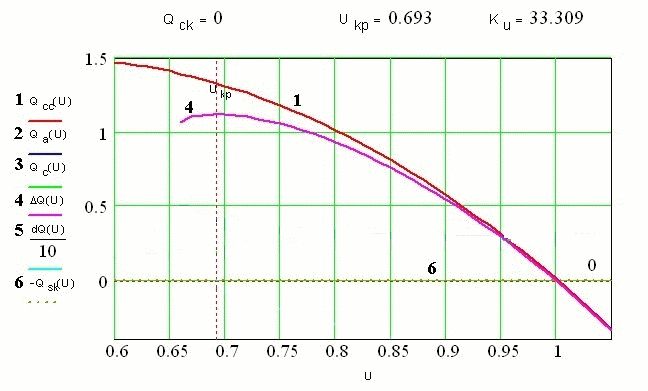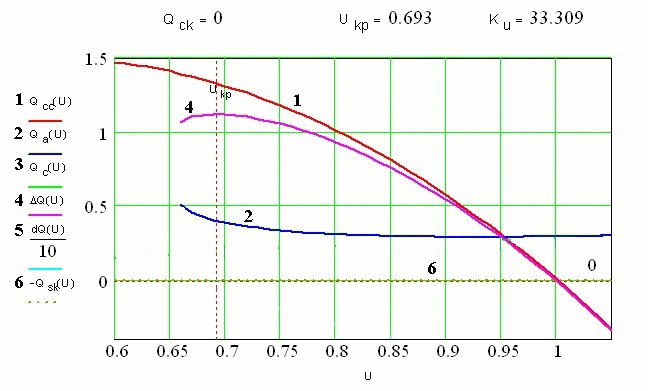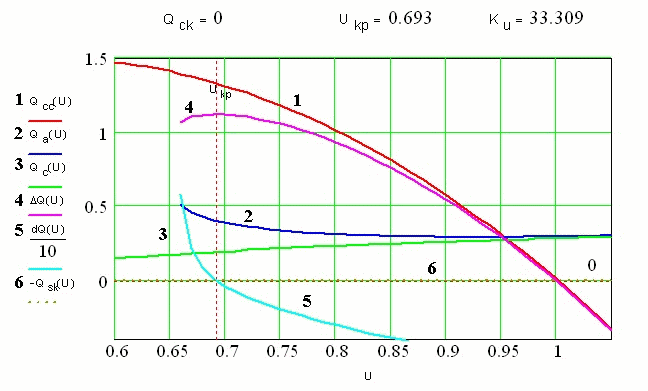
Рисунок 2 - Определение критического напряжения узла нагрузки без учета мощности компенсирующих устройств

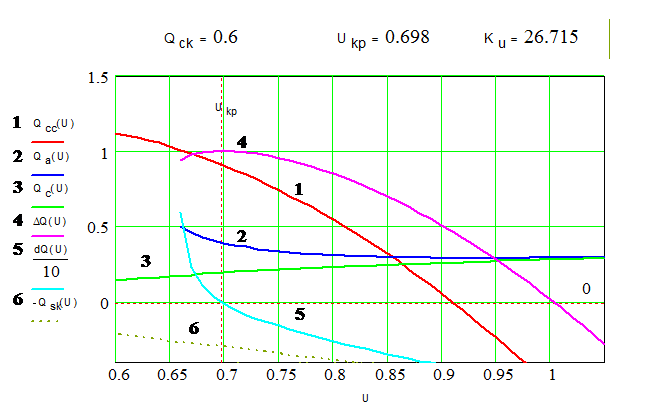
Рисунок 3 - Определение критического напряжения узла нагрузки с учетом мощности компенсирующих устройств

 суммарная характеристика реактивной мощности нагрузки и ДРП становится более пологой.

5 Выводы

 В данной магистерской работе рассматриваются методики оценки статической устойчивости всех упомянутых расчетных моделей узла нагрузки. В среде универсального математического процессора MathCAD 7.0 Разрабатывается программное обеспечение для проведения конкретных расчетов. С помощью разработанных программ выполняются расчеты статической устойчивости по различным критериям узла нагрузки подстанции "Авдеевка - 35". На данном этапе магистерская работа не завершена.

6 Перечень использованной литературы

 1. Рогозин Г.Г. Об использовании функциональных характеристик при учете влияния насыщения синхронных машин / Г.Г. Рогозин, И.И. Ларина / / Изв. АН СССР. Энергетика и транспорт. - 1986. - № 6. - С.61-68.

 2. Машины электрические синхронные Трехфазные. Методы испытания. ГОСТ 10169-77. М.: Госкомстандарт СМ СССР, 1977.

 3. Казовский Е.Я. Переходные процессы в электрических машинах переменного тока. - М.: Изд-во АН СССР, 1962. - 624 с.

 4. Шапиро А.С. Схема замещения турбогенератора при больших скольжения с учетом клиньев и торцевого эффекта / / Турбо-и гидрогенераторы большой мощности и перспективы их развития. - Л.: Наука, 1969. - С. 153-167.

 5. Переходные процессы в системах электроснабжения: Учебник / В. Н. Винославский, Г.Г. Пивняк, Л.И. Несен и др.; Под ред. В. Н. Винославского. - М.: Выща шк. Головное изд-во, 1989. - 422 с.: Ил.

 6. Методические указания к лабораторным работам по электромеханическим переходным процессам в электрических системах (для студентов специальностей 1001, 1002, 1004.01) / Сост.: Г. Г. Рогозин, А. М. Ларин, Н. Г. Пятлина. - Донецк: ДПИ, 1990. - 48 с.

 7. Переходные электромеханические процессы в электрических системах: Учеб. для электроэнергет. спец. вузов. - 2-е изд, перераб. и доп. В. А. Венников / М.: Высш. шк, 1970. - 472 с, ил.

 8. Жданов П. С. статическая устойчивость сложных электрических систем. - М.: 1940,

 9. Кафедра ЭСИС — разработка автоматизированной системы управления электрическим системами [Электронный ресурс].— Режим доступа: http://etf.donntu.ru

 10. Методы расчетов предельных по статической устойчивости режимов энергосистем [Электронный ресурс].— Режим доступа: http://referats.allbest.ru/programming/103021.html