Мишустин Сергей Михайлович

Введение

В последние годы интенсивно разрабатывается научное направление с названием «Естественные вычисления» (Natural Computing), объединяющее математические методы, в которых заложены принципы природных механизмов принятия решений. Эти механизмы обеспечивают эффективную адаптацию флоры и фауны к окружающей среде на протяжении нескольких миллионов лет.

Из наших современников областью естественных вычислений занимаются С. Янг, Г. Бени , Дж. Ванг, М. Дориго, а также отечественные исследователи С.А. Субботин, А.А. Олейник, В.К Яценко и многие другие.

Примерами алгоритмов, основанных на естественных вычислениях, являются: алгоритм муравьиных колоний, алгоритм оптимизации на основе перемещения бактерий, алгоритм роя частиц, а также генетический алгоритм.

Одной из областей применения таких алгоритмов является область распознавания образов, которая в наше время широко применяется для распознавания жестов, в том числе и на устройствах с multitouch интерфейсами.

В основе создания современных multitouch интерфейсов лежит алфавит жестов на плоскости. Математическая модель этих жестов представляет собой двумерные формы объектов. Например, дуга может являться жестом вращения, прямая – масштабирования или перемещения.

Для наилучших результатов распознавания используются многоагентные системы. Многоагентной системой в данном случае может выступать как алгоритм, использующий множество агентов, например: алгоритм муравьиной колонии, пчелиный алгоритм или алгоритм оптимизации на основе перемещения бактерий, так и система, состоящая из нескольких алгоритмов, где алгоритмы некоторым образом взаимодействуют между собой.

В муравьином алгоритме, колония муравьев также может рассматриваться как многоагентная система, в которой каждый агент (муравей) функционирует автономно по очень простым правилам. В противовес почти примитивному поведению агентов, поведение всей системы получается на удивление разумным.

Муравьиные алгоритмы серьезно исследуются европейскими учеными с середины 90-х годов. На сегодняшний день уже получены хорошие результаты для оптимизации таких сложных комбинаторных задач, как задача коммивояжера, задача оптимизации маршрутов грузовиков, задача раскраски графа, квадратичная задача о назначениях, задача оптимизации сетевых графиков, задача календарного планирования и многие другие.

Особенно эффективны муравьиные алгоритмы при динамической оптимизации процессов в распределенных нестационарных системах, например, трафиков в телекоммуникационных сетях.

Генетический  алгоритм (ГА) сам по себе не являются многоагентной системой, но для решения ряда задач является довольно эффективным. В  основе  ГА  лежат  принципы  естественной  эволюции,  сформулированные Дарвином, – естественный отбор, изменчивость, наследственность. С их помощью  ГА  моделируют  генетические  процессы,  происходящие  в  биологических сообществах.

Обычно  генетические  алгоритмы  применяются  для  решения оптимизационных  задач.  Предметная область  ГА  включает  в  себя  проблемы комбинаторики,  биоинформатики и др.  ГА  применяются  также  для обработки и распознавания образов, в частности изображений.

Еще один алгоритм – оптимизация на основе моделирования перемещения бактерий (BFO) была принята научным сообществом в качестве глобального алгоритма оптимизации для распределенной оптимизации и управления. BFO основывается на моделировании поведения кишечной палочки. BFO уже привлек внимание исследователей из-за своей эффективности в решении реальных задач оптимизации, возникающих в нескольких областях применения. Биологическая основа стратегии – перемещение бактерий E.coli, эмулируется удивительным образом и используется как простой алгоритм оптимизации.

Целью выполнения данной научной работы является анализ существующих эвристических алгоритмов, применяемых в задачах распознавания образов. Анализ проводится в контексте распознавания форм двумерных объектов, которые могут быть получены с устройств использующих технологию multitouch.

1. Цель и задачи исследования, планируемые результаты

Объектом исследования является бинарное изображение.

Предметом исследования является эволюционный метод поиска форм двумерных объектов на заданном изображении.

Основной задачей является исследование, разработка и программная реализация эволюционного метода поиска форм двумерных объектов на бинарном изображении.

2. Актуальность темы

Распознавание простых геометрических фигур на изображениях очень распространено в ряде задач, потому что такие фигуры часто присутствуют в среде, созданной человеком. Для этой задачи в последнее время открылась еще одна область – мобильные сенсорные устройства. В некоторых приложениях и играх требуется распознавать примитивные фигуры, считанные с экрана в результате проведения по нему манипулятором.

3. Предполагаемая научная новизна

Предполагается, что скорость поиска при работе разработанного метода или разработанной модификации существующего метода будет выше, чем у методов распространенных на данный момент, за счет выполнения только одной итерации поиска.

4. Обзор существующих методов распознавания

Одним из самых распространенных среди детерминированных методов является метод преобразований Хафа (HT), который зачастую требуют объемных вычислений и затрат памяти. Чтобы преодолеть эти ограничения, исследователи предложили новые подходы к HT, например, вероятностный HT, рандомизированный HT и нечеткий HT. Эффективность использования преобразований Хафа резко падает при увеличении размерности фазового пространства. Преобразование Хафа можно применить для любой фигуры, форма которой полностью определяется некоторым набором параметров, например прямоугольника, треугольника, и т.д [1].

Как альтернатива основанным на HT методам, задача распознавания формы решалась  методами стохастического поиска. Стохастические алгоритмы, подобно генетическим алгоритмам (GA), показывают хорошие результаты поиска оптимальных решений из-за обладания большим количеством неявного параллелизма.

В 2002 году был предложен мощный алгоритм оптимизации, теперь известный как алгоритм оптимизации, основанный на передвижении бактерий (BFOA). Он представляет собой многоагентную систему. BFOA имитирует отдельное и сгруппированное поведение бактерий, живущих в кишечнике большинства млекопитающих. С помощью этого алгоритма существует возможность обнаруживать формы, если адаптировать его для этой задачи.

Для задачи распознавания простых фигур выбран алгоритм BFOA, так как для нахождения им различных фигур достаточно заменить функцию определения оптимальности особи и в зависимости от фигуры будет изменено пространство поиска.

5. Описание работы алгоритма BFOA для распознавания окружности

Каждый предполагаемый круг представлен позицией бактерии, где первые два компонента вектора, х и у – координаты центра этой окружности, а третий компонент r – радиус.

Пусть (x_k,y_k,r_k) будет k-м тестовым кругом популяции, где k = 1,…,S, где S - это размер популяции, т.е. обозначает общее количество тестовых кругов. В фазе инициализации случайные значения в подходящем диапазоне присвоены каждой из трех координат векторов. Давайте рассматривать 2N равномерно распределенных демонстрационных точек на круге. На рис. 1 показан случай, когда N=4.

Предположим, что искомая окружность располагается на некотором изображении. Функция P(x,y) равна 1, если пиксель (x,y) является граничным, 0 – иначе. Пусть A будет граничной матрицей. Целевую функцию обозначим как J. Пусть для (x₀,y₀,r₀) тестового круга ее значение будет J₀ = J(A, x₀, y₀, r₀).

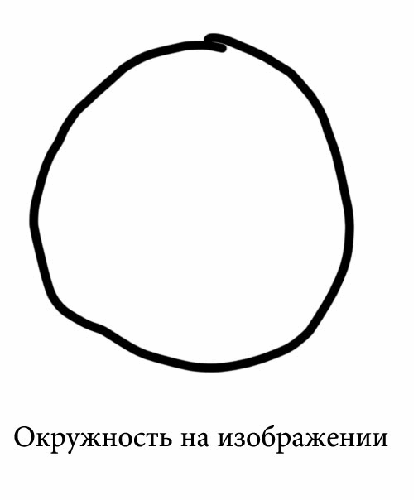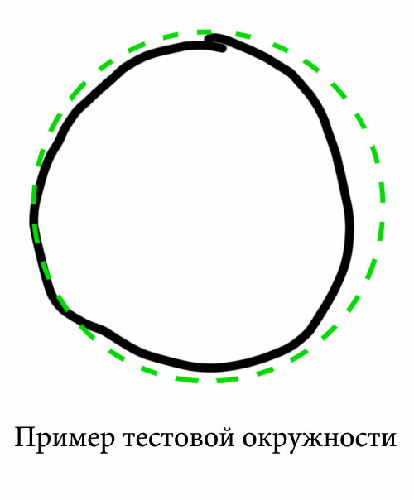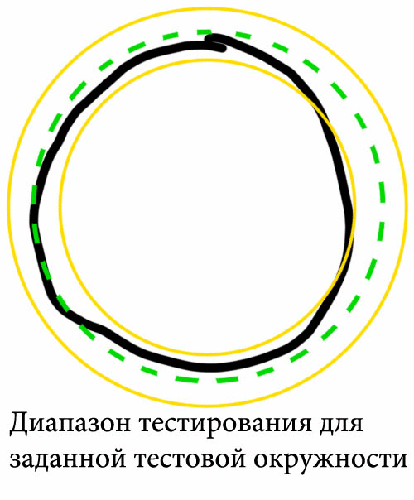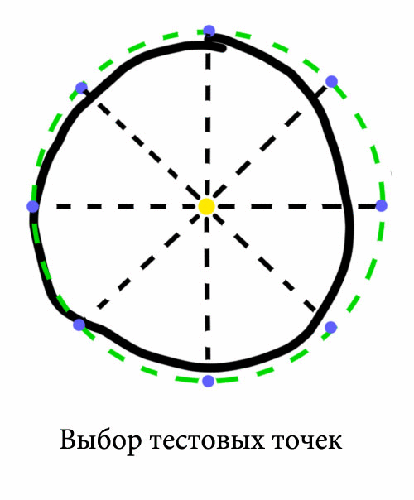
Рисунок 5.1 – Окружность с демонстрационными точками, изображенными синим (анимация: 4 кадра, 7 циклов повторения, 99 килобайт)

 

Для определения является ли кандидат кругом можно рассмотреть множество кругов с центром в (x₀,y₀) и радиусом, варьирующимся в диапазоне от  до . Назовем это множество тестовой полосой. Значение  можно взять как процент от радиуса, предлагается . После этого N тестовых точек берутся для каждого круга в тестовом диапазоне. Тестовые точки расположены на круге на равном расстоянии друг от друга. Пусть i-я тестовая точка на тестовом круге имеет радиус  и обозначается .

          (5.1)

Рисунок 5.2 – Формула вычисления x для i-ой тестовой точки

          (5.2)

Рисунок 5.3 – Формула вычисления y для i-ой тестовой точки

где i = 1,2,…,N; j = -,,…0…,,.

Чтобы измерить степень принадлежности тестовой точки к окружности центрального круга определим функцию расстояния . Значение функции расстояния  для тестовой точки  определяется как:

          (5.3)

Рисунок 5.4 – Формула вычисления функции расстояния для i-ой тестовой точки

Значение  может изменяться в диапазоне от 0 до 1. Когда , это означает, что выбранная точка граничная и она находится на центральном круге. Если  не граничная точка то .

Целевая функция, соответствующая (x₀,y₀,r₀) для граничной матрицы A определяется по следующей формуле

          (5.2)

Рисунок 5.5 – Формула вычисления целевой функции

Целевая функция взвешивает каждую граничную точку согласно радиусу круга кандидата [3].

Таким образом, становится возможным с помощью алгоритма BFOA распознать окружность на изображении. Аналогичным образом можно подобрать параметры, которые идентифицируют любую другую фигуру, определить соответствующую этой фигуре целевую функцию и приведенный алгоритм можно будет использовать для поиска этой фигуры на изображении.

6. Существующая модификация для нахождения нескольких фигур на одном изображении

Предложенный алгоритм с некоторыми модификациями может обнаруживать множество фигур на одном изображении. Этого можно достичь, если задать верхний предел числа фигур. Метод выполняется на исходной граничной карте. Когда фигура найдена – она маскируется на граничной карте. Затем опять выполняем поиск. Процедура повторяется до тех пор, пока заданное количество фигур не будет найдено. В этом подходе есть возможность ложного обнаружения в случае, если фактическое число фигур меньше, чем определенное максимальное количество [3].

7. Описание работы алгоритма BFOA для распознавания произвольной формы.

Представим бактерию позицией предполагаемой формы в виде координат х и у, ее угла поворота a и масштаба s. Форма является массивом вершин относительно ее положения.

Пусть (x_k,y_ka_ks_k) будет k-ой тестовой формой  популяции, где k = 1,…,S, а S - это размер популяции, т.е. обозначает общее количество тестовых форм. При инициализации каждой из четырёх координат векторам присваиваются случайные значения в подходящем диапазоне. Рассмотрим N демонстрационных точек произвольной фигуры. На рис. 7.1 показан случай, когда N=10 для распознавания трапеции.

Предположим, что искомая форма располагается на некотором изображении. Функция P(x,y) равна 1, если пиксель (x,y) является граничным, 0 – иначе. Пусть A будет граничной матрицей. Целевую функцию обозначим как J. Пусть для (x₀,y₀a₀s₀) тестовой формы ее значение будет J₀ = J(A, x₀, y₀, a₀, s₀).

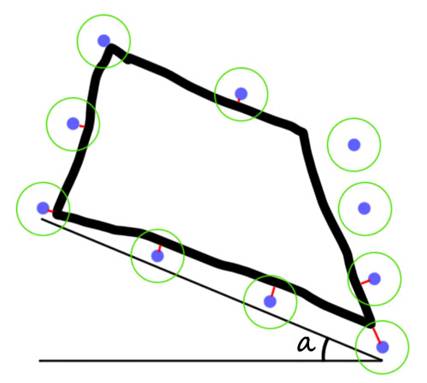
Рисунок 7.1 – Произвольная форма с демонстрационными точками, изображенными синим

Для определения является ли кандидат искомой формой нужно вычислить целевую функцию. Чем меньше значение целевой функции, тем более точно форма соответствует кандидату. Целевая функция вычисляется на основании суммы расстояний от тестовых точек к ближайшим граничным точкам, если таковые имеются.

Показатель r представляет собой радиус окружности вокруг тестовой точки, где будет производиться поиск граничной точки. В общем случае предлагается брать его следующим образом:

,          (7.1)

Рисунок 7.2 – Формула вычисления r

где .

На рис. 7.1 зеленым изображены круги с радиусом r вокруг тестовых точек.

Чтобы измерить степень принадлежности тестовой точки к форме на граничной матрице, определим функцию расстояния . Если существует такое k и l, что , то значение функции расстояния  для i-ой тестовой точки определяется как:

,          (7.2)

Рисунок 7.3 – Формула вычисления функции расстояния

где .

Иначе . Также , если результат вычислений по формуле (7.2) больше, чем r, где M – число больше единицы. Предлагается брать .

Значение  может изменяться в диапазоне от 0 до 1 или быть равно 2. Когда  находится в диапазоне от 0 до 1, это означает, что граничная точка находится на расстоянии  от тестовой точки. Если , это означает, что нет граничной точки, которая лежит ближе, чем на расстоянии r от тестовой.

На рис. 7.1 красным изображены  для тестовых точек.

Целевая функция, соответствующая (x₀,y₀a₀s₀) для граничной матрицы A определяется по следующей формуле:

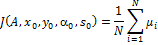          (7.3)

Рисунок 7.4 – Формула вычисления целевой функции

Таким образом, возможно распознавать произвольные формы на изображении.

8. Предлагаемая модификация для распознавания нескольких фигур на одном изображении

Предлагается альтернативный вариант нахождения нескольких фигур на одном изображении.

В качестве критерия останова алгоритма предлагается некоторое количество итераций алгоритма без улучшения суммарной целевой функции всех особей. Количество таких итераций необходимо определить экспериментально.

Размер популяции является одним из ключевых факторов данной модификации. Недостаточный размер популяции может привести к тому, что некоторые фигуры могут быть не найдены. С другой стороны, большой размер популяции сильно скажется на производительности алгоритма и скорости обнаружения фигур. Размер популяции должен быть определен экспериментально.

После отработки алгоритма необходимо применить любой из алгоритмов кластеризации для неизвестного количества кластеров к особям. Каждая особь с наилучшим значением целевой функции в кластере будет искомой фигурой, если значение ее целевой функции превышает некоторый порог, определенный экспериментально.

Выводы

Проведен обзор методов, которые могут быть применены для задачи распознавания простых фигур. Выбран метод распознавания для этой задачи. Обоснованы причины выбора. Рассмотрена работа алгоритма BFOA на примере распознавания окружности. Рассмотрена существующая модификация алгоритма BFOA для поиска нескольких фигур на изображении. Предложена модификация этого метода. Проведена сравнительная характеристика существующей и предложенной модификаций. В дальнейшем планируется исследование работы существующей и предложенной модификаций на различных изображениях для определения числовых характеристик скорости работы, а также планируется анализ различных целевых функций.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2013 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список источников

1.  Преобразование Хафа (Hough transform) [Електронний ресурс]. – Режим доступа : http://www.cgm.computergraphics.ru/content/view/36.

2.  Kim D.H., Abraham A., Cho J.H. A Hybrid Genetic Algorithm and Bacterial Foraging Approach for Global Optimization // Information Sciences. – 2007. – № 18 (177). – P. 3918-3937.

3.  S. Dasgupta, S. Das, A. Biswas, A. Abraham Automatic circle detection on digital images with an adaptive bacterial foraging algorithm // Soft Comput. – 2010. – P. 1151–1164.

4.  Генетический алгоритм [Електронний ресурс]. – Режим доступа : ru.wikipedia.org/wiki/Генетический_алгоритм.

5.  Neidhardt F.C., Ingraham J.L., Schaechter M. Physiology of the Bacterial Cell: A Molecular Approach. – Sunderland: Sinauer Associates, 1990. – 520 p.

6.  Alberts B., Bray D., Lewis J., Raff M., Roberts K., Watson J.D. Molecular Biology of the Cell. – New York: Garland Publishing, 1994. – 1408 p.

7.  Segall J.E., Block S.M., Berg H.C. Temporal Comparisons in Bacterial Chemotaxis // Proceedings of the National Academy of Sciences. – 1986. – № 83 (23). – P. 8987-8991.

8.  Berg H.C. Random Walks in Biology. – Princeton: Princeton University Press, 1993. – 164 p.

9.  Woodward D.E., Tyson R., Myerscough M.R., Murray J.D., Budrene E.O., Berg H.C. Spatio-Temporal Patterns Generated by Salmonella Typhimurium // Biophysical Journal. – 1995. – № 68. – P. 2181-2189.

10.  Analysis And Design of Intelligent Systems Using Soft Computing Techniques / Eds.: P. Melin, O.R. Castillo, E.G. Ramirez, J. Kacprzyk. – Heidelberg: Springer, 2007. – 855 p.

11.  Passino K.M. Biomimicry of Bacterial Foraging for Distributed Optimization and Control // IEEE Control System Magazine. – 2002. – № 3 (22). – P. 52-67.