Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Обзор исследований и разработок
- 3.1 Обзор международных источников
- 3.2 Обзор локальных источников
- 4. Параллельные итерационные методы решения жестких задач Коши
- Выводы
- Список источников
Введение
Идея распараллеливания вычислений базируется на том, что большинство задач может быть разделено на набор меньших задач, которые могут быть решены одновременно. Обычно параллельные вычисления требуют координации действий. Параллельные вычисления существуют в нескольких формах: параллелизм на уровне битов, параллелизм на уровне инструкций, параллелизм данных, параллелизм задач. Параллельные вычисления использовались много лет в основном в высокопроизводительных вычислениях, но в последнее время к ним возрос интерес вследствие существования физических ограничений на рост тактовой частоты процессоров. Параллельные вычисления стали доминирующей парадигмой в архитектуре компьютеров, в основном в форме многоядерных процессоров [1].
Применение параллельных вычислительных систем является стратегическим направлением развития современной компьютерной индустрии. Это обстоятельство вызвано не столько принципиальным ограничением максимально возможного быстродействия последовательных машин, сколько наличием вычислительных задач, для решения которых возможностей существующих средств вычислительной техники является недостаточным. К таким задачам относится решение систем обыкновенных дифференциальных уравнений большой размерности, используемое при моделировании различных динамических процессов с сосредоточенными параметрами [2].
Появление многоядерных процессоров является качественным скачком на пути создания эффективных супервычислителей, обладающих существенно более высокими показателями производительность/стоимость, по сравнению с существующими высокопроизводительными системами вычислений на базе суперЭВМ (электронные вычислительные машины) и кластерных систем. Многоядерные процессоры в силу своих исключительных вычислительных возможностей являются наиболее перспективными средствами аппаратной поддержки нейросетевых и информационных технологий, связанных с интенсивными вычислениями. Использование многоядерных процессоров предоставляет гибкие возможности в части варьирования конфигураций и масштабирования мощности вычислительных систем, - от персональных компьютеров, рабочих станций, серверов до кластерных систем.
1. Актуальность темы
Появление в последние годы большого количества сравнительно дешевых кластерных параллельных вычисленных систем привело к быстрому развитию параллельных вычислительных технологий, в том числе и в области высокопроизводительных вычислений. В последнее время ситуация в области параллельных вычислительных технологий начала кардинально меняться в связи с тем, что большинство основных производителей микропроцессоров стало переходить на многоядерные архитектуры. Изменение аппаратной базы заставляет менять и подходы к построению параллельных алгоритмов. Для реализации вычислительных возможностей многоядерных архитектур требуется разработка новых параллельных алгоритмов, учитывающих новые технологии. Эффективность использования вычислительных ресурсов, которой будут обладать кластеры нового поколения, напрямую будет зависеть от качества собственно параллельных приложений, так и специализированных библиотек численных алгоритмов, ориентированных на многоядерные архитектуры [3].
Моделирование реальных экономических, технических и других процессов, описываемых системами обыкновенных дифференциальных уравнений (СОДУ) большой размерности, представляет собой обширный класс задач, для решения которых применение высокопроизводительной вычислительной техники не только оправдано, но и необходимо. Один из наиболее эффективных способов повышения производительности заключается в распараллеливании вычислений в многопроцессорных и параллельных структурах. Вследствие чего, применение параллельных вычислительных систем является довольно важным направлением развития вычислительной техники.
2. Цель и задачи исследования, планируемые результаты
Целью исследования является усовершенствование и определение оптимальных параллельных полностью неявных алгоритмов решения жестких задач Коши для систем обыкновенных дифференциальных уравнений для определенного вида вычислительной схемы.
Для достижения цели в магистерской работе решаются следующие основные задачи исследования:
- Изучение существующих методов решения задачи.
- Анализ эффективности применения различных неявных методов.
- Исследование особенностей реализации методов на вычислительных системах различных топологий.
- Усовершенствование существующих алгоритмов и методов с целью повышения эффективности решения задачи.
- Программная реализация системы, позволяющей экспериментально оценить эффективность полученных алгоритмов.
- Разработка тестовых примеров для исследования эффективности реализованных методов.
- Проведение экспериментов и анализ результатов.
Объект исследования: решение жестких задач Коши.
Предмет исследования: неявные методы численного решения жестких задачи Коши, топологии вычислительных систем, используемые для решения задач данного типа.
В рамках магистерской работы планируется получение актуальных научных результатов по следующим направлениям:
- Усовершенствование алгоритмов, реализующих неявные методы численного решения задачи Коши.
- Разработка тестовых задач для оценки эффективности алгоритмов.
- Получение и последующее исследование результатов для выявления зависимостей между скоростью сходимости методов, параметрами системы и выбором опорного метода.
В качестве практических результатов планируется разработка программного комплекса для оценки производительности сетевых процессоров, включающего в себя следующие компоненты:
- Разработка программной системы, реализующей полученные алгоритмы и позволяющей оценить их практическую временную сложность.
- Проведение экспериментов с использованием вычислительных систем SIMD (single instruction, multiple data) и MIMD (multiple instruction, multiple data) архитектур.
3. Обзор исследований и разработок
Решение жестких задач Коши для систем дифференциальных уравнений является важной научной задачей, которая рассматривается несколькими исследовательскими группами во всем мире.
3.1 Обзор международных источников
Швейцарские специалисты Э. Хайрер и Г. Ваннер по численному анализу в [4] обсуждают одно- и многошаговые, явные и неявные методы. Рассматривают жёсткие и алгебро-дифференциальные уравнения, обсуждают многочисленные способы определения и обеспечения устойчивости и точности численных алгоритмов.
В.П. Гергель и Р.Г. Стронгин из России занимаются исследованиями параллельных неявных методов решения жестких задач Коши. В [5] дается краткая характеристика принципов построения параллельных вычислительных систем, рассматриваются математические модели параллельных алгоритмов и программ для анализа эффективности параллельных вычислений, приводятся примеры конкретных параллельных методов для решения типовых задач вычислительной математики. Ученые предоставляют материалы по кластерным вычислительным системам, анализу трудоемкости коммуникационных операций, параллельным методам решения типовых задач вычислительной математики. В пособие включены результаты вычислительных экспериментов на кластере Нижегородского университета.
Блочные методы для решения обыкновенных дифференциальных уравнений на параллельных ЭВМ описываются P.J. Van der Houwen в труде [6]. Многоблочные методы решения ОДУ обсуждаются M.T. Chu и H. Hamilton в [7], приводятся методы распределения задач на процессорах, а также возможное ускорение. Gear C.W. в работе [8] рассматривает параллельные методы для решения ОДУ.
Различные модификации многошаговых методов численного интегрирования обыкновенных дифференциальных уравнений рассмотрены J.C. Butcher и приведены в [9]. Наконец, Д. Глызин в [10] рассматривает применение класса Рунге-Кутты в параллельных вычислениях с использованием технологии CUDA.
3.2 Обзор локальных источников
Национальные исследования проблем повышения эффективности численного решения многомерных задач Коши проводятся сотрудниками Донецкого национального технического университета.
Профессор Лев Петрович Фельдман и доцент Ирина Акоповна Назарова (ДонНТУ) в [11] рассмотрели параллельный алгоритм решения систем ОДУ, ориентированный на системы с SIMD-архитектурой. Были получены характеристики алгоритма, такие как время выполнения, ускорение и эффективность параллельной реализации.
Уже совместно с профессором Анатолием Ивановичем Петренко (КПИ) и доцентом Ольгой Анатольевной Дмитриевой (ДонНТУ) профессор Лев Петрович Фельдман (ДонНТУ) в [12] подробно осветили современные численные методы решения систем уравнений, в том числе и жестких. Особое внимание уделено практической реализации методов.
В [13] доцентом Татьяной Васильевной Михайловой были предложены модифицированные методы анализа и синтеза высокопроизводительных вычислительных ресурсов различной топологии с помощью вероятностных моделей, позволяющие анализировать и проектировать более широкий класс высокопроизводительных параллельных вычислительных сред.
4. Параллельные итерационные методы решения жестких задач Коши
Параллельные алгоритмы одношаговых методов численного решения задачи Коши, которые могут применяться для решения, как жестких, так и нежестких задач. Рассмотрим их реализацию [14]. Для системы из m обыкновенных дифференциальных уравнений:
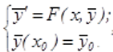
где 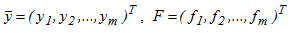 - правая часть есть в общем случае нелинейная функция
- правая часть есть в общем случае нелинейная функция 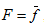 , задающая отображение:
, задающая отображение: 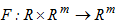 .
.
Одношаговый многостадийный метод для решения нелинейной задачи Коши, описываемой СОДУ, имеет вид:
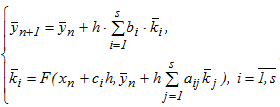
где s-размерные вектора 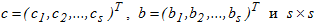 - матрица
- матрица 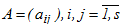 описывают уникальный вариант метода и выбираются из соображений точности. Вид матрицы A задает тип численной схемы, положенной в основу метода. Если ai,j=0 при i≤j, то метод является явным и при наличии малой степени параллелизма, обладает условной устойчивостью. При полностью заполненной матрице имеем полностью неявную схему, применяемую для решения жестких задач.
описывают уникальный вариант метода и выбираются из соображений точности. Вид матрицы A задает тип численной схемы, положенной в основу метода. Если ai,j=0 при i≤j, то метод является явным и при наличии малой степени параллелизма, обладает условной устойчивостью. При полностью заполненной матрице имеем полностью неявную схему, применяемую для решения жестких задач.
Класс неявных численных схем представлен в докладе двумя типами методов: блочные одношаговые методы и полностью неявные методы типа Рунге-Кутты (ПНМРК). К достоинствам полностью неявных, одношаговых методов общего вида (на основе квадратурных формул Радо и Лобатто [15]) следует отнести хорошие характеристики устойчивости и точности, достаточные для решения жестких задач. Недостатками этих методов является высокая вычислительная сложность, обусловленная итерационным процессом определения стадийных коэффициентов, которая не позволяет эффективно применять эти методы на последовательных машинах.
Очевидно, что в отличие от явных методов применение полностью неявных многостадийных методов (ПНММ) требует для определения коэффициентов 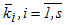 решения системы s x m , в общем случае нелинейных, уравнений:
решения системы s x m , в общем случае нелинейных, уравнений:
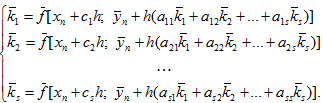
Решение данной системы может быть получено с использованием следующей итерационной схемы:
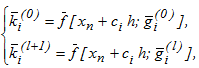
где 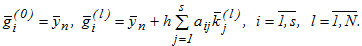
Здесь итерационный процесс, повторенный l-раз представляет 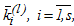 , как l-тую аппроксимацию для шагового коэффициента
, как l-тую аппроксимацию для шагового коэффициента 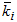 .
.
Скорость сходимости итерационного процесса может быть определена следующим образом: 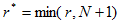 , где r-порядок используемого ПНММ.
, где r-порядок используемого ПНММ.
Блочные или многоточечные неявные методы решения задачи Коши особенно актуальны, поскольку хорошо согласуются с архитектурой параллельных ВС и не требуют вычисления значений в промежуточных точках, что значительно повышает эффективность счета. Данные методы обладают высокой устойчивостью и, что наиболее существенно, являются изначально параллельными, так как позволяют получать решение одновременно в нескольких точках сетки интегрирования.
Множество точек равномерной сетки 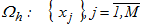 разбивается на N блоков, каждый из которых содержит k точек.
разбивается на N блоков, каждый из которых содержит k точек.
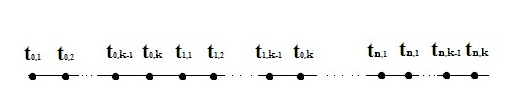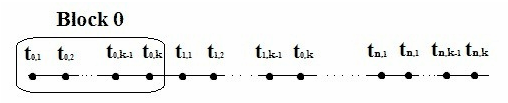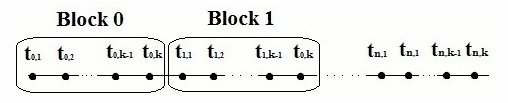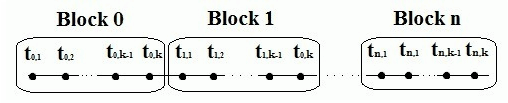
Уравнения одношаговых блочных разностных методов в применении к ОДУ для блока из k точек может быть записано в виде:
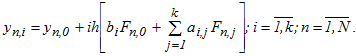
Разложением в ряд Тейлора входящих в невязку функций можно показать, что одношаговый k-точечный блочный метод имеет наивысший порядок аппроксимации равный k+1, следовательно, локальная ошибка в узлах блока имеет порядок 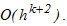 . Блочные параллельные методы относятся к классу неявных, поэтому для вычисления приближенных значений решения задачи Коши необходимо разрешить систему нелинейных уравнений.
. Блочные параллельные методы относятся к классу неявных, поэтому для вычисления приближенных значений решения задачи Коши необходимо разрешить систему нелинейных уравнений.
Одним из способов получения решения является метод простой функциональной итерации:
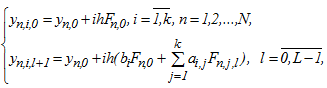
где 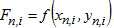 , n - номер блока, n = 1,2,…,N;
, n - номер блока, n = 1,2,…,N;
i - номер точки блока, 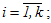 ;
;
l - номер текущей итерации 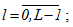 ;
;
L - максимальное число ненулевых итераций.
В отличие от явных методов решения СОДУ, реализация альтернативных способов оценки апостериорной локальной погрешности на основе блочных методов связана с рядом особенностей:
- нет соответствующих последовательных аналогов, следовательно, требуется разработать и обосновать метод оценки локальной погрешности;
- варьировать шаг интегрирования возможно только после вычисления всех значений в k узлах текущего n-го блока;
- при условии неудовлетворительной оценки локальной погрешности и необходимости изменения шага интегрирования практически все вычисления для точек блока окажутся напрасными (некоторые обращения к правой части могут быть использованы вновь).
Для минимизации вычислительные затраты и достижения некоторой заданной точности приближенного решения, численный алгоритм должен иметь механизм управления шагом интегрирования. Это возможно на основе информации об апостериорной локальной погрешности. Для реализации поставленной цели использовались альтернативные способы оценки погрешности на шаге:
- дублирование шага по правилу Рунге;
- вложенные пары схем;
- технология локальной экстраполяции Ричардсона [15].
Проведем сравнение двух классов неявных методов при последовательной и параллельной реализациях на основе наиболее эффективного способа оценки локальной погрешности, а, именно, вложенных формул. Основными параметрами, характеризующими ПНМРК, являются: порядок метода r и число стадий s, причем эти величины являются взаимосвязанными. Кроме того, при решении систем нелинейных алгебраических уравнений для определения стадийных коэффициентов появляется такой параметр, как необходимое число итераций: L. Соответственно, вычислительная сложность блочных методов зависит от порядка метода r, числа точек в блоке k и также числа итераций для получения решения СНАУ необходимой точности: 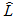 . Для того, чтобы сравнение численных методов на базе неявных одношаговых схем было корректным, необходимо:
. Для того, чтобы сравнение численных методов на базе неявных одношаговых схем было корректным, необходимо:
- обеспечить один и тот же порядок точности, r;
- получить решение в одинаковом числе новых точек, k;
- порождаемые итерационные процессы должны реализовывать предельное число итераций, предусмотренное каждым из рассматриваемых методов: L=2s и
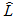 =k.
=k.
Для широко применяемых ПНМРК по теоремам Батчера число стадий связано с порядком метода одним из следующих соотношений: метод Гаусса r=2s; методы Радо r=2s-1; методы Лобатто r=2s-2. Возьмем соотношение r=2s, тем самым намеренно выбирая лучший вариант для ПНМРК. В то же время для блочных одношаговых методов порядок может быть определен через число точек одного блока: r=k+1. Тогда, число стадий ПНМРК и число точек в блоке многоточечного метода связаны следующим соотношением: r=2s=k+1 ⇒ k=2s-1. Используя полученные соотношения, приведем все временные характеристики к одному параметру, пусть это будет число стадий s. Заметим, что среди множества неявных методов типа Рунге-Кутты для сравнения выбраны именно полностью неявные методы, поскольку они обладают идентичными характеристиками устойчивости, что и блочные одношаговые методы, а также в силу оптимального соотношения между порядком и числом стадий методов [16].
Сравним времена выполнения последовательных алгоритмов рассматриваемых методов. При доминировании в вычислениях времени обращения к правой части ОДУ объем вычислений для ПНМРК в s раз больше, чем для блочных методов, аналогично, для параллельного выполнения алгоритмов имеем - в 2s раз [17].
Для тривиальной правой части получается аналогичный результат, последовательная и параллельная реализации вычисления решения в новых k точках сетки интегрирования требуют больших накладных расходов для неявных методов Рунге-Кутты по сравнению с блочными методами. Заметим, что для параллельных алгоритмов эта разница увеличивается почти в 2 раза, что подтверждается проведенным экспериментом на тестовых задачах.
Оценка эффективности распараллеливания производится на основе показателей ускорения вычислений (рис. 1-2) по сравнению со своим последовательным алгоритмом (абсолютный коэффициент ускорения) и по сравнению с наилучшим из рассмотренных последовательных алгоритмов (относительный коэффициент ускорения).
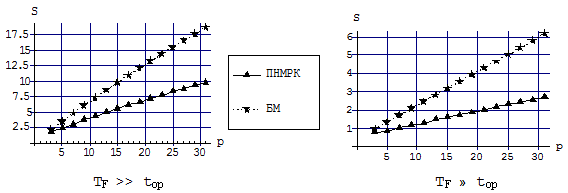
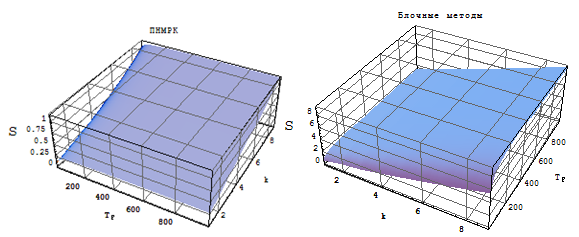
На основе аналогичных исследований можно сделать вывод, что для любых способов оценки локальной погрешности блочные многоточечные одношаговые методы являются наиболее эффективными с точки зрения вычислительных затрат по сравнению с полностью неявными методами Рунге-Кутты.
Выводы
Повышение эффективности численного высокоточного решения задач Коши для систем уравнений является актуальной научной задачей.
Магистерская работа посвящена решению жестких задач Коши для систем обыкновенных дифференциальных уравнений. В рамках проведенных исследований выполнено:
- Проанализированы полностью неявные методы типа Рунге-Кутты и блочные методы решения жестких задач Коши.
- Выполнено сравнение методов и теоретических характеристик.
- Программно реализована аналитическая модель решения СОДУ полностью неявными методами типа Рунге-Кутты.
- Получены и исследованы зависимости показателей эффективности архитектуры от интенсивности порядка метода и количества процессоров.
Дальнейшие исследования направлены на следующие аспекты:
- Реализация полностью неявных методов с помощью технологии CUDA.
- Разработка параллельной версии вычислительных модулей.
- Проведение экспериментов и анализ эффективности методов в зависимости от архитектуры.
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2013 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Операционные системы современных вычислительных комплексов [Электронный ресурс]. Режим доступа:
http://works.doklad.ru/view/t_Nad-J_iTQ.html
- Никишин Р.Ю., Назарова И. А.,Фельдман Л.П. Кластерная реализация параллельных итерационных методов решения жестких задач Коши / Р.Ю. Никишин, И.А. Назарова, Л.П. Фельдман // Материалы IV международной научно-техническая конференции студентов, аспирантов и молодых ученых «Информационные управляющие системы и компьютерный мониторинг – 2013». – Донецк, 2013. – Т. 2. – С. 235-241.
- Дмитриева O.А. Анализ параллельных алгоритмов численного решения систем обыкновенных дифференциальных уравнений методами Адамса-Башфорта и Адамса-Моултона / O.А. Дмитриева // Материалы X международной конференции по вычислительной механике и современным прикладным программным системам. – Переславль-Залесский, 2008. – Т.12. – С. 81-86.
- Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. – М.: Мир,1999. – 685с.
- Гергель В.П., Стронгин Р.Г. Основы параллельных вычислений для многопроцессорных вычислительных систем. Учебное пособие. Издательство Нижегородского госуниверситета, Нижний Новгород, 2003.
- Van der Houwen P.J. Block Runge-Kutta Methods / Van der Houwen P.J. // Centrum voor Wiskunde en Informatica. – 1989. – p. 3-18.
- Chu M.T., Hamilton H. Parallel Solution of ODE’s by Multiblock Methods / Chu M.T., Hamilton H. // Journal on Scientific and Statistical Computing. – 1987. – vol. 8. – pp. 342-353.
- Gear C.W. Parallel methods for ordinary differential equations / Gear C.W. // Journal CALCOLO. – 1988. – vol. 25. – pp. 1-20.
- Butcher J.C. A Modified Multistep Method for the Numerical Integration of Ordinary Differential Equations / Butcher J.C. // Journal of the ACM (JACM). – 1965. - vol. 12 – pp. 124-136.
- Массивный параллелизм и синхронизация в CUDA на примере решения системы ОДУ большой размерности [Электронный ресурс]. Режим доступа: http://parallel.ncycle.org/cuda_sync.pdf
- Фельдман Л.П., Назарова И.А. Применение технологии локальной экстраполяции для высокоточного решения задачи Коши на SIMD-структурах // Научные труды Донецкого национального технического университета. Выпуск 70. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ-2003) – Донецк: ДонНТУ, 2003.
- Чисельні методи в інформатиці : підручник для вузів / Лев Петрович Фельдман, Анатолій Іванович Петренко, Ольга Анатоліївна Дмитрієва ; За заг. ред. М.З. Згуровський . – Київ : BHV, 2006 . – 479 с.
- Михайлова Т.В. Оценка эффективности высокопроизводительных вычислительных систем с использованием аналитических методов// Материалы 2-й международной научно-технической конференции " Моделирование и компьютерная графика", г. Донецк, 10-12 октября 2007 г.
- Хайрер Э., Нёрсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи: Пер. с англ. – М.: Мир, 1990. – 512с.
- Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. – М.: Мир,1999. – 685с.
- Никишин Р.Ю., Назарова И. А.,Фельдман Л.П. Параллельные неявыные методы решения жестких задач Коши для систем обыкновенных дифференциальных уравнений/ Р.Ю. Никишин, И.А. Назарова, Л.П. Фельдман // Материалы VIII международной научно-техническая конференции студентов, аспирантов и молодых ученых «Информатика и компьютерные технологии – 2012». – Донецк, 2012. – Т. 2. – С. 91-95.
- Фельдман Л.П., Назарова И.А. Эффективность параллельных алгоритмов оценки локальной апостериорной погрешности для численного решения задачи Коши // Электронное моделирование, т. 29, № 3, 2007. – С. 11-25.
