Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і задачі дослідження та заплановані результати
- 3. Огляд досліджень та розробок
- 3.1 Огляд міжнародних джерел
- 3.2 Огляд локальних джерел
- 4. Паралельні ітераційні методи розв'язання жорстких задач Коші
- Висновки
- Перелік посилань
Вступ
Ідея розпаралелювання обчислень базується на тому, що більшість завдань може бути розділене на набір менших завдань, які можуть бути вирішені одночасно. Зазвичай паралельні обчислення вимагають координації дій. Паралельні обчислення існують в декількох формах: паралелізм на рівні бітів, паралелізм на рівні інструкцій, паралелізм даних, паралелізм завдань. Паралельні обчислення використовувалися багато років в основному у високопродуктивних обчисленнях, але останнім часом до них зріс інтерес внаслідок існування фізичних обмежень на зростання тактової частоти процесорів. Паралельні обчислення стали домінуючою парадигмою в архітектурі комп'ютерів, в основному у формі багатоядерних процесорів [1].
Застосування паралельних обчислювальних систем є стратегічним напрямком розвитку сучасної комп'ютерної індустрії. Ця обставина викликано не стільки принциповим обмеженням максимально можливого швидкодії послідовних машин, скільки наявністю обчислювальних завдань, для вирішення яких можливостей існуючих засобів обчислювальної техніки є недостатнім. До таких завдань належить вирішення систем звичайних диференціальних рівнянь великої розмірності, що використовується при моделюванні різних динамічних процесів з зосередженими параметрами [2].
Поява багатоядерних процесорів є якісним стрибком на шляху створення ефективних супервичіслітелей, що володіють істотно більш високими показниками продуктивність/вартість, в порівнянні з існуючими високопродуктивними системами обчислень на базі суперЕОМ (електронні обчислювальні машини) і кластерних систем. Багатоядерні процесори в силу своїх виняткових обчислювальних можливостей є найбільш перспективними засобами апаратної підтримки нейромережевих та інформаційних технологій, пов'язаних з інтенсивними обчисленнями. Використання багатоядерних процесорів надає гнучкі можливості в частині варіювання конфігурацій і масштабування потужності обчислювальних систем, - від персональних комп'ютерів, робочих станцій, серверів до кластерних систем.
1. Актуальність теми
Поява в останні роки великої кількості порівняно дешевих кластерних паралельних обчислених систем призвело до швидкого розвитку паралельних обчислювальних технологій, у тому числі і в області високопродуктивних обчислень. Останнім часом ситуація в області паралельних обчислювальних технологій почала кардинально змінюватися у зв'язку з тим, що більшість основних виробників мікропроцесорів стало переходити на багатоядерні архітектури. Зміна апаратної бази змушує змінювати і підходи до побудови паралельних алгоритмів. Для реалізації обчислювальних можливостей багатоядерних архітектур потрібна розробка нових паралельних алгоритмів, які враховують нові технології. Ефективність використання обчислювальних ресурсів, якій будуть володіти кластери нового покоління, безпосередньо залежатиме від якості власне паралельних додатків, так і спеціалізованих бібліотек чисельних алгоритмів, орієнтованих на багатоядерні архітектури [3].
Моделювання реальних економічних, технічних та інших процесів, що описуються системами звичайних диференціальних рівнянь (СЗДР) великої розмірності, являє собою великий клас задач, для вирішення яких застосування високопродуктивної обчислювальної техніки не тільки виправдано, але й необхідно. Один з найбільш ефективних способів підвищення продуктивності полягає в розпаралелюванні обчислень в багатопроцесорних і паралельних структурах. Внаслідок чого, застосування паралельних обчислювальних систем є досить важливим напрямком розвитку обчислювальної техніки.
2. Мета і задачі дослідження та заплановані результати
Метою дослідження є удосконалення та визначення оптимальних паралельних повністю неявних алгоритмів розв'язання жорстких задач Коші для систем звичайних диференціальних рівнянь для певного виду обчислювальної схеми.
Для досягнення мети в магістерській роботі вирішуються такі основні завдання дослідження:
- Вивчення існуючих методів рішення задачі.
- Аналіз ефективності застосування різних неявних методів.
- Дослідження особливостей реалізації методів на обчислювальних системах різних топологій.
- Удосконалення існуючих алгоритмів і методів з метою підвищення ефективності вирішення завдання.
- Програмна реалізація системи, що дозволяє експериментально оцінити ефективність отриманих алгоритмів.
- Розробка тестових прикладів для дослідження ефективності реалізованих методів.
- Проведення експериментів та аналіз результатів.
Об'єкт дослідження: розв'язання жорстких задач Коші.
Предмет дослідження: неявні методи чисельного розв'язання жорстких задачі Коші, топології обчислювальних систем, що використовуються для вирішення завдань даного типу.
В рамках магістерської роботи планується отримання актуальних наукових результатів по наступним напрямкам:
- Удосконалення алгоритмів, що реалізують неявні методи чисельного розв'язання задачі Коші.
- Розробка тестових завдань для оцінки ефективності алгоритмів.
- Отримання і подальше дослідження результатів для виявлення залежностей між швидкістю збіжності методів, параметрами системи і вибором опорного методу.
В якості практичних результатів планується розробка програмного комплексу для оцінки ефективності мережевих процесорів, що включає в себе наступні компоненти:
- Розробка програмної системи, що реалізує отримані алгоритми і дозволяє оцінити їх практичну тимчасову складність.
- Проведення експериментів з використанням обчислювальних систем SIMD (single instruction, multiple data) і MIMD (multiple instruction, multiple data) архітектур.
3. Огляд досліджень та розробок
Рішення жорстких задач Коші для систем диференціальних рівнянь є важливою науковою задачею, яка розглядається кількома дослідницькими групами в усьому світі.
3.1 Огляд міжнародних джерел
Швейцарські фахівці Е. Хайрер і Г. Ваннер за чисельним аналізу в [4] обговорюють одно-і багатокрокові, явні і неявні методи. Розглядають жорсткі і алгебро-диференціальні рівняння, обговорюють численні способи визначення та забезпечення стійкості і точності чисельних алгоритмів.
В.П. Гергель і Р.Г. Стронгин з Росії займаються дослідженнями паралельних неявних методів розв'язання жорстких задач Коші. В [5] дається коротка характеристика принципів побудови паралельних обчислювальних систем, розглядаються математичні моделі паралельних алгоритмів і програм для аналізу ефективності паралельних обчислень, наводяться приклади конкретних паралельних методів для вирішення типових задач обчислювальної математики. Вчені надають матеріали по кластерним обчислювальним системам, аналізу трудомісткості комунікаційних операцій, паралельним методам вирішення типових задач обчислювальної математики. У посібник включені результати обчислювальних експериментів на кластері Нижегородського університету.
Блокові методи для вирішення звичайних диференціальних рівнянь на паралельних ЕОМ описуються P.J. Van der Houwen у праці [6]. Багатоблокові методи вирішення ОДУ обговорюються M.T. Chu і H. Hamilton в [7], наводяться методи розподілу завдань на процесорах, а також можливе прискорення. Gear C.W. в роботі [8] розглядає паралельні методи для вирішення ОДУ.
Різні модифікації багатокрокових методів чисельного інтегрування звичайних диференціальних рівнянь розглянуті J.C. Butcher та приведені в [9]. Нарешті, Д. Глизін в [10] розглядає застосування класу Рунге-Кутта в паралельних обчисленнях з використанням технології CUDA.
3.2 Огляд локальних джерел
Національні дослідження проблем підвищення ефективності чисельного рішення багатовимірних задач Коші проводяться співробітниками Донецького національного технічного університету.
Професор Лев Петрович Фельдман і доцент Ірина Акопівна Назарова (ДонНТУ) в [11] розглянули паралельний алгоритм розв'язання систем ОДУ, орієнтований на системи з SIMD-архітектурою. Були отримані характеристики алгоритму, такі як час виконання, прискорення і ефективність паралельної реалізації.
Вже спільно з професором Анатолієм Івановичем Петренко (КПІ) та доцентом Ольгою Анатоліївною Дмитрієвої (ДонНТУ) професор Лев Петрович Фельдман (ДонНТУ) в [12] детально висвітлили сучасні чисельні методи розв'язання систем рівнянь, у тому числі і жорстких. Особливу увагу приділено практичній реалізації методів.
В [13] доцентом Тетяною Василівною Михайлової були запропоновані модифіковані методи аналізу та синтезу високопродуктивних обчислювальних ресурсів різної топології за допомогою імовірнісних моделей, що дозволяють аналізувати і проектувати більш широкий клас високопродуктивних паралельних обчислювальних середовищ.
4. Паралельні ітераційні методи розв'язання жорстких задач Коші
Паралельні алгоритми однокрокових методів чисельного рішення задачі Коші, які можуть застосовуватися для вирішення, як жорстких, так і нежорстких завдань. Розглянемо їх реалізацію [14]. Для системи з m звичайних диференціальних рівнянь:
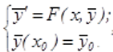
де 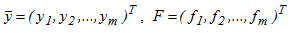 - права частина є в загальному випадку нелінійна функція
- права частина є в загальному випадку нелінійна функція 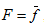 , що задає відображення:
, що задає відображення: 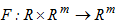 .
.
Однокроковий багатостадійний метод для вирішення нелінійної задачі Коші, описуваної СЗДР, має вигляд:
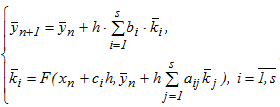
де s-розмірні вектора 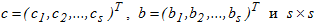 - матриця
- матриця 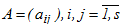 описують унікальний варіант методу і вибираються з міркувань точності. Вид матриці A задає тип чисельної схеми, покладеної в основу методу. Якщо i,j=0 при i≤j, то метод є явним і за наявності малою мірою паралелізму, володіє умовною стійкістю. При повністю заповненої матриці маємо повністю неявну схему, застосовувану для вирішення жорстких задач.
описують унікальний варіант методу і вибираються з міркувань точності. Вид матриці A задає тип чисельної схеми, покладеної в основу методу. Якщо i,j=0 при i≤j, то метод є явним і за наявності малою мірою паралелізму, володіє умовною стійкістю. При повністю заповненої матриці маємо повністю неявну схему, застосовувану для вирішення жорстких задач.
Клас неявних чисельних схем представлений в доповіді двома типами методів: блокові однокрокові методи і повністю неявні методи типу Рунге-Кутта (ПНМРК). До достоїнств повністю неявних, однокрокових методів загального виду (на основі квадратурних формул Радо і Лобатто [15]) слід віднести хороші характеристики стійкості і точності, достатні для вирішення жорстких задач. Недоліками цих методів є висока обчислювальна складність, обумовлена ітераційним процесом визначення стадійних коефіцієнтів, яка не дозволяє ефективно застосовувати ці методи на послідовних машинах.
Очевидно, що на відміну від явних методів застосування повністю неявних багатостадійних методів (ПНММ) вимагає для визначення коефіцієнтів 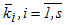 рішення системи s x m, в загальному випадку нелінійних, рівнянь:
рішення системи s x m, в загальному випадку нелінійних, рівнянь:
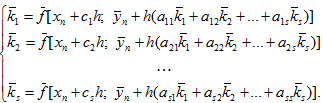
Розв'язання даної системи може бути отримано з використанням наступної ітераційної схеми:
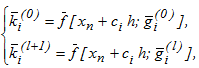
де 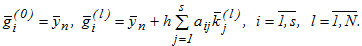
Тут ітераційний процес, повторений l-раз представляє  , як l-ту апроксимацію для крокової коефіцієнта
, як l-ту апроксимацію для крокової коефіцієнта 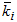 .
.
Швидкість збіжності ітераційного процесу може бути визначена таким чином: 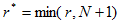 , де r-порядок використовуваного ПНММ.
, де r-порядок використовуваного ПНММ.
Блокові або багатокрапкові неявні методи розв'язання задачі Коші особливо актуальні, оскільки добре узгоджуються з архітектурою паралельних НД і не вимагають обчислення значень в проміжних точках, що значно підвищує ефективність розрахунків. Дані методи мають високу стійкість і, що найбільш суттєво, є спочатку паралельними, оскільки дозволяють отримувати рішення одночасно в декількох точках сітки інтегрування.
Множина точок рівномірної сітки 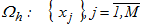 розбивається на N блоків, кожен з яких містить k точок.
розбивається на N блоків, кожен з яких містить k точок.
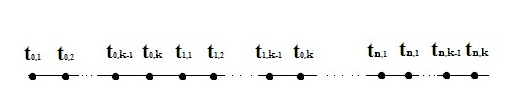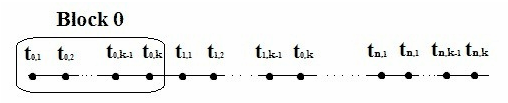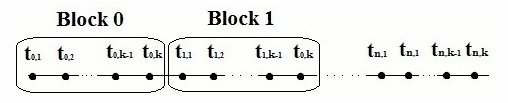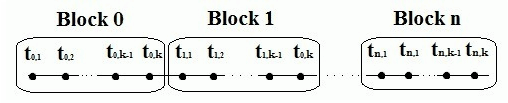
Рівняння однокрокових блокових різницевих методів у застосуванні до ОДУ для блоку з k точок може бути записано у вигляді:
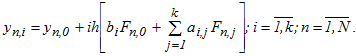
Розкладанням в ряд Тейлора функцій, що входять до нев'язки можна показати, що однокроковий k-точковий блоковий метод має найвищий порядок апроксимації рівний k +1, отже, локальна помилка у вузлах блоку має порядок 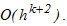 . Блокові паралельні методи відносяться до класу неявних, тому для обчислення наближених значень рішення задачі Коші необхідно дозволити систему нелінійних рівнянь.
. Блокові паралельні методи відносяться до класу неявних, тому для обчислення наближених значень рішення задачі Коші необхідно дозволити систему нелінійних рівнянь.
Одним із способів отримання рішення є метод простий функціональної ітерації:
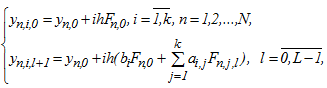
де 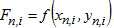 , n - номер блоку, n = 1,2,…,N;
, n - номер блоку, n = 1,2,…,N;
i - номер точки блоку, 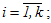 ;
;
l - номер поточної ітерації 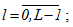 ;
;
L - максимальне число ненульових ітерацій.
На відміну від явних методів вирішення СЗДР, реалізація альтернативних способів оцінки апостеріорної локальної похибки на основі блокових методів пов'язана з низкою особливостей:
- немає відповідних послідовних аналогів, отже, потрібно розробити і обгрунтувати метод оцінки локальної похибки;
- варіювати крок інтегрування можливе тільки після обчислення всіх значень у k вузлах поточного n-го блоку;
- за умови незадовільної оцінки локальної похибки і необхідності зміни кроку інтегрування практично всі обчислення для точок блоку виявляться марними (деякі звернення до правої частини можуть бути використані знову).
Для мінімізації обчислювальні витрати та досягнення деякої заданої точності наближеного рішення, чисельний алгоритм повинен мати механізм управління кроком інтегрування. Це можливо на основі інформації про апостеріорної локальної похибки. Для реалізації поставленої мети використовувалися альтернативні способи оцінки похибки на кроці:
- дублювання кроку за правилом Рунге;
- вкладені пари схем;
- технологія локальної екстраполяції Річардсона [15].
Проведемо порівняння двох класів неявних методів при послідовній і паралельної реалізаціях на основі найбільш ефективного способу оцінки локальної похибки, а, саме, вкладених формул. Основними параметрами, що характеризують ПНМРК, є: порядок методу r і число стадій s, причому ці величини є взаємопов'язаними. Крім того, при вирішенні систем нелінійних алгебраїчних рівнянь для визначення стадійних коефіцієнтів з'являється такий параметр, як необхідна кількість ітерацій: L. Відповідно, обчислювальна складність блокових методів залежить від порядку методу r, числа точок в блоці k і навіть числа ітерацій для отримання рішення СНАУ необхідної точності: 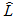 . Для того, щоб порівняння чисельних методів на базі неявних однокрокових схем було коректним, необхідно:
. Для того, щоб порівняння чисельних методів на базі неявних однокрокових схем було коректним, необхідно:
- забезпечити один і той же порядок точності, r;
- отримати рішення в однаковому числі нових точок, k;
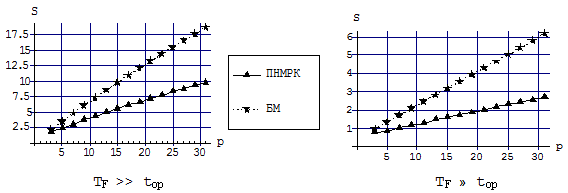
- породжувані ітераційні процеси повинні реалізовувати граничне число ітерацій, передбачене кожним з розглянутих методів: L=2s и
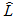 =k.
=k.
Для широко застосовуваних ПНМРК по теоремам Батчера число стадій пов'язано з порядком методу одним з наступних співвідношень: метод Гаусса r = 2s; методи Радо r = 2s-1; методи Лобатто r = 2s-2. Візьмемо співвідношення r = 2s, тим самим навмисно вибираючи кращий варіант для ПНМРК. У той же час для блокових однокрокових методів порядок може бути визначений через число точок одного блоку: r = k +1. Тоді, число стадій ПНМРК і число точок у блоці багатокрапкового методу пов'язані наступним співвідношенням: r = 2s = k +1 ? k = 2s-1. Використовуючи отримані співвідношення, наведемо всі тимчасові характеристики до одного параметру, нехай це буде число стадій s. Зауважимо, що серед безлічі неявних методів типу Рунге-Кутта для порівняння обрані саме повністю неявні методи, оскільки вони мають ідентичними характеристиками стійкості, що і блокові однокрокові методи, а також в силу оптимального співвідношення між порядком і числом стадій методів [16].
Порівняємо часи виконання послідовних алгоритмів розглянутих методів. При домінуванні в обчисленнях часу звернення до правої частини ОДУ обсяг обчислень для ПНМРК в s разів більше, ніж для блокових методів, аналогічно, для паралельного виконання алгоритмів маємо - в 2s разів [17].
Для тривіальної правої частини виходить аналогічний результат, послідовна і паралельна реалізації обчислення рішення в нових k точках сітки інтегрування вимагають великих накладних витрат для неявних методів Рунге-Кутта в порівнянні з блочними методами. Зауважимо, що для паралельних алгоритмів ця різниця збільшується майже в 2 рази, що підтверджується проведеним експериментом на тестових завданнях.
Оцінка ефективності розпаралелювання виробляється на основі показників прискорення обчислень (рис. 1-2) у порівнянні зі своїм послідовним алгоритмом (абсолютний коефіцієнт прискорення) і в порівнянні з найкращим з розглянутих послідовних алгоритмів (відносний коефіцієнт прискорення).
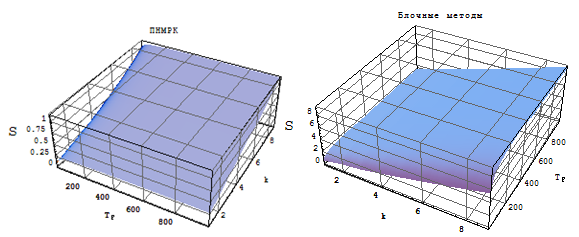
На основі аналогічних досліджень можна зробити висновок, що для будь-яких способів оцінки локальної похибки блокові багатокрапкові однокрокові методи є найбільш ефективними з точки зору обчислювальних витрат в порівнянні з повністю неявними методами Рунге-Кутта.
Висновки
Підвищення ефективності чисельного високоточного вирішення завдань Коші для систем рівнянь є актуальною науковою задачею.
Магістерська робота присвячена вирішенню жорстких задач Коші для систем звичайних диференціальних рівнянь. У рамках проведених досліджень виконано:
- Проаналізовано повністю неявні методи типу Рунге-Кутта і блокові методи розв'язання жорстких задач Коші.
- Виконано порівняння методів і теоретичних характеристик.
- Програмно реалізована аналітична модель вирішення СЗДР повністю неявними методами типу Рунге-Кутта.
- Отримано і досліджено залежності показників ефективності архітектури від інтенсивності порядку методу і кількості процесорів.
Подальші дослідження спрямовані на наступні аспекти:
- Реалізація повністю неявних методів за допомогою технології CUDA.
- Розробка паралельної версії обчислювальних модулів.
- Проведення експериментів і аналіз ефективності методів залежно від архітектури.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2013 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Перелік посилань
- Операційні системи сучасних обчислювальних комплексів [Електронний ресурс]. Режим доступу:
http://works.doklad.ru/view/t_Nad-J_iTQ.html
- Нікішин Р.Ю., Назарова І. А., Фельдман Л.П. Кластерна реалізація паралельних ітераційних методів розв'язання жорстких задач Коші / Р.Ю. Нікішин, І.А. Назарова, Л.П. Фельдман // Матеріали IV міжнародної науково-технічна конференції студентів, аспірантів та молодих вчених "Інформаційні управляючі системи та комп'ютерний моніторинг - 2013". - Донецьк, 2013. - Т. 2. - С. 235-241.
- Дмитрієва O.А. Аналіз паралельних алгоритмів чисельного рішення систем звичайних диференціальних рівнянь методами Адамса-Башфорта і Адамса-Моултона / O.А. Дмитрієва // Матеріали X міжнародної конференції з обчислювальної механіки і сучасним прикладним програмним системам. - Переславль-Залеський, 2008. - Т.12. - С. 81-86.
- Хайрер Е., Ваннер Г. Рішення звичайних диференціальних рівнянь. Жорсткі і диференційно-алгебраїчні завдання. - М.: Мир, 1999. - 685с.
- Гергель В.П., Стронгин Р.Г. Основи паралельних обчислень для багатопроцесорних обчислювальних систем. Навчальний посібник. Видавництво Нижегородського держуніверситету, Нижній Новгород, 2003.
- Van der Houwen P.J. Block Runge-Kutta Methods / Van der Houwen P.J. // Centrum voor Wiskunde en Informatica. – 1989. – p. 3-18.
- Chu M.T., Hamilton H. Parallel Solution of ODE’s by Multiblock Methods / Chu M.T., Hamilton H. // Journal on Scientific and Statistical Computing. – 1987. – vol. 8. – pp. 342-353.
- Gear C.W. Parallel methods for ordinary differential equations / Gear C.W. // Journal CALCOLO. – 1988. – vol. 25. – pp. 1-20.
- Butcher J.C. A Modified Multistep Method for the Numerical Integration of Ordinary Differential Equations / Butcher J.C. // Journal of the ACM (JACM). – 1965. - vol. 12 – pp. 124-136.
- Масивний паралелізм та синхронізація в CUDA на прикладі вирішення системи ОДУ великої розмірності [Електронний ресурс]. Режим доступу: http://parallel.ncycle.org/cuda_sync.pdf
- Фельдман Л.П., Назарова І.А. Застосування технології локальної екстраполяції для високоточного розв'язання задачі Коші на SIMD-структурах // Наукові праці Донецького національного технічного університету. Випуск 70. Серія: "Інформатика, кібернетика та обчислювальна техніка" (ІКВТ-2003) - Донецьк: ДонНТУ, 2003.
- Чисельні методи в інформатиці : підручник для вузів / Лев Петрович Фельдман, Анатолій Іванович Петренко, Ольга Анатоліївна Дмитрієва ; За заг. ред. М.З. Згуровський . – Київ : BHV, 2006 . – 479 с.
- Михайлова Т.В. Оцінка ефективності високопродуктивних обчислювальних систем з використанням аналітичних методів // Матеріали 2-ї міжнародної науково-технічної конференції "Моделювання і комп'ютерна графіка", м. Донецьк, 10-12 жовтня 2007
- Хайрер Е., Нерсетт С., Ваннер Г. Рішення звичайних диференціальних рівнянь. Нежорсткі завдання: Пер. з англ. - М.: Мир, 1990. - 512с.
- Хайрер Е., Ваннер Г. Рішення звичайних диференціальних рівнянь. Жорсткі і диференційно-алгебраїчні завдання. - М.: Мир, 1999. - 685с.
- Нікішин Р.Ю., Назарова І. А., Фельдман Л.П. Паралельні неявиние методи розв'язання жорстких задач Коші для систем звичайних диференціальних рівнянь / Р.Ю. Нікішин, І.А. Назарова, Л.П. Фельдман / / Матеріали VIII міжнародної науково-технічна конференції студентів, аспірантів та молодих вчених "Інформатика та комп'ютерні технології - 2012". - Донецьк, 2012. - Т. 2. - С. 91-95.
- Фельдман Л.П., Назарова І.А. Ефективність паралельних алгоритмів оцінки локальної апостеріорної похибки для чисельного розв'язання задачі Коші / / Електронне моделювання, т. 29, № 3, 2007. - С. 11-25.
