Abstract
Content
- Introduction
- 1. Theme urgency
- 2. Goal and tasks of the research
- Overview of Research and Development
- 3. Parallel iterative methods for solving stiff Cauchy problems
- Conclusion
- References
Introduction
The idea of parallel computing is based on the fact that most of the tasks can be divided into a set of smaller tasks that can be solved simultaneously. Usually parallel computations require coordination. Parallel computing exist in the several forms: parallelism on the level of bits, the concurrency at the level of instructions, concurrency of the data, the concurrency of tasks. Parallel computing used for many years, mainly in high-performance computing, but in recent years has intensified interest due to the existence of the physical constraints on the growth of the CPU clock. Parallel processing has become the dominant paradigm in computer architecture, mainly in the form of multi-processor [1].
The use of parallel computing systems is a strategic direction in the development of modern computer industry. This fact is due not so much a fundamental limitation of the maximum possible speed sequential machines as the presence of computational tasks for which the capacity of existing computer equipment is insufficient. These tasks include the solution of systems of ordinary differential equations of large dimension that is used in the simulation of various dynamic processes with lumped parameters [2].
The emergence of multi-core processors is a quantum leap in the way of effective supercomputers, have significantly higher rates of productivity/cost, compared to existing high-performance computing systems based supercomputers (electronic computers), and clustered systems. Multi-core processors due to their exceptional computing power are the most promising means of neural network hardware support and information technology related to the computationally intensive. The use of multi-core processors offers flexibility in terms of varying configurations and power scaling of computing systems - from personal computers, workstations, servers to cluster systems.
1. Theme urgency
The emergence in recent years of a large number of relatively cheap cluster of parallel computing systems has led to the rapid development of parallel computing technology, including in the field of high performance computing. Recently, the situation in the field of parallel computing technology began to change dramatically due to the fact that most of the major manufacturers of microprocessors began to take the multi-core architecture. Changing the hardware base makes change and approaches to the construction of parallel algorithms. To implement the computational capabilities of multicore architectures requires the development of new parallel algorithms that take into account new technologies. Efficient use of computing resources, which will have clusters of new generation, will depend directly on the quality of the actual parallel applications, as well as specialized libraries of numerical algorithms, focused on multi-core architecture [3].
Simulation of real of economic, of technical and of other processes, described by systems of ordinary of differential of equations (SODE) large the dimension of, represents a an extensive class of problems for solutions which the application of high-performance computing appliances not only justified, but it and necessary. One of the most effective ways to increase performance is to parallelize computations in multiprocessor and parallel structures. As a result, the use of parallel computing systems is a pretty important aspect of computing.
2. Goal and tasks of the research
The aim of the research is to improve and to determine the optimal parallel fully implicit algorithms for solving stiff Cauchy problems for systems of ordinary differential equations for a certain kind of computer circuitry.
To achieve the goal of the master's thesis focuses on the following key objectives of the study:
- The research of existing methods of solving the problem.
- Analysis of the effectiveness of various implicit methods.
- Investigation of the features of the methods for computing systems of different topologies.
- Improvement of existing algorithms and methods to improve the efficiency of solving the problem.
- Software implementation of a system for the experimentally evaluate the effectiveness of this algorithm.
- Development of test of examples for studies of the effectiveness the realized methods.
- Conducting experiments and analysis of results.
Research object: the solution of stiff Cauchy problem.
Research subject: implicit methods for the numerical solution of stiff Cauchy problem, the topology of computer systems that are used for solving problems of this type.
3. Overview of Research and Development
The solution of the Cauchy problem for rigid systems of differential equations is an important scientific problem, which is regarded by several research groups around the world.
3.1 Overview of international sources
Swiss experts E. Hairer and G. Wanner numerical analysis in [4] discuss single-and multi-step, explicit and implicit methods. Consider stiff and differential algebraic equations, discuss the many ways to define and ensure the accuracy and stability of numerical algorithms.
V.P. Gergel and R.G. Strongin of Russia are engaged in research implicit parallel methods for solving stiff Cauchy problems. In [5] we give a brief description of the principles of parallel computing systems, the mathematical model of parallel algorithms and software for analyzing the efficiency of parallel computing, parallel examples of specific methods for solving typical problems of computational mathematics. Scientists provide materials for cluster computing systems, complexity analysis of communication operations, parallel methods for solving typical problems of computational mathematics. The manual includes the results of computational experiments on a cluster of Nizhny Novgorod University.
Block methods for the solution of ordinary differential equations on parallel computers are described by P.J. Van der Houwen in work [6]. Multi-block methods for solving ordinary differential equations are discussed M.T. Chu and H. Hamilton in [7], presents methods for assigning tasks to processors as well as a possible acceleration. Gear CW in [8] considers the parallel methods for the solution of ordinary differential equations.
Various modifications of the multi-step methods for the numerical integration of ordinary differential equations discussed JC Butcher and are given in [9]. Finally, D. Glyzin in [10] discusses the use of a class of Runge-Kutta methods in parallel computing using the technology of CUDA.
3.2 Overview of local sources
National studies the problems of increasing the efficiency of the numerical solution of problems of Cauchy conducted by officers of the Donetsk National Technical University.
Professor Leo P. Feldman and assistant professor Irina Akopovna Nazarova (DNTU) in [11] considered a parallel algorithm for solving ODE systems-oriented system with SIMD-architecture. Were obtained characteristics of the algorithm, such as run time, speedup and efficiency of parallel implementation.
Already with Professor Anatoly Ivanovich Petrenko (KPI) and Associate Professor Olga Dmitrieva (Donetsk National Technical University), Professor Leo P. Feldman (DNTU) in [12] elaborated on modern numerical methods for solving systems of equations, including hard. Particular attention is paid to the practical implementation of methods.
In [13] Associate Professor Tatyana Vasilevnа Mikhailova proposed modified methods of analysis and synthesis of high performance computing resources of different topologies using probabilistic models that allow you to analyze and design a broader class of high-performance parallel computing environments.
4. Parallel iterative methods for solving stiff Cauchy problems
Parallel algorithms for the one-step methods for the numerical solution of the Cauchy problem, which can be used to deal with, both rigid and non-rigid applications. Consider their implementation [14]. For a system of m ordinary differential equations:
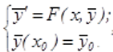
where 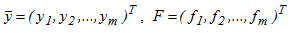 - the right side is generally a nonlinear function
- the right side is generally a nonlinear function 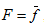 , that defines the mapping:
, that defines the mapping: 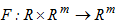 .
.
One-step a multi-step the method of for solutions of the nonlinear problem of Cauchy, described by the SODE, has the form of:
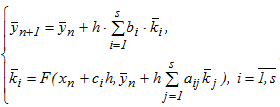
where the s-dimensional vector 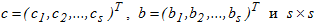 - matrix
- matrix 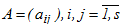 describe a unique variant of the method and are selected for reasons of accuracy. A form of the matrix specifies the type of the numerical scheme, which is the basis of the method. If ai,j=0 when i≤j, then the method is clear and a small degree of parallelism has conditional stability. With a fully-the filled the matrix of we have the fully the implicit scheme that is applied for solutions stiff problems of.
describe a unique variant of the method and are selected for reasons of accuracy. A form of the matrix specifies the type of the numerical scheme, which is the basis of the method. If ai,j=0 when i≤j, then the method is clear and a small degree of parallelism has conditional stability. With a fully-the filled the matrix of we have the fully the implicit scheme that is applied for solutions stiff problems of.
Consider two types of methods: block one-step methods and fully implicit methods of Runge-Kutta (FIMRK).
Conduct a comparison of of two classes of implicit methods of the serial line during and parallel to the implementations,
the on the basis of the most of effective way of an estimation local area error margin as well, namely, the of nested formulas.
The main parameters that characterize FIMRK are: the order of the method r and the number of stages s, and these values are interrelated.
In addition, when solving systems of nonlinear algebraic equations to determine the coefficients of stage there is a parameter such as the
required number of iterations: L. Accordingly, the computational complexity of the block methods depends on the method order r,
the number of points in the block k, and also the number of iterations to obtain the required accuracy SNAU solutions: 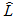 .
In order to compare the numerical methods based on the implicit one-step schemes were correct, it is necessary [15]:
.
In order to compare the numerical methods based on the implicit one-step schemes were correct, it is necessary [15]:
- provide the same order of accuracy, r;
- obtain a solution in the same number of new points, k;
- generated by the iterative processes must implement the maximum number of iterations, provided for each of these methods: L = 2s and
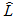 =k.
=k.
For the widely applied by FIMRK, according to Theorems of Batcher the number of stages is connected with order of method by one from the following relations: the method of Gauss r = 2s; methods of Rado's r = 2s-1; methods of Lobatto r = 2s-2. Take the ratio of r = 2s, thereby deliberately choosing the best option for FIMRK. At the same time, one-step methods for block order can be defined by the number of dots per unit: r = k +1. Then, the number of stages and the number of points FIMRK in block multipoint method related as follows: r = 2s = k +1 ⇒ k = 2s-1. Using these relations, we present all the time characteristics of a single parameter, let it be the number of stages s. Note that among the many implicit Runge-Kutta methods chosen for comparison is fully implicit methods, since they have the same characteristics of stability, which block one-step methods, and because of the optimal ratio between the order and the number of stages of the methods [16].
We compare the execution times of sequential algorithms these methods. The dominance in the computation time of the reference to the right of the TAC volume calculations for FNMRK s times larger than for the block methods, similar to the parallel execution of algorithms have - 2s in time [17].
For the trivial right-hand side is obtained a similar result, serial and parallel computing solutions in the implementation of new grid points k integration require a lot of overhead for implicit Runge-Kutta methods in comparison with block methods. Note that for parallel algorithms, this difference increases by almost a factor of 2, which is confirmed by experiment conducted on test problems.
Evaluating the effectiveness of parallelization is based on the speedup of calculations (Fig. 1-2) as compared to its sequential algorithm (absolute acceleration factor) and compared with the best of the considered sequential algorithms (relative rate of acceleration).
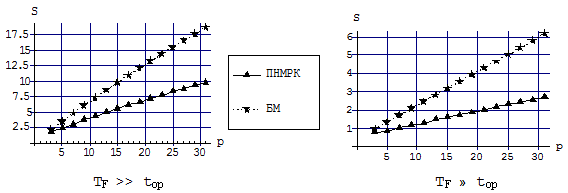
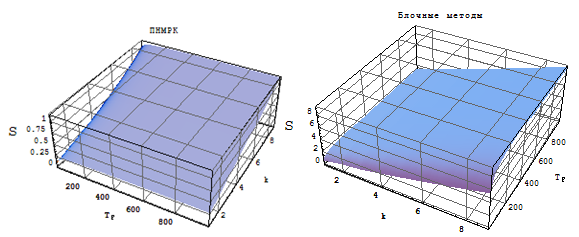
Based on similar studies, we can conclude that for any way to assess the local error block multipoint-step methods are the most efficient in terms of computational cost compared to a fully implicit Runge-Kutta methods.
Conclusion
Improving the efficiency of high-precision numerical solutions of the Cauchy problem for systems of equations is the actual scientific problem.
Master's work is dedicated to the actual scientific problem of network processors architecture modeling. In the trials carried out:
- Analyzed fully implicit methods of Runge-Kutta methods and block methods for solving stiff Cauchy problems.
- A comparison of methods and theoretical characteristics.
- Software-based analytical model solutions SODE fully implicit Runge-Kutta methods.
- Obtained and studied architecture based performance indicators of the intensity of the order of the method and the number of processors.
Further research is focused on the following aspects:
- The implementation of a fully implicit methods with technology CUDA.
- Development of a parallel version of the compute modules.
- Carrying out of experiments and the analysis of efficiency of methods in the depending on the architecture.
This master's work is not completed yet. Final completion: December 2013. The full text of the work and materials on the topic can be obtained from the author or his head after this date.
References
- Операционные системы современных вычислительных комплексов [Электронный ресурс]. Режим доступа:
http://works.doklad.ru/view/t_Nad-J_iTQ.html
- Никишин Р.Ю., Назарова И. А.,Фельдман Л.П. Кластерная реализация параллельных итерационных методов решения жестких задач Коши / Р.Ю. Никишин, И.А. Назарова, Л.П. Фельдман // Материалы IV международной научно-техническая конференции студентов, аспирантов и молодых ученых «Информационные управляющие системы и компьютерный мониторинг – 2013». – Донецк, 2013. – Т. 2. – С. 235-241.
- Дмитриева O.А. Анализ параллельных алгоритмов численного решения систем обыкновенных дифференциальных уравнений методами Адамса-Башфорта и Адамса-Моултона / O.А. Дмитриева // Материалы X международной конференции по вычислительной механике и современным прикладным программным системам. – Переславль-Залесский, 2008. – Т.12. – С. 81-86.
- Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. – М.: Мир,1999. – 685с.
- Гергель В.П., Стронгин Р.Г. Основы параллельных вычислений для многопроцессорных вычислительных систем. Учебное пособие. Издательство Нижегородского госуниверситета, Нижний Новгород, 2003.
- Van der Houwen P.J. Block Runge-Kutta Methods / Van der Houwen P.J. // Centrum voor Wiskunde en Informatica. – 1989. – p. 3-18.
- Chu M.T., Hamilton H. Parallel Solution of ODE’s by Multiblock Methods / Chu M.T., Hamilton H. // Journal on Scientific and Statistical Computing. – 1987. – vol. 8. – pp. 342-353.
- Gear C.W. Parallel methods for ordinary differential equations / Gear C.W. // Journal CALCOLO. – 1988. – vol. 25. – pp. 1-20.
- Butcher J.C. A Modified Multistep Method for the Numerical Integration of Ordinary Differential Equations / Butcher J.C. // Journal of the ACM (JACM). – 1965. - vol. 12 – pp. 124-136.
- Массивный параллелизм и синхронизация в CUDA на примере решения системы ОДУ большой размерности [Электронный ресурс]. Режим доступа: http://parallel.ncycle.org/cuda_sync.pdf
- Фельдман Л.П., Назарова И.А. Применение технологии локальной экстраполяции для высокоточного решения задачи Коши на SIMD-структурах // Научные труды Донецкого национального технического университета. Выпуск 70. Серия: «Информатика, кибернетика и вычислительная техника» (ИКВТ-2003) – Донецк: ДонНТУ, 2003.
- Чисельні методи в інформатиці : підручник для вузів / Лев Петрович Фельдман, Анатолій Іванович Петренко, Ольга Анатоліївна Дмитрієва ; За заг. ред. М.З. Згуровський . – Київ : BHV, 2006 . – 479 с.
- Михайлова Т.В. Оценка эффективности высокопроизводительных вычислительных систем с использованием аналитических методов// Материалы 2-й международной научно-технической конференции " Моделирование и компьютерная графика", г. Донецк, 10-12 октября 2007 г.
- Хайрер Э., Нёрсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи: Пер. с англ. – М.: Мир, 1990. – 512с.
- Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. – М.: Мир,1999. – 685с.
- Никишин Р.Ю., Назарова И. А.,Фельдман Л.П. Параллельные неявыные методы решения жестких задач Коши для систем обыкновенных дифференциальных уравнений/ Р.Ю. Никишин, И.А. Назарова, Л.П. Фельдман // Материалы VIII международной научно-техническая конференции студентов, аспирантов и молодых ученых «Информатика и компьютерные технологии – 2012». – Донецк, 2012. – Т. 2. – С. 91-95.
- Фельдман Л.П., Назарова И.А. Эффективность параллельных алгоритмов оценки локальной апостериорной погрешности для численного решения задачи Коши // Электронное моделирование, т. 29, № 3, 2007. – С. 11-25.
