вверх
Українська   English
ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

Одной из основных проблем теоретической кибернетики является проблема взаимодействия управляющей и управляемой системы [1]. Основная проблематика для автоматов в лабиринтах группируется вокруг задач, называемых задачами синтеза и анализа. Задача синтеза состоит в описании тех автоматов и коллективов автоматов, которые обходят лабиринты из заданного класса. Главными объектами выступают конечные автоматы с камнями, коллективы автоматов, автоматы с магазинной памятью и другие. Задача анализа состоит в описании по заданному автомату или коллективу автоматов всех лабиринтов или всех лабиринтов определенного вида, которые обходятся этими автоматами. В качестве автоматов и лабиринтов выступают объекты, указанные в задаче синтеза. Продвижение в решении этой задачи по сравнению с задачей синтеза значительно скромнее и состоит, по существу, в построении различных позитивных и негативных примеров возможных соответствий между конкретными множествами лабиринтов и автоматов, обходящих в точности эти лабиринты, или же отсутствие таковых.

Одним из вариантов обхода является использование системы взаимодействующих агентов, называемой коллективом. Коллектив анализирует лабиринты с учетом положения его «членов» на графе [2],[3].

Одной из важных подзадач задачи анализа лабиринта является экономное представление информации о лабиринте.

В работе рассматривается прямоугольный лабиринт без дыр, мостов и точек сочленения, который однозначно описывается словом обхода этого лабиринта по внешнему контуру.

1. Цель и задачи исследования, планируемые результаты

Объектом исследования в работе является обход лабиринта по его контуру. Предметом исследования является метод представления слова обхода лабиринта по его контуру системой элементарных прямоугольных лабиринтов, что зачастую проще исходного слова.

Основной задачей данной работы является разработка и программная реализация метода оптимального разложения плоских прямоугольных графов и представление его формулой, описывающей лабиринт в виде системы прямоугольников.

2. Актуальность темы работы

Поскольку задача распознавания неизвестного конечного графа в общем случае является сложной и на сегодняшний день частично решенной, то рассматриваются частные случаи графов с заранее оговоренными входными условиями. Следовательно, алгоритмы для распознавания шахматного лабиринта применяются для составления топологических карт при решении задачи взаимодействия управляющей и управляемой систем.

Прикладная актуальность проблемы определяется тем, что проблема распознавания для шахматных лабиринтов далека от разрешения, и ее исследования находятся в зачаточном состоянии. Теоретическая важность и актуальность определяются тем, что распознавание таких лабиринтов проводится методами, аналогичными методам теории автоматов.

3. Основные определения

3.1 Прямоугольный лабиринт

Под прямоугольным лабиринтом понимается плоский неориентированный конечный связный граф G=(VG , EG, μ) без дыр, мостов и точек сочленения, множество вершин которого VG есть подмножество множества Z2 точек декартовой плоскости с целочисленными координатами. Пусть (x1,y1), (x2,y2) – две вершины. Они называются соседними, если |x1-x2|=1 и y1=y2 или |y1-y2|=1 и x1=x2.

X-траекторией назовем последовательность точек (x1,y1)(x2,y2)...(xi,yi)..., в которой xi+1=xi+1,y1=x2=...yi=... .Y-траекторией назовем последовательность точек (x1,y1)(x2,y2)...(xi, yi)..., в которой yi+1=yi+1,x1=x2=...xi=... . Лабиринт называется выпуклым, если любая X-траектория или Y-траектория не выходит за границы лабиринта.

На рисунке 3.1 приведен пример выпуклого лабиринта. Любая траектория – горизонтальная или вертикальная, проведенная в данном лабиринте не выходит за его границы, т.е. является внутренней.

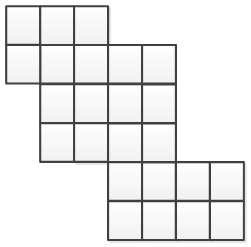
Рисунок 3.1 - Пример выпуклого лабиринта

Рисунок 3.1 - Пример выпуклого лабиринта

На рисунке 3.2 можно увидеть, что траектория, проведенная между вершинами a и b, является X-траекторией, которая выходит за границы лабиринта. Следовательно, данная траектория не является внутренней, а значит данный лабиринт – не выпуклый.

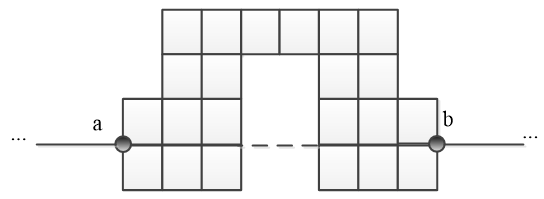
Рисунок 3.2 - Пример невыпуклого лабиринта

Рисунок 3.2 - Пример невыпуклого лабиринта

3.2 Слово обхода лабиринта

Обход лабиринта заключается в последовательном движении в коде Фримена (n - север, o - восток, s - юг, w -  запад), который описывает лабиринт по контуру с возвратом в начальную точку. Начальная точка лежит в северо – западном углу с минимальными координатами. Слово обхода по часовой стрелке составляется по направлению и суммы общих пройденных ребер, записывающихся в степени, до изменения направления (см. рис. 3.3). Из рисунка 3.3 видно, что слово обхода будет иметь следующий вид: v=oi sj wr nh wk nt.

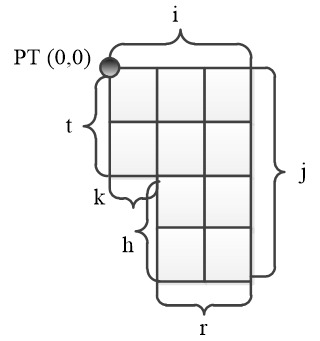
Рисунок 3.3 - Пример лабиринта c известными сторонами

Рисунок 3.3 - Пример лабиринта с известными сторонами

3.3 Система прямоугольников

Описание шахматного лабиринта в виде системы прямоугольников зачастую позволяет более экономно описать слово обхода и упростить выполнение операций, например, таких как вычисление площади лабиринта. Для описания шахматного лабиринта в виде системы прямоугольников, необходимо выделять максимальные по площади прямоугольники и описать систему полученных прямоугольников как единую структуру.

Каждый прямоугольник описывается количеством ребер по оси ординат (длиной), оси абсцисс (шириной) и координатой точки, которая показывает связь с оставшейся частью лабиринта. На рисунке 4 лабиринт представлен системой двух прямоугольников П1(3,2,(1,2)) и П2((1,2),2,2). В дальнейшем в П2 удобно вместо координат (1,2) писать число k=1, так называемый отступ по оси абсцисс от начальной точки, координаты которой всегда равны (0,0).

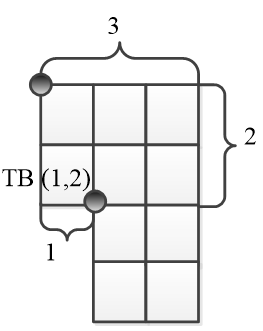
Рисунок 3.4 - Прямоугольник П(3,2)

Рисунок 3.4 - Прямоугольник П(3,2)

4. Проблема исследования свойств лабиринтов агентами

В дипломной работе Ю.Н. Стародубцевой [4] был предложен алгоритм распознавания квадратных мозаик коллективом автоматов. Предложенный алгоритм позволяет распознать выпуклый лабиринт типа полимино при помощи коллектива автоматов, который состоит из агента – исследователя и агента – экспериментатора. Алгоритм работы агента – экспериментатора реализован при помощи двух подагентов.

Агент – исследователь имеет камень, которым может помечать вершину или снимать камень с вершины. На каждом шагу агент – исследователь запоминает два параметра: предыдущее движение и текущий шаг. При обнаружении вершины, которая уже помечена камнем, агент – исследователь передает сообщение агенту – экспериментатору сообщение о конце движения. Агент – исследователь имеет конечную память.

Как было сказано выше, работа агента – экспериментатора реализована при помощи двух подагентов: АЭ1 и АЭ2. Агент АЭ1 принимает от агента – исследователя последовательность сообщений и переводит эту последовательность в слово обхода. Затем агент АЭ1 передает полученное слово агенту АЭ2, и агенты АЭ1 и АЭ2 начинают обрабатывать слово обхода и переводить его в изображение лабиринта в виде системы прямоугольников. Агенты АЭ1 и АЭ2 имеет конечную, но бесконечно наращиваемую память.

Между агентом – исследователем и АЭ1 существует однобокая связь: агент – исследователь может передавать сообщения агенту АЭ1, но не наоборот. Агенты АЭ1 и АЭ2 имеют двустороннюю связь.

Входными данными для алгоритма распознавания неизвестного лабиринта типа полимино при помощи коллектива автоматов является выпуклый плоский неориентированный конечный лабиринт типа полимино без дыр, мостов и точек сочленения. Коллектив автоматов, состоящий из агента – исследователя и двух подагентов – экспериментаторов должен на основе лабиринта построить его изображения в виде системы прямоугольников.

5. Метод построения представления однозначно определяющего лабиринт

Шаг 1. Агент помещается в произвольную вершину лабиринта и движется на север до граничной вершины лабиринта, помечая ее координатой.

Шаг 2. Агент обходит лабиринт по внешнему контуру по часовой стрелке, получает слово обхода (последовательность движений и слово координат пройденных вершин)[3]. Через µ(t) будем обозначать направление движения А из вершины t.

Для определения координат углов лабиринта А, агент движется по слову до смены буквы:

1) при µ(s)=nk координата y:=y+k, а x остаётся неизменным;

2) при µ(s)=ot координата x:=x+t, а y остаётся неизменным;

3) при µ(s)=sp координата y:=y-p, а x остаётся неизменным;

4) при µ(s)=wq координата x:=y-q, а y остаётся неизменным;

Шаг 3. По p и q определяем поле лабиринта, т.е. наименьший по площади прямоугольник, в который вписывается лабиринт.

Для нахождения границ поля находим координаты с минимальным и максимальным значением по x и по y среди координат углов, соответственно. Сумма их модулей является длиной и шириной поля. Сдвигаем поле и лабиринт в нем таким образом, чтобы верхний северо-западный угол поля получил координату (0,0) соответствующим образом меняя координаты вершин лабиринта. Следовательно, поле П((x,y)w,h) характеризуется координатой (x,y)=(0,0) северо-западного угла, шириной w и длиной h.

Шаг 4. По слову обхода лабиринта и полю выделяем из лабиринта часть, являющуюся прямоугольником максимальным по площади, касающуюся северной границы поля [4]. После выделения этого прямоугольника он удаляется из лабиринта. Получаем новый лабиринт. Доказано, что он является выпуклым лабиринтом без дыр и мостов. Для него строится новое слово обхода p и новое поле.

Шаг 4 выполняется до тех пор, пока слово обхода p не станет пустым. В результате по слову обхода получаем систему прямоугольников, покрывающих лабиринт.

Из вышесказанного следует, что на 4 шаге можно выбирать не только северную, но и любую другую границу поля. Очевидно, что полученная система прямоугольников существенно зависит от такого выбора на каждом шаге. В [4] предложен жадный алгоритм такого выбора. В п. 4 при этом строится четыре прямоугольника, выбирая северную, южную, восточную, западную стороны текущего поля. Затем среди четырех прямоугольников выбирается максимальный по площади.

Оптимальная стратегия выбора прямоугольника на шаге 4 является сложной комбинаторной задачей, требующей своего исследования.

Пример работы метода получения системы прямоугольников представлен на рисунке 5.1

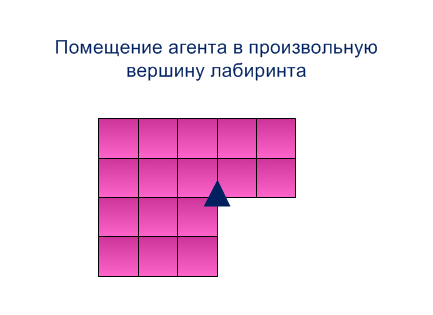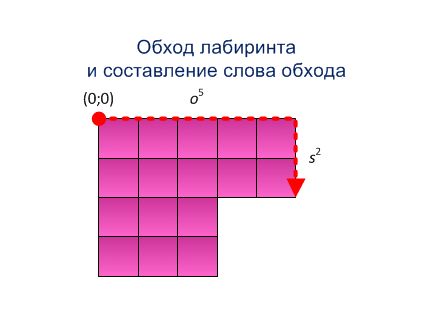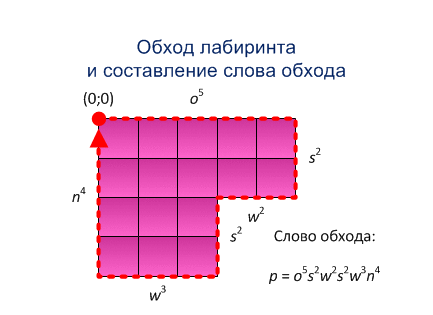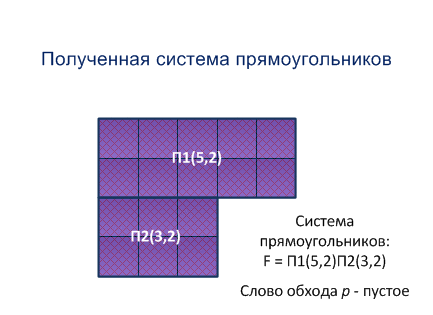
Рисунок 5.1 - Метод построения системы прямоугольников

Рисунок 5.1 - Метод построения системы прямоугольников (анимация: 15 кадров, размер - 433х315, 164 килобайт)

Выводы

Предложен новый метод разложения шахматного лабиринта в систему максимальных прямоугольников. Полученная система прямоугольников является разбиением исходного лабиринта. Примеры показывают, что зачастую целесообразно лабиринт представлять системой пересекающихся прямоугольников, которые образуют покрытие лабиринта. Оптимальный выбор такого покрытия является сложной комбинаторной проблемой, требующей своего исследования.

Предложенное изображение лабиринта позволяет облегчить подсчет численных параметров лабиринта, таких как площадь, длина контура и другое. Метод заключается в пошаговом выделении четырех прямоугольников, захватывая при этом северную, южную, восточную и западную с тороны. Затем среди четырех прямоугольников выбирается максимальный по площади и выделяется из слова обхода. Далее формируется новый обход оставшейся части лабиринта и новая рабочая точка. Метод продолжает работу до тех пор, пока слово обхода не станет пустым.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2014 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список источников

  1. Кудрявцев В.Б. Системы автоматов в лабиринтах / В.Б. Кудрявцев, Г. Килибарда, Ш. Ушумлич // Интеллектуальные системы – М. : Изд-во мех.-мат. ф-та МГУ. – Т. 10, вып. 1–4. – С. 449–564.
  2. Hoffman F. One pebble does not suffice to search plane labyrinths / Hoffman F. // Lecture Notes in Computer Science. – 1981. – V. 117. – P. 433–444.
  3. Blum M. On the power of the compass / M. Blum, D. Kozen // The Proceedings of the 19th Annual Symposium of Foundations of Computer Science. – 1978. – P. 132–142.
  4. Стародубцева Ю.Н. Исследование и разработка метода распознавания квадратных мозаик двумя автоматами: Дипломная работа. – ДонНТУ, 2012 г.
  5. Стародубцева Ю.Н. Распознавание шахматного лабиринта с помощью коллектива автоматов // Ю.Н. Стародубцева // V міжнар. наук.-практ. конф. молод. учених, аспірантів, студентів «Сучасна інформаційна Україна: інформатика, економіка, філософія» (12-13 травня 2011 р.). Том 1. – Донецьк, 2011. – С. 109–113.
  6. Белоус Ю.А. Жадный алгоритм разложения прямоугольного лабиринта без дыр в систему прямоугольников / Ю.А. Белоус, И.С. Грунский // Х Ювілейна міжн. наук. – практ. конф. «Математичне та програмне забезпечення інтелектуальних систем» (Дніпропетровськ 21-23 листопада 2012 року). – Дніпропетровськ, Дніпропетровський нац. ун-т імені Олеся Гончара 2012. – С. 24–25.
  7. Капитонова Ю.В. Математическая теория программирования вычислительных систем / Ю.В. Капитонова, А.А. Летичевский. – М.: Наука, 1988. – 296 с.
  8. Кудрявцев В.Б. Введение в теорию автоматов / В.Б. Кудрявцев, С.В. Алешин, А.С. Подколзин. – М. : Наука, 1985. – 320 с.
  9. Кудрявцев В.Б., Калибарда Г., Ушумлич Ш. Независимые системы автоматов в лабиринтах / В.Б. Кудрявцев, Калибарда Г., Ушумлич Ш. // «Дискретная математика» 2003 г., т. 15, вып. 3. – С. 3–40.
  10. Килибарда Г. О поведении автоматов в лабиринтах / Г. Килибарда, В.Б. Кудрявцев, Щ. Ушумлич // Дискретная математика. – Российская академия наук, 1992. – Т. 4, вып. 3. – С. 3–28.
  11. Голомб С.В. Полимино / Голомб С.В. – М. : Мир, 1975. – 207 с.
  12. Зыричев А.Н. О синтезе автомата, обходящего плоские лабиринты с ограниченными дырами / Зыричев А.Н. // Дискретная математика. – 1991. – Т. 3, вып. 1. – С. 105–113.
  13. Золотых А.А. Обход лабиринтов с ограниченными в фиксированных направлениях дырами / Золотых А.А. // Дискретная математика. – 1993. – Т. 5, вып. 1. – С. 59–69.
  14. Курдюмов Г.Л. Коллектив автоматов с универсальной проходимостью / Курдюмов Г.Л. // Проблемы передачи информации. – 1981. – Т. 17, вып. 4. – С. 601–604.