to top
Українська   Русский
DonNTU   Masters' portal

Content

Introduction

One of the main problems of theoretical cybernetics is the problem of interaction between controlling and controlled system. The main range of problems for automata in mazes deals with the tasks named tasks of analysis and synthesis. The task of synthesis is to describe those automata and collective of automata that bypass mazes of a given class. The main objects are finite automatons with calculi, collective of automata, pushdown automata, and others. The task of analysis is to describe for a given automaton or collective of automata all mazes or mazes of a certain type which are bypassed by these automata. The objects specified in the task of synthesis are automata and mazes. The progress in completing this task compared to the task of synthesis is slower and consists essentially in the construction of various positive and negative examples of possible matches between specific sets of mazes and automata bypassing exactly these mazes, or lack thereof.

One of the options is to use a bypass system of interacting agents called collective. Collective analyzes mazes based on the position of its "members" on the graph [2],[3].

One of the important subtasks of the analysis of the maze is economical presentation of the information on the maze.

This paper considers the rectangular labyrinth without holes, bridges and articulation points, which is uniquely described by the bypass word of this maze on the external circuit.

1. The object and tasks of the research work, expected results

The object of research in this paper is to bypass the maze of it's contour. The subject of research is the method of representation of the word in his labyrinth bypass circuit with the help of the system of elementary rectangular mazes, which is often simpler than the original word.

The main task of this work is the development and software realization of the method of optimal flat rectangular graphs decomposition and its presentation by the formula describing the maze as a system of rectangles.

2. Actuality of the research

Since the problem of recognizing an unknown finite graph in general is complex and partially solved until nowadays, the particular cases of graphs with pre-agreed input conditions are considered. Consequently, algorithms for recognition of chess labyrinth are used for making topo maps for solving the problem of interaction between controlling and controlled systems.

Applied actuality of the problem is determined by the fact that the problem of recognition for chess labyrinths is far from being resolved, and its research is in its infancy. Theoretical importance and relevance are determined by the fact that recognition of such labyrinths is performed by methods similar to the methods of the theory of automata.

3. Basic definitions

3.1 Rectangular maze

Rectangular maze means flat rectangular undirected finite connected graph G=(VG , EG, μ) without holes, bridges and articulation points, the vertex set of which VG is the subset of the set Z2 of the points on the Cartesian plane with integral coordinates. Let (x1,y1), (x2,y2) be two vertices. They are named adjacent if |x1-x2|=1 and y1=y2 or |y1-y2|=1 and x1=x2.

X-path is a sequence of points (x1,y1)(x2,y2)...(xi,yi)..., in which xi+1=xi+1,y1=x2=...yi=... .Y-path is a sequence of points (x1,y1)(x2,y2)...(xi, yi)..., in which yi+1=yi+1,x1=x2=...xi=... . The maze is named convex, if any X-path or Y-path does not overrun the maze.

Figure 3.1 shows an example of a convex maze. Any trajectory - horizontal or vertical, held in this maze does not overrun it, i.e. is internal.

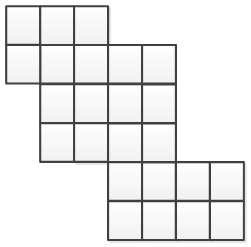
Figure 3.1 - Example convex maze

Figure 3.1 - Example convex maze

In figure 3.2 one can see that the path drawn between vertices a and b, is X-path, which overruns the maze. Therefore, this path is not internal, which means this maze is not convex.

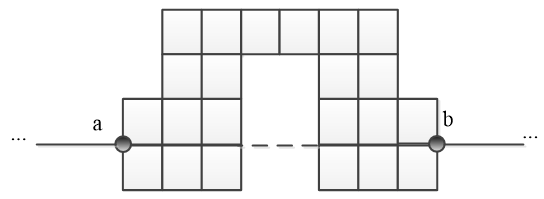
Figure 3.2 - Example of a non-convex maze

Figure 3.2 - Example of a non-convex maze

3.2 Maze bypass word

Bypass of the maze is a logical movement in Freeman code (n - north, o - east, s - south, w -  west),which describes the contour of the maze and returns to the starting point. Starting point lies in the north - west corner with minimal coordinates. Bypass word of the clockwise direction is made according to the direction and the amount of common traversed edges recorded in the degree, till the change of the direction (see Fig. 3.3). On Figure 3.3 one may see that the bypass word will be the following: v=oi sj wr nh wk nt.

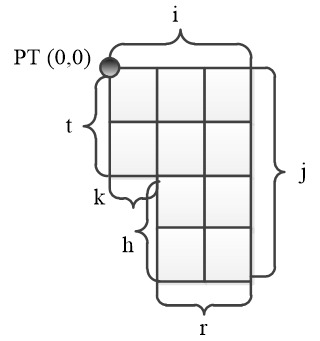
Figure 3.3 - Example maze known parties

Figure 3.3 - Example maze known parties

3.3 System of rectangles

Description of a chess maze as a system of rectangles often allows to describe the bypass word in a more economical way and to simplify operations, such as the calculation of the area of the maze. To describe chess maze as a system of rectangles, one must allocate the rectangles with maximum area, and describe the system of obtained rectangles as an integral structure.

Each rectangle is described by the number of edges on the vertical axis (length) x-axis (width) and the coordinate of the point, which shows the connection with the rest of the maze. In Figure 3.4 the maze is presented by a system of two rectangles P1(3,2,(1,2)) and P2((1,2),2,2). Further in P2 is convenient to replace the coordinates (1,2) by writing k=1, the so-called indentation along the horizontal axis from the starting point, the coordinates of which always equal (0,0).

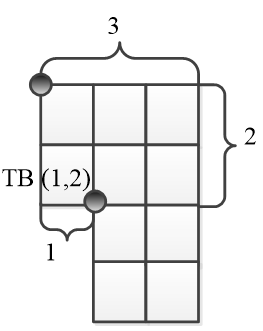
Figure 3.4 - Rectangle P(3,2)

Figure 3.4 - Rectangle P(3,2)

4. Problem of research of the properties of mazes by agents

In Y.N. Starodubtseva’s thesis work [4] has been proposed the algorithm of recognition of square mosaics by collective of automata. The proposed algorithm allows identifying a convex maze of polymino type using collective of automata, which consists of an agent-researcher and an agent-experimenter. Two subagents implement the algorithm of the work for the agent-experimenter.

The agent-researcher has a calculus which may mark the vertex or remove a calculus from the vertex. At each step the agent-researcher remembers two parameters: the previous movement and the current step. Upon detection of vertex, which is already marked by a calculus, the agent-researcher sends a message to the agent-experimenter about the end of the movement. Agent-researcher has finite memory.

As mentioned above , the work of an agent-experimenter is realized by two subagents : AE1 and AE2 . AE1 agent receives from the agent-researcher the sequence of messages and translates this sequence into a bypass word. Then the agent the resulting word to the agent AE1, and the agents AE1 and AE2 begin to process the bypass word to translate it into an image of the maze in the form of rectangles. The agents AE1 and AE2 have finite, but infinitely scalable memory.

There is a unilateral connection between the agent-researcher and AE1: the agent-researcher can send messages to the agent AE1 , but not vice versa. The agents AE1 and AE2 have bilateral connection.

The input data for the algorithm of detecting unknown maze of the type polyomino using collective of automata is a convex flat undirected finite maze of the type polyomino without holes, bridges and articulation points. The collective of automata, consisting of an agent-researcher and two subagents-experimenters should build the image of the maze in the form of rectangles on its basis.

5. Method for constructing a representation uniquely identifying the maze

Step 1. The agent is placed in an arbitrary vertex of the maze and moves northward to the boundary vertex of the maze, marking its coordinate.

Step 2. The agent bypasses clockwise on the external circuit, obtains the bypass word (sequence of movements and coordinate word of the traversed vertices) [3]. Through µ(t) we will denote the direction of movement A from the vertex t.

To determine the coordinates of the corners of the maze A, the agent moves through the word till the change of the letter:

1) if µ(s)=nk then the coordinate y:=y+k, а x stays permanent;

2) if µ(s)=ot then the coordinate x:=x+t, а y stays permanent;

3) if µ(s)=sp then the coordinate y:=y-p, а x stays permanent;

4) if µ(s)=wq then the coordinate x:=y-q, а y stays permanent;

Step 3. According to p and q the maze range is defined, i.e. the rectangle with the smallest area which the maze fits in.

To find the boundaries of the range one should find the coordinates of the minimum and maximum value for x and y among the coordinates of the angles, respectively. The sum of their modules is the length and width of the range. Move the range and the maze in it so that the upper northwest corner of the range received the coordinate (0,0) appropriately changing the coordinates of the vertices of the maze. Consequently, the range P((x,y)w,h) is characterized by the coordinate (x,y)=(0,0) of the north - west corner, width w and length h.

Step 4. According to the bypass word of the maze and the range we allocate a part of the maze, which is a rectangular with the maximum area regarding the northern boundary of the range [4]. After allocation of the rectangle it is removed from the maze. We get a new maze. It is proven that it is a convex maze without holes and bridges. We build a new bypass word p and a new range for it.

Step 4 is performed as long as the bypass word p becomes empty. As a result, according to the bypass word, we obtain a system of rectangles covering the maze.

From the above mentioned it follows that in Step 4, you can choose not only the north , but also any other range boundary . Obviously, the resulting system of rectangles essentially depends on this choice at each step. In [4] an algorithm for this choice is proposed. In p. 4 are constructed four rectangles, choosing the northern, southern, eastern , western side of the current range. Then, among the four rectangles, the one with the maximum area is selected.

The optimal strategy for the selection of the rectangle in step 4 is a complex combinatorial problem, requiring its research.

The example of the method for obtaining the rectangles is shown in Figure 5.1.

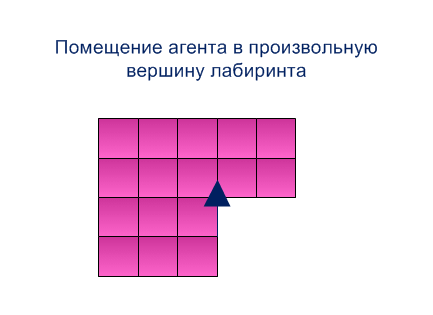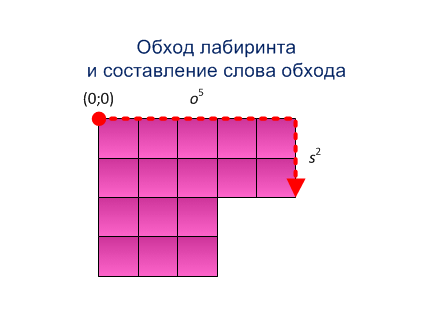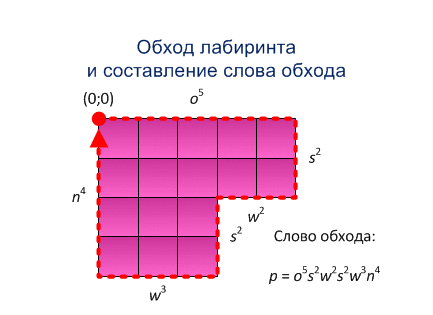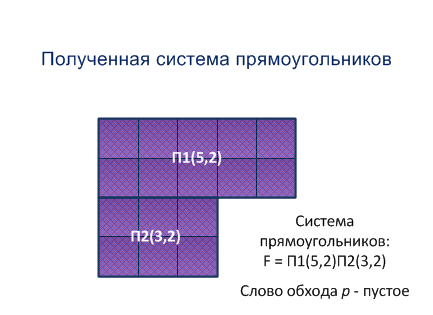
Figure 5.1 - Method for building the system of rectangles

Figure 5.1 - Method for building the system of rectangles (animation: 15 frames, size - 433х315, 164 kilobyte)

Conclusion

A new method for decomposition of the chess maze into a system of maximal rectangles is proposed. The resulting system of rectangles is a partition of the original maze. Examples show that it is often advisable to provide a maze with a system of intersecting rectangles that form a covering of the maze. The optimal choice of such covering is a complex combinatorial problem requiring its research.

The proposed image of the maze allows to facilitate calculation of the numeral parameters of the maze such as area, length of the circuit, etc. The method consists in step-by-step allocation of four rectangles, capturing the northern, southern, eastern and western sides. Then, among the four rectangles the one with the maximum area is selected and a bypass word is allocated. Next, a new bypass of the rest of the maze and a new operating point is formed. The method continues to work until the bypass word becomes empty..

During the publication of this essay, the master's thesis is not yet complete. Completion: December 2014. Full text of the work and materials on the topic can be obtained from the author or his manager after the indicated date.

References

  1. Кудрявцев В.Б. Системы автоматов в лабиринтах / В.Б. Кудрявцев, Г. Килибарда, Ш. Ушумлич // Интеллектуальные системы – М. : Изд-во мех.-мат. ф-та МГУ. – Т. 10, вып. 1–4. – С. 449–564.
  2. Hoffman F. One pebble does not suffice to search plane labyrinths / Hoffman F. // Lecture Notes in Computer Science. – 1981. – V. 117. – P. 433–444.
  3. Blum M. On the power of the compass / M. Blum, D. Kozen // The Proceedings of the 19th Annual Symposium of Foundations of Computer Science. – 1978. – P. 132–142.
  4. Стародубцева Ю.Н. Исследование и разработка метода распознавания квадратных мозаик двумя автоматами: Дипломная работа. – ДонНТУ, 2012 г.
  5. Стародубцева Ю.Н. Распознавание шахматного лабиринта с помощью коллектива автоматов // Ю.Н. Стародубцева // V міжнар. наук.-практ. конф. молод. учених, аспірантів, студентів «Сучасна інформаційна Україна: інформатика, економіка, філософія» (12-13 травня 2011 р.). Том 1. – Донецьк, 2011. – С. 109–113.
  6. Белоус Ю.А. Жадный алгоритм разложения прямоугольного лабиринта без дыр в систему прямоугольников / Ю.А. Белоус, И.С. Грунский // Х Ювілейна міжн. наук. – практ. конф. «Математичне та програмне забезпечення інтелектуальних систем» (Дніпропетровськ 21-23 листопада 2012 року). – Дніпропетровськ, Дніпропетровський нац. ун-т імені Олеся Гончара 2012. – С. 24–25.
  7. Капитонова Ю.В. Математическая теория программирования вычислительных систем / Ю.В. Капитонова, А.А. Летичевский. – М.: Наука, 1988. – 296 с.
  8. Кудрявцев В.Б. Введение в теорию автоматов / В.Б. Кудрявцев, С.В. Алешин, А.С. Подколзин. – М. : Наука, 1985. – 320 с.
  9. Кудрявцев В.Б., Калибарда Г., Ушумлич Ш. Независимые системы автоматов в лабиринтах / В.Б. Кудрявцев, Калибарда Г., Ушумлич Ш. // «Дискретная математика» 2003 г., т. 15, вып. 3. – С. 3–40.
  10. Килибарда Г. О поведении автоматов в лабиринтах / Г. Килибарда, В.Б. Кудрявцев, Щ. Ушумлич // Дискретная математика. – Российская академия наук, 1992. – Т. 4, вып. 3. – С. 3–28.
  11. Голомб С.В. Полимино / Голомб С.В. – М. : Мир, 1975. – 207 с.
  12. Зыричев А.Н. О синтезе автомата, обходящего плоские лабиринты с ограниченными дырами / Зыричев А.Н. // Дискретная математика. – 1991. – Т. 3, вып. 1. – С. 105–113.
  13. Золотых А.А. Обход лабиринтов с ограниченными в фиксированных направлениях дырами / Золотых А.А. // Дискретная математика. – 1993. – Т. 5, вып. 1. – С. 59–69.
  14. Курдюмов Г.Л. Коллектив автоматов с универсальной проходимостью / Курдюмов Г.Л. // Проблемы передачи информации. – 1981. – Т. 17, вып. 4. – С. 601–604.