Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Мета і задачі дослідження, заплановані результати
- 2. Актуальність теми роботи
- 3. Основні визначення
- 3.1 Прямокутний лабіринт
- 3.2 Слово обходу лабіринту
- 3.3 Система прямокутників
- 4. Проблема дослідження властивостей лабіринтів агентами
- 5. Метод побудови представлення однозначно визначального лабіринт
- Висновки
- Перелік посилань
Вступ
Однією з основних проблем теоретичної кібернетики є проблема взаємодії керуючої і керованої системи. Основна проблематика для автоматів у лабіринтах групується навколо задач, званих задачами синтезу та аналізу. Задача синтезу полягає в описі тих автоматів і колективів автоматів, які обходять лабіринти із заданого класу. Головними об'єктами виступають кінцеві автомати з каменями, колективи автоматів, автомати з магазинною пам'яттю та інші. Задача аналізу полягає в описі по заданому автомату чи колективу автоматів всіх лабіринтів або всіх лабіринтів певного виду, які обходяться цими автоматами. В якості автоматів і лабіринтів виступають об'єкти, зазначені в задачі синтезу. Просування у вирішенні цієї задачі в порівнянні з задачею синтеза значно скромніше і складається, по суті, у побудові різних позитивних і негативних прикладів можливих відповідностей між конкретними множинами лабіринтів і автоматів , що обходять в точності ці лабіринти , або ж відсутність таких.
Одним з варіантів обходу є використання системи взаємодіючих агентів, званої колективом. Колектив аналізує лабіринти з урахуванням положення його «членів» на графі. [2],[3].
Однією з важливих подзадач задачі аналізу лабіринту є економне подання інформації про лабіринт.
У роботі розглядається прямокутний лабіринт без дірок, мостів і точок зчленування, який однозначно описується словом обходу цього лабіринту по зовнішньому контуру.
1. Мета і задачі дослідження, заплановані результати
Об'єктом дослідження в роботі є обход лабіринту по його контуру. Предметом дослідження є метод уявлення слова обходу лабіринту по його контуру системою елементарних прямокутних лабіринтів, що найчастіше простіше вихідного слова.
Основною задачею даної роботи є розробка та програмна реалізація методу оптимального розкладу плоских прямокутних графів і уявлення його формулою, яка описує лабіринт у вигляді системи прямокутників.
2. Актуальність теми роботи
Оскільки задача розпізнавання невідомого кінцевого графа в загальному випадку є складною і на сьогоднішній день частково вирішеною, то розглядаються окремі випадки графів з заздалегідь обумовленими вхідними умовами. Отже, алгоритми для розпізнавання шахового лабіринту застосовуються для складання топологічних карт при вирішенні завдання взаємодії керуючої і керованої систем.
Прикладна актуальність проблеми визначається тим, що проблема розпізнавання шахових лабіринтів далека від вирішення, і її дослідження знаходяться в зародковому стані. Теоретична важливість і актуальність визначаються тим, що розпізнавання таких лабіринтів проводиться методами, аналогічними методам теорії автоматів.
3. Основні визначення
3.1 Прямокутний лабіринт
Під прямокутним лабіринтом розуміється плоский неорієнтований кінцевий зв'язний граф G=(VG , EG, μ) без дірок, мостів і точок зчленування, множина вершин якого VG є підмножина множини Z2 точок декартової площини з цілочисельними координатами. Нехай (x1,y1), (x2,y2) – дві вершини. Вони називаються сусідніми, якщо |x1-x2|=1 и y1=y2 или |y1-y2|=1 и x1=x2.
X-траєкторією назвемо послідовність точок (x1,y1)(x2,y2)...(xi,yi)..., у якій xi+1=xi+1,y1=x2=...yi=... .Y-траєкторією назвемо послідовність точок (x1,y1)(x2,y2)...(xi, yi)..., у якій yi+1=yi+1,x1=x2=...xi=... . Лабіринт називається опуклим, якщо будь-яка X-траєкторія або Y-траєкторія не виходить за межі лабіринту.
На рисунку 3.1 наведено приклад опуклого лабіринту. Будь-яка траєкторія - горизонтальна або вертикальна, проведена в даному лабіринті не виходить за його межі, тобто є внутрішньою.
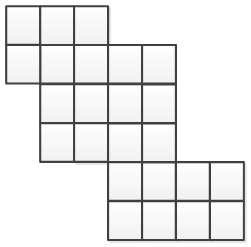
Рисунок 3.1 - Приклад опуклого лабіринту
На рисунку 3.2 можна побачити, що траєкторія, яка проведена між вершинами a і b, є X-траєкторією, яка виходить за межі лабіринту. Отже, дана траєкторія не є внутрішньою, а значить даний лабіринт - опуклий.
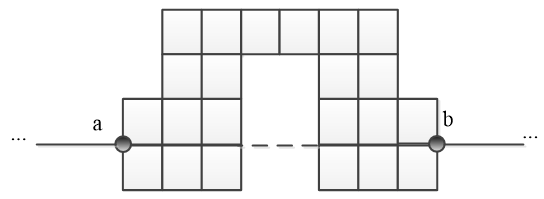
Рисунок 3.2 - Приклад неопуклого лабіринту
3.2 Слово обходу лабіринту
Обхід лабіринту полягає в послідовному русі в коді Фрімена (n - північ, o - схід, s - південь, w - захід), який описує лабіринт по контуру з поверненням в початкову точку. Початкова точка лежить в північно - західному куті з мінімальними координатами. Слово обходу за годинниковою стрілкою складається за напрямком та суми загальних пройдених ребер, що записуються в ступені, до зміни напрямку (див. рис. 3). З малюнка 3.3 можна побачити, що слово обходу буде мати наступний вигляд: v=oi sj wr nh wk nt.
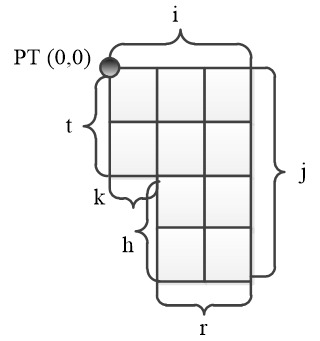
Рисунок 3.3 - Приклад лабіринту з відомими сторонами
3.3 Система прямокутників
Опис шахового лабіринту у вигляді системи прямокутників часто дозволяє більш економно описати слово обходу і спростити виконання операцій, наприклад, таких як обчислення площі лабіринту. Для опису шахового лабіринту у вигляді системи прямокутників, необхідно виділяти максимальні за площею прямокутники і описати систему отриманих прямокутників як єдину структуру.
Кожен прямокутник описується кількістю ребер по осі ординат (довжиною), осі абсцис (шириною) і координатою точки, яка показує зв'язок з залишеною частиною лабіринту. На рисунку 3.4 лабіринт представлений системою двох прямокутників П1(3,2,(1,2)) и П2((1,2),2,2). Надалі в П2 зручно замість координат (1,2) писати число k=1, так званий відступ по осі абсцис від початкової точки, координати якої завжди рівні (0,0).
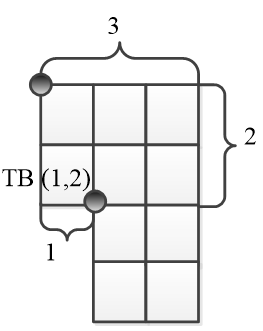
Рисунок 3.4 - Прямокутник П(3,2)
4. Проблема дослідження властивостей лабіринтів агентами
У дипломній роботі Ю.М. Стародубцевої [4] був запропонований алгоритм розпізнавання квадратних мозаїк колективом автоматів. Запропонований алгоритм дозволяє розпізнати опуклий лабіринт типу поліміно за допомогою колективу автоматів, який складається з агента - дослідника і агента - експериментатора. Алгоритм роботи агента - експериментатора реалізований за допомогою двох подагентів.
Агент - дослідник має камінь, яким може позначати вершину або знімати камінь з вершини. На кожному кроці агент - дослідник запам'ятовує два параметри: попередній рух і поточний крок. При виявленні вершини, яка вже позначена каменем, агент - дослідник передає повідомлення агенту - експериментатору повідомлення про кінець руху. Агент - дослідник має кінцеву пам'ять.
Як було сказано вище, робота агента - експериментатора реалізована за допомогою двох подагентов: АЕ1 і АЕ2. Агент АЕ1 приймає від агента - дослідника послідовність повідомлень і переводить цю послідовність в слово обходу. Потім агент АЕ1 передає отримане слово агенту АЕ2, і агенти АЕ1 і АЕ2 починають обробляти слово обходу і переводити його в зображення лабіринту у вигляді системи прямокутників. Агенти АЕ1 і АЕ2 мають кінцеву, але нескінченно нарощувану пам'ять.
Між агентом - дослідником і АЕ1 існує однобокий зв'язок: агент - дослідник може передавати повідомлення агенту АЕ1, але не навпаки. Агенти АЕ1 і АЕ2 мають двосторонній зв'язок.
Вхідними даними для алгоритму розпізнавання невідомого лабіринту типу поліміно за допомогою колективу автоматів є опуклий плоский неорієнтований кінцевий лабіринт типу поліміно без дірок, мостів і точок зчленування. Колектив автоматів, що складається з агента - дослідника і двох подагентов - експериментаторів повинен на основі лабіринту побудувати його зображення у вигляді системи прямокутників.
5. Метод побудови представлення однозначно визначального лабіринт
Крок 1. Агент поміщується в довільну вершину лабіринту і рухається на північ до граничної вершини лабіринту , позначаючи її координатою.
Крок 2. Агент обходить лабіринт по зовнішньому контуру за годинниковою стрілкою, отримує слово обходу (послідовність рухів і слово координат пройдених вершин) [3]. Через µ(t) будемо позначати напрямок руху А з вершини t.
Для определения координат углов лабиринта А, агент движется по слову до смены буквы:
1) при µ(s)=nk координата y:=y+k, а x залишається незмінним;
2) при µ(s)=ot координата x:=x+t, а y залишається незмінним;
3) при µ(s)=sp координата y:=y-p, а x залишається незмінним;
4) при µ(s)=wq координата x:=y-q, а y залишається незмінним;
Крок 3. По p и q визначаємо поле лабіринту , тобто найменший за площею прямокутник, в який вписується лабіринт.
Для знаходження меж поля знаходимо координати з мінімальним і максимальним значенням за x и по y серед координат кутів, відповідно. Сума їх модулів є довжиною і шириною поля. Зсуваємо поле і лабіринт у ньому таким чином, щоб верхній північно - західний кут поля отримав координату (0,0) відповідним чином змінюючи координати вершин лабіринту. Отже, поле П((x,y)w,h) характеризується координатою (x,y)=(0,0) північно - західного кута, шириною w й довжиною h.
Крок 4. По слову обходу лабіринту і полю виділяємо з лабіринту частину, що є прямокутником максимальним за площею, який стосується північного кордону поля [4]. Після виділення цього прямокутника він видаляється з лабіринту. Отримуємо новий лабіринт. Доведено, що він є опуклим лабіринтом без дір і мостів. Для нього будується нове слово обходу p й нове поле.
Крок 4 виконується доти, поки слово обходу p не стане порожнім. У результаті за словом обходу отримуємо систему прямокутників, що покривають лабіринт.
З вищесказаного випливає, що на 4 кроці можна вибирати не тільки північну, але і будь-який інший кордон поля. Очевидно, що отримана система прямокутників істотно залежить від такого вибору на кожному кроці. У [4] запропонований жадний алгоритм такого вибору. У п. 4 при цьому будується чотири прямокутники, вибираючи північну, південну, східну, західну сторони поточного поля. Потім серед чотирьох прямокутників обирається максимальний по площі.
Оптимальна стратегія вибору прямокутника на кроці 4 є складною комбінаторною задачею, що вимагає свого дослідження.
Приклад роботи методу побудови системи прямокутників представлен на рисунку 5.1
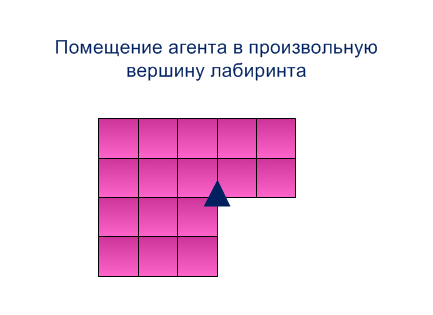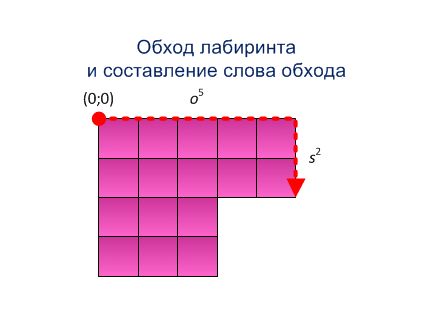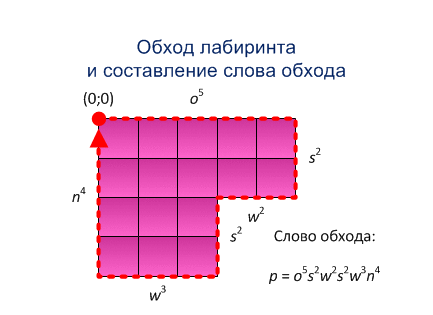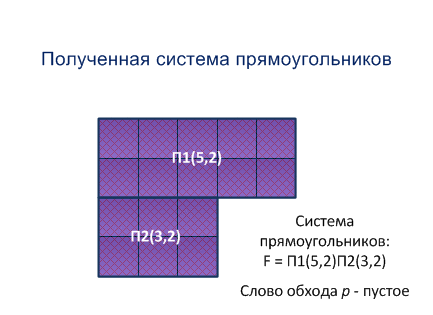
Рисунок 5.1 - Метод побудови системи прямокутників (анімація: 15 кадрів, розмір - 433х315, 164 кілобайта)
Висновки
Запропоновано новий метод розкладання шахового лабіринту в систему максимальних прямокутників. Отримана система прямокутників є розбиттям вихідного лабіринту. Приклади показують, що часто доцільно лабіринт представляти системою пересічних прямокутників, які утворюють покриття лабіринту. Оптимальний вибір такого покриття є складною комбінаторної проблемою, що вимагає свого дослідження.
Запропоноване зображення лабіринту дозволяє полегшити підрахунок чисельних параметрів лабіринту , таких як площа, довжина контуру та інше. Метод полягає в покроковому виділенні чотирьох прямокутників, захоплюючи при цьому північну, південну, східну і західну сторони. Потім серед чотирьох прямокутників обирається максимальний по площі і виділяється зі слова обходу. Далі формується новий обхід решти лабіринту і нова робоча точка. Метод продовжує роботу до тих пір, поки слово обходу не стане порожнім
При написанні цього реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2014 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Перелік посилань
- Кудрявцев В.Б. Системы автоматов в лабиринтах / В.Б. Кудрявцев, Г. Килибарда, Ш. Ушумлич // Интеллектуальные системы – М. : Изд-во мех.-мат. ф-та МГУ. – Т. 10, вып. 1–4. – С. 449–564.
- Hoffman F. One pebble does not suffice to search plane labyrinths / Hoffman F. // Lecture Notes in Computer Science. – 1981. – V. 117. – P. 433–444.
- Blum M. On the power of the compass / M. Blum, D. Kozen // The Proceedings of the 19th Annual Symposium of Foundations of Computer Science. – 1978. – P. 132–142.
- Стародубцева Ю.Н. Исследование и разработка метода распознавания квадратных мозаик двумя автоматами: Дипломная работа. – ДонНТУ, 2012 г.
- Стародубцева Ю.Н. Распознавание шахматного лабиринта с помощью коллектива автоматов // Ю.Н. Стародубцева // V міжнар. наук.-практ. конф. молод. учених, аспірантів, студентів «Сучасна інформаційна Україна: інформатика, економіка, філософія» (12-13 травня 2011 р.). Том 1. – Донецьк, 2011. – С. 109–113.
- Белоус Ю.А. Жадный алгоритм разложения прямоугольного лабиринта без дыр в систему прямоугольников / Ю.А. Белоус, И.С. Грунский // Х Ювілейна міжн. наук. – практ. конф. «Математичне та програмне забезпечення інтелектуальних систем» (Дніпропетровськ 21-23 листопада 2012 року). – Дніпропетровськ, Дніпропетровський нац. ун-т імені Олеся Гончара 2012. – С. 24–25.
- Капитонова Ю.В. Математическая теория программирования вычислительных систем / Ю.В. Капитонова, А.А. Летичевский. – М.: Наука, 1988. – 296 с.
- Кудрявцев В.Б. Введение в теорию автоматов / В.Б. Кудрявцев, С.В. Алешин, А.С. Подколзин. – М. : Наука, 1985. – 320 с.
- Кудрявцев В.Б., Калибарда Г., Ушумлич Ш. Независимые системы автоматов в лабиринтах / В.Б. Кудрявцев, Калибарда Г., Ушумлич Ш. // «Дискретная математика» 2003 г., т. 15, вып. 3. – С. 3–40.
- Килибарда Г. О поведении автоматов в лабиринтах / Г. Килибарда, В.Б. Кудрявцев, Щ. Ушумлич // Дискретная математика. – Российская академия наук, 1992. – Т. 4, вып. 3. – С. 3–28.
- Голомб С.В. Полимино / Голомб С.В. – М. : Мир, 1975. – 207 с.
- Зыричев А.Н. О синтезе автомата, обходящего плоские лабиринты с ограниченными дырами / Зыричев А.Н. // Дискретная математика. – 1991. – Т. 3, вып. 1. – С. 105–113.
- Золотых А.А. Обход лабиринтов с ограниченными в фиксированных направлениях дырами / Золотых А.А. // Дискретная математика. – 1993. – Т. 5, вып. 1. – С. 59–69.
- Курдюмов Г.Л. Коллектив автоматов с универсальной проходимостью / Курдюмов Г.Л. // Проблемы передачи информации. – 1981. – Т. 17, вып. 4. – С. 601–604.
