Українська   English
ДонНТУ   Портал магистров

Реферат по теме випускной работы

Содержание

Введение

В настоящее время актуальны задачи, связанные с анализом и синтезом языков, представимых в помеченных графах. Интерес к изучению таких графов вызван тем, что существует ряд важных задач, которые естественным образом представляются в виде помеченных графов. Такие графы интенсивно изучаются при верификации программ и планировании движения мобильного робота [1].

Свойства языков, представимых графами с отмеченными дугами, изучались С. Клини. Им предложена широкоизвестная алгебра, описывающая эти языки. В настоящее время известен ряд алгоритмов описания этих языков в алгебре Клини и построение графов по такому описанию [2]. Были предложены алгебры, аналогичные алгебре Клини, для описания языков, порожденных такими графами, и алгоритмы перехода от алгебраических выражений, описывающих языки, к представляющим их графам и наоборот. Также был разработан и предложен алгоритм построения регулярного выражения по заданному помеченному графу [1]. В данной работе предлагается усовершенствовать вышеуказанный алгоритм, найти закономерности в строении графов и построении регулярного выражения по ним.

1. Актуальность темы

На данный момент существует два типа алгоритмов построения регулярного выражения по помеченному графу: А) решение системы линейных уравнений; Б) преобразование графа. Идея преобразования графа, заключающаяся в сокращении его вершин и дуг, впервые была изложена в книге Хопкрофта «Введение в теорию автоматов, языков и вычислений» [2]. Метод последовательного удаления вершин, как и метод решения систем линейных уравнений для построения регулярного выражения, является достаточно сложным. Трудность заключается в том, что если этот метод применяется на больших графах, то растет количество итераций выполняемого алгоритма. Количество итераций алгоритма зависит от порядка удаления вершин и дуг. Задача оптимального удаления вершин и дуг до сих пор не решена. Ногина Н.В. предложила исключать те вершины, которые являются преходящими в финальную [1].

Магистерская работа посвящена актуальной научной задаче построения регулярного выражения по заданному помеченному графу и усовершенствованию уже существующего алгоритма.

2. Цель и задачи исследования, планируемые результаты

Целью данной квалификационной работы является выделение частных случаев подграфов, для которых предлагается порядок эффективного удаления вершин и дуг. Эти методы являются эвристическими методами построения регулярного выражения.

Основной задачей данной работы является усовершенствование и программная реализация алгоритма построения регулярного выражения по заданному графу.

Объект исследования: построение регулярного выражения по заданному помеченному графу

Предмет исследования: метод построения регулярного выражения по заданному помеченному графу, основанный на последовательной редукции вершин графа.

3. Теоретические сведения

3.1 Основные определения и обозначения

Граф – это совокупность объектов со связями между ними. Объекты рассматриваются как вершины, или узлы графа, а связи – как дуги, или ребра. Для различных областей использования виды графов могут отличаться ориентируемостью, ограничениями на количество связей и дополнительными данными о вершинах или ребра. Большое количество структур, которые имеют практическую ценность в математике и информатике, могут быть представлены графами.

Граф G – это упорядоченная пара G = (V; E), для которой выполняются следующие условия: V – множество вершин или узлов E – множество пар (в случае неориентированного графа – неупорядоченных) вершин, которые называют ребрами V и E обычно считаются конечными множествами. Основные элементы графа состоят из вершин графа, ребер графа и дуг графа. Сочетание этих элементов определяет понятия: неориентированный граф, ориентированный граф и смешанный граф.

Неориентированный граф – это граф, для каждого ребра которого несуществен порядок двух его конечных вершин. Ориентированный граф – это граф, для каждого ребра которого существенен порядок двух его конечных вершин. Смешанный граф – это граф, содержащий как ориентированные, так и неориентированных ребра. Любой из перечисленных видов графа может содержать одно или несколько ребер, у которых оба конца сходятся в одной вершине, такие ребра называются петлями. Если пара вершин соединяется несколькими ребрами или дугами одного направления, то ребра (дуги) называют кратными (параллельными). Дуга или ребро соединяющий вершину саму с собой называется петлей. Граф без кратных дуг и петель называется простым.

Степень вершины – количество ребер графа G, инцидентных вершине x. Вес ребра – значение, поставлены в соответствие данному ребру взвешенного графа. Обычно вес – действительное число, в таком случае его можно интерпретировать как «длину» ребра. Граф, в котором каждому ребру (каждой дуге) поставлено в соответствие определенное неотрицательное число, которое называют весом или длиной ребра (дуги), называют взвешенным графом. Путем в графе называют конечную последовательность вершин, в которой каждая вершина соединена ребром с последующей в последовательности вершин.

Дуги, имеющие общие конечные вершины, называются смежными. Путь (или цикл) называют простым, если ребра в нем не повторяются; элементарным, если он простой и вершины в нем не повторяются. Ориентированным путем в орграф называют конечную последовательность вершин V i, для которой все пары (Vi, V i + 1) есть (ориентированными) ребрами. Длиной пути (машрут) во взвешенном графе называют сумму длин звеньев этого пути (машрут).

Количество k ребер в пути называется длиной пути. Говорят, что этот путь соединяет вершины v1 и vk +1 или ведет с вершины v1 в вершину vk +1.Путем длины 0 считается последовательность, состоящая из единственной вершины. Путь, в котором все ребра попарно различны, называется цепью. Путь, в котором все промежуточные вершины попарно различны, называется простой цепью. Путь называют циклом, если в нем первая и последняя вершины совпадают.

Помеченным графом назовем восьмерку G = (Q, E, X, Y, μ, π, q0, F), где Q – конечное множество вершин, E – множество дуг, X – множество отметок вершин, Y – множество отметок дуг, μ: Q → X – функция разметки вершин, π: L → Y – функция разметки дуг, q0 – начальная вершина графа, F – множество финальных вершин.

Пусть Pre(qi) – множество начальных вершин всех дуг, входящих в qi, Post(qi) – множество конечных вершин всех дуг, исходящих из qi.

Преходящей вершиной назовем вершину q ≠ q0, у которой Pre(q)= Æ, висячей – q ≠ fin,у которой Post(q)=Æ.

Пусть Z множество всех непустых слов вида. Рассмотрим алгебру ,⊛,, в которой операции на языках L1, L2, L Í Z+ определены следующим образом:

1) операция объединения: V;

2) операция сочленения (склеивания): °;

3) операция итерации (зацикливания): L⊛ =, где L0= LначLкон, причем Lнач={x| xw=L, x=X}, Lкон= {x|w’=L,x=X}; L1=L; Ln+1=Ln◦L для всеx n≥1.

Регулярные выражения определим индуктивно:

1) пустое множество Æ является регулярным выражением;

2) x, xyx’ Являются регулярными выражениями для всех символов x,x’=X, y = Y;

3) если pи qрегулярные выражения, то выражения p◦q, pq, p⊛ также являются регулярными.

3.2 Представление графов. Матрица смежности

Для представления ориентированных графов можно использовать различные структуры данных. Выбор структуры данных зависит от операторов, которые будут применяться к вершинам и дугам орграфа. Одним из наиболее общих представлений орграфа G = (V, Е) является матрица смежности. Предположим, что множество вершин V = {1, 2, ..., n}. Матрица смежности для орграфа G — это матрица А разме-ра n х n со значениями булевого типа, где A[i][j] = true тогда и только тогда, когда существует дуга из вершины i в вершину j. Часто в матрицах смежности значение true заменяется на 1, а значение false — на 0. Время доступа к элементам матрицы смежности зависит от размеров множества вершин и множества дуг. Представление орграфа в виде матрицы смежности удобно применять в тех алгоритмах, в которых надо часто проверять существование данной дуги.

Обобщением описанного представления орграфа с помощью матрицы смежности можно считать представление помеченного орграфа также посредством матрицы смежности, но у которой элемент А[i][j] равен метке дуги i > j.

Если дуги от верши¬ны i к вершине j не существует, то значение A[i][j] не может быть значением какой-либо допустимой метки, а может рассматриваться как "пустая" ячейка.

Ниже(рис. 1) показана матрица смежности для помеченного орграфа, который был изображен ранее.

Здесь дуги представлены меткой символьного типа, а пробел используется при отсутствии дуг. Основной недостаток матриц смежности заключается в том, что она требует ?(n2) объема памяти, даже если дуг значительно меньше, чем n2. Поэтому для чтения мат¬рицы или нахождения в ней необходимого элемента требуется время порядка O(n2), что не позволяет создавать алгоритмы с временем O(n) для работы с орграфами, имеющими порядка O(n) дуг.

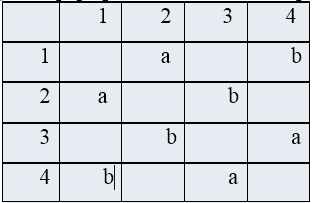
Алгоритм преобразования графа, путем сокращения его дуг и вершин

Рисунок 1 – Матрица смежности

3.3 Алгоритм построения регулярного выражения

Вход. Граф Gс отмеченными вершинами, сначальной и финальными вершинами.

Выход.Регулярное выражение языка, порожденного исходным графом.

Шаг 1. Граф Gпревращается в граф с отмеченными дугами. Для этого отметки вершин стираются и в дугах (qi, ei, qj)отметкой ei становится xiyixj, где xk=m(qk), где k=i,j, yi=ρ(ei).

В список вершин вводится фиктивная конечная вершина fin, а в список дуг – дуга из каждой финальной вершины qi в вершину fin с отметкой вершины qi.

Шаг 2. Удаление преходящих и висячих вершин.

While в графе существует вершина q ≠ q0, у которой Pre(qi)=Æ do

Удаляем вершину qiи все дуги,исходящие из нее;

While в графе существует вершина qi≠ fin, у которой Post(qi) = Æ do

Удаляем вершину qi и все дуги, входящие в нее;

Шаг 3. If в графе существует хоть одна петля или существуют вершины, не являющиеся начальными, из которых исходит хоть одна дуга, then goto Шаг 4

else goto Шаг 7;

Шаг 4. Удаление кратных дуг и петель.

1. Удаляем кратные дуги, заменяя их одной дугой с отметкой, равной объеди­нению отметок исходных дуг.

2. Удаляем все петли по следующему правилу.

Пусть в вершине qi есть петля с отметкой А. Если из этой вершины нет дуги в другую вершину, то петля удаляется. В противном случае для всех дуг (qi, ei, qj), где i≠j, с отметкой дуги В, петля удаляется, а отметка В заменяется отметкой А⊛, В ○ В.

На шагах 5 – 6 происходит удаление одной вершины.

Шаг 5.

Выбираем qi = Pre(fin);

q := qi; 

Шаг 6.

If q ¹ q0 then удаляем вершину q и все входящие и выходящие из нее дуги. Если при этом есть произвольный путь из некоторой вершины qi в вершину qk, через удаляемую вершину q, где qj принадлежит Pre(q) и qk принадлежит Post(q), то в граф добавляется дуга, со­держащая пометку, равную склеиванию пометок удаляемых дуг данного пути;

goto Шаг 2;

else qi равная q0 не исключается;

выбираем qm =Pre(q0);

q := qm;

goto Шаг 6;

Шаг 7. Удаляем все вершины q != q0 и q != fin и все входящие в них дуги. Получим граф, состоящий из двух вершин: q0 и fin и дуги, между ними с пометкой R, где R – это искомое регулярное выражение.

Ниже приведен алгоритм построения регулярного выражения по помеченному графу(рис.2)

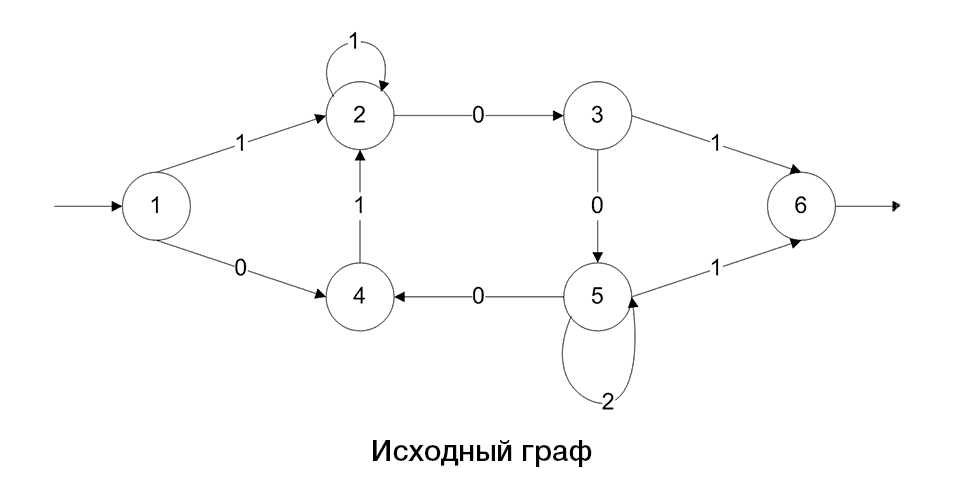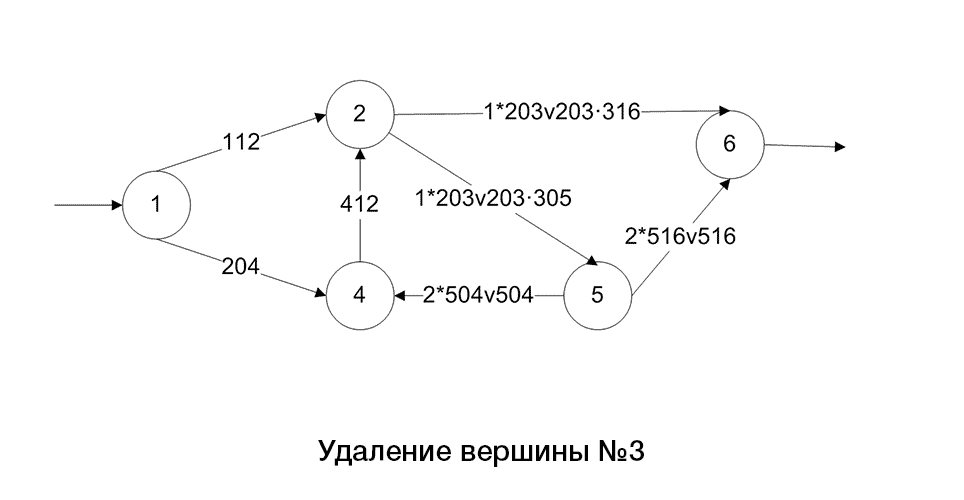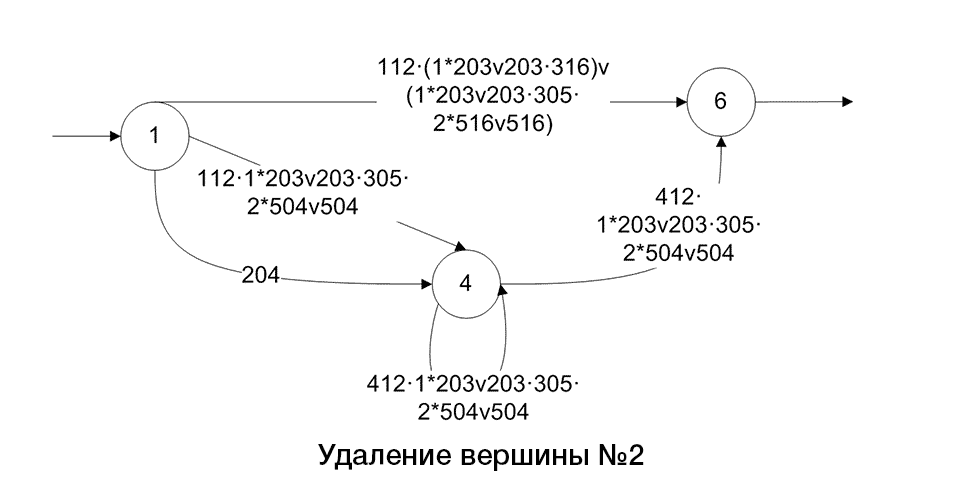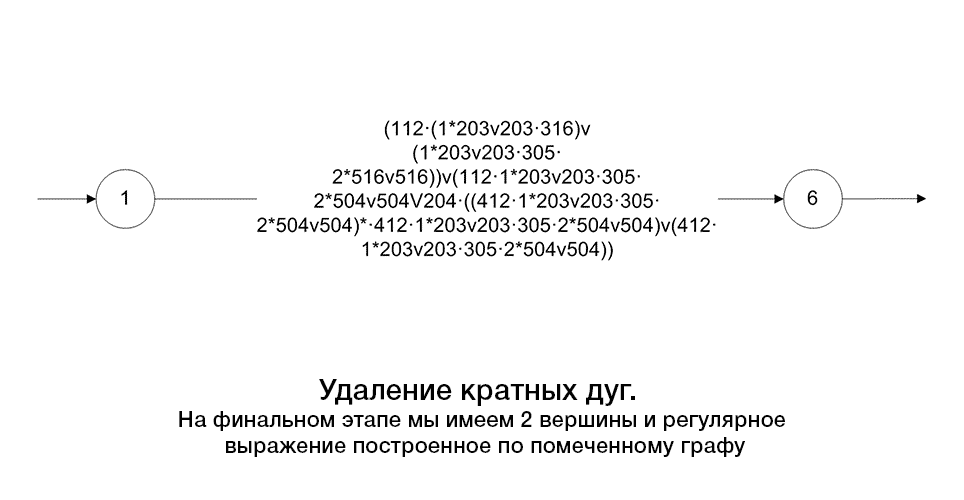
Алгоритм преобразования графа, путем сокращения его дуг и вершин

Рисунок 2 – Алгоритм преобразования графа, путем сокращения его дуг и вершин
(анимация: 10 кадров, 5 циклов повторения, 108 килобайт)

Виды подграфов

На текущем этапе работы был определен такой вид графа(рис.3)

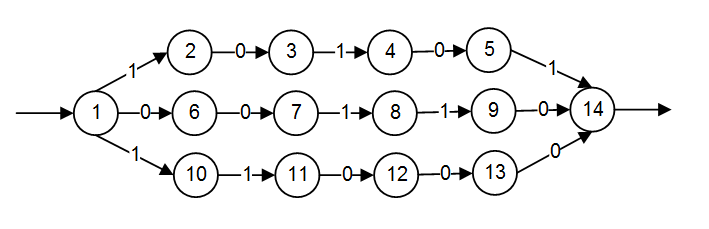
Алгоритм преобразования графа, путем сокращения его дуг и вершин

Рисунок 3 – K-вырожденный ациклический граф двухполюсник

Пояснение: K-вырожденный ациклический граф двухполюсник

K-вырожденный - в графе есть k параллельных путей

ациклический - в графе отсутствуют циклы

двухполюсник - имеет 1 начальную и 1 конечную вершину

Предлагается разработать метод анализа графов с целью выделения таких подграфов, поскольку для них очевиден простой алгоритм построения регулярного выражения. Так, для этого графа регулярное выражение =10101v00110 v11000

Выводы

Оптимизация алгоритма построения регулярного выражения по помеченному графу является актуальной на сегодняшний день.

В данной магистерской работе будут исследоваться различные виды подграфов, а также оптимальные пути их сокращения. В рамках проведенных исследований выполнено:

1. Проанализирован алгоритм предложенный Ногиной Н.В.

2. На основании вышеуказанного алгоритма были осуществлены ручные просчеты на разных видах графов.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2015 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список источников

  1. Ногина Н.В., Грунский И.С. - Синтез регулярного выражения языка,порожденного помеченным графом,методом его локальной редукции, 2012.
  2. Хопкрофт Д. Введение в теорию автоматов, языков и вычислений / Д. Хопкрофт, Р. Мотвани, Д. Ульман. – М.: Издательский дом «Вильямс», 2002. – 528 с.
  3. Кристофидес, Н. Теория графов: алгоритмический подход / Н. Кристофидес. – М.: Мир, 1978. – 430 с.
  4. Ахо А. Построение и анализ вычислительных алгоритмов / А. Ахо, Дж. Хопкрофт, Дж. Ульман. – М.: Мир, 1979. – 536 с.
  5. Батищев Д.И. Многоуровневая декомпозиция гиперграфовых структур / Батищев Д.И., Старостин Н.В., Филимонов А.В. // Прилож. к журналу «Информационные технологии» №5(141). – М.: Новые технологии. – 2008. – 32 с.
  6. Ногина Н.В. Построение кратчайшего пути в помеченном графе при помощи локальной редукции графа / Н.В. Ногина, А.В. Билык // Сучасна інформаційна Україна: інформатика, економіка, філософія: матеріали доповідей конференції, 26 квітня 2012 року. – Донецьк, 2012. – 316 с. – С. 76-79.
  7. Бєлов В.Теорія графів / Бєлов В.– М. : Питер,1968. – 304 с.
  8. Полат Е.С. Новые педагогические и информационные технологии / Полат Е.С. – М. : Akademia, 1999. – 401с.
  9. Кузнєцов О.П. Дискретная математика для инженера / Кузнєцов О.П. – М. : Энергоатомиздат, 1988. – 703 с.
  10. Оре О. Теорія графів / Оре О. – М. : Наука, 1980. – 340 с.
  11. Смольяков Е.Р. Введение в теоpию гpафов / Смоляков Е.Р. – М. : МГТУ, 1992. – 705 с.
  12. Hечепуpенко М.И. Алгоpитмы и пpогpаммы pешения задач на гpафах и сетях / Hечепуpенко И.М. – М. : Hаука, 1990. – 202 с.
  13. Романовский И.В. Алгоpитмы pешения экстpемальных задач / Романовский И.В. – М. : Hаука, 1977. – 506 с.
  14. Землянухин В.Н. Задачи оптимизации на графах / В.Н. Землянухин, Л.Н. Землянухина. – М. : Наука, 2009. – 677 с.
  15. Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение / В.А. Евстигнеев, В.Н. Касьянов. – М. : Наука, 1999. – 266 с.
  16. Новиков Ф.А. Дискретная математика / Новиков Ф.А. – М. : Питер, 2001. – 301 с.
  17. Алгоритмы на графах [Электронный ресурс] - http://www.chasolimp.de/alggraph_prac.htm